Планувальні схеми вуличної мережі міста

Вулична мережа міста – один з найбільш стабільних його елементів, тому повинна бути розрахована на дуже тривалий період використання без істотних перебудов, що обходяться надто дорого.

Вулиці й дороги утворюють на плані міста мережу наземних шляхів сполучення. Якщо з вулично-дорожньої мережі кожного міста виділити магістральні напрямки, що є, власне кажучи, основою міського плану, то чітко виявляється принципова геометризована схема планування кожного міста.

Існує вісім принципових геометризованих схем, що охоплюють все різноманіття міських планувальних структур:

· вільна;

· радіальна;

· радіально-кільцева;

· трикутна;

· прямокутна;

· прямокутно-діагональна;

· гексагональна;

· комбінована.

Вільна схема (рис. 2.3) характерна для старих міст із невпорядкованою вулично-дорожньою мережею. Уся мережа складається з вузьких кривих вулиць із змінною шириною проїзної частини, що нерідко виключає рух у двох напрямках. Реконструкція такої мережі вулиць, як правило, зв'язана з руйнуванням існуючої забудови. Для сучасних міст ця схема непридатна і може бути залишена тільки в заповідних частинах міста.

Радіальна схема (рис 2.4) зустрічається в невеликих старих містах, тому що при цій схемі дуже ускладнені зв'язки між периферійними районами, що викликають значний перепробіг і перевантаження центра. Вона застосовується в основному в малих населених пунктах, що характеризуються незначною дальністю пересувань і низкою щільністю машинопотоків.

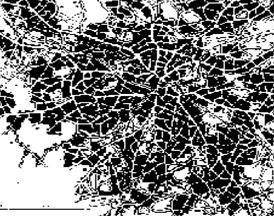
Рис. 2.3 - Вільна схема

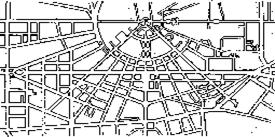
Рис. 2.4 - Радіальна схема

Радіально-кільцева схема (рис. 2.5) вуличної мережі характерна для значних і великих міст і має два принципово різних види магістралей – радіальні й кільцеві. Радіальні магістралі є найчастіше продовженням автомобільних доріг і служб для глибокого введення транспортних потоків у місто, для зв'язку центра з периферійними районами й окремими районами між собою. Кільцеві магістралі – це насамперед, розподільні магістралі, що з'єднують радіальні і забезпечують перевезення транспортних потоків з однієї радіальної магістралі на іншу. Вони служать також для транспортного зв'язку між окремими районами, розташованими в одному поясі міста. Прикладом такого планування є Москва.

Радіально-кільцева схема вуличної мережі має найменший коефіцієнт непрямолінійності –1,05-1,1.

Трикутна схема (рис. 2.4) не одержала великого поширення, тому що гострі кути, утворені в пунктах перетину елементів вулично-дорожньої мережі, створюють значні труднощі і незручності при освоєнні та забудові ділянок. Елементи трикутної схеми можна зустріти в старих районах Лондона, Парижа, Берна та інших міст.

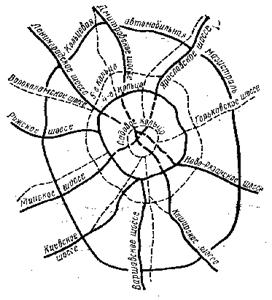
Рис. 2.5 - Радіально-кільцева схема

Прямокутна схема (рис. 2.7) дуже поширена і притаманна, головним чином молодим містам чи відносно старим, що будувалися за єдиним планом. До числа таких міст відносяться Санкт-Петербург, Алма-Ата, ряд американських міст. Перевагами прямокутної схеми є відсутність чітко визначеного центрального ядра і можливість рівномірного розподілу транспортних потоків по всій території міста. Недоліки цієї схеми – велика кількість завантажених перехрещень, що ускладнюють організацію руху і збільшують транспортні витрати, великі перепробіги автомобілів. Коефіцієнт непрямолінійності –1,4-1,5.

Прямокутно-діагональна схема (рис 2.8) є розвитком прямокутної схеми. Вона містить у собі діагональні й хордові вулиці, що пробиваються в існуючій забудові по найбільш завантажених напрямках. Ця схема трохи поліпшує транспортну характеристику вуличної мережі міста, але створює нові проблеми: перетинання міста по діагоналі викликає появу складних перехрещень з п'ятьма і шістьма вулицями, що вливаються. Коефіцієнт непрямолінійності для таких схем складає 1,2-1,3.

Рис.2.6 - Трикутна схема

Гексагональна схема (рис. 2.9) – це схема, в основі якої лежить комбінація шестикутників. У цій схемі виключається утворення складних вузлів на пересіченнях магістральних вулиць, а також протяжних прямолінійних напрямків, що створюють умови для швидкісного руху транспорту. Схема не має великого поширення.

Комбінована схема (рис. 2.10) характерна для великих і значних історично сформованих міст. Тут нерідко зустрічаються в центральних зонах вільна, радіальна чи радіально-кільцева структура, а в нових районах вулично-дорожня мережа розвивається за прямокутною чи прямокутно-діагональною схемою.

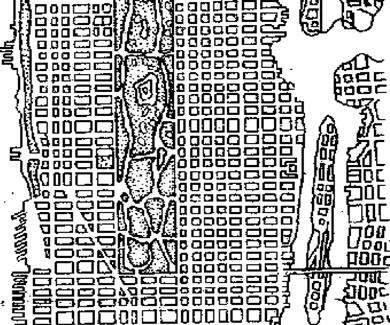
Рис. 2.7 - Прямокутна схема.

Рис. 2.8 - Прямокутно-діагональна схема.

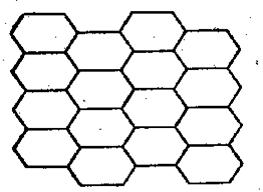
Рис. 2.9 - Гексагональна схема.

У чистому вигляді всі розглянуті схеми вуличної мережі в сучасних великих містах зустрічаються мало. По мірі розвитку міста, його транспортної системи планувальна схема вулиць все більше здобуває вигляд спочатку радіальної схеми, потім, після будівництва обхідних доріг по границях міста і вулиць, що оперізують центр міста, радіально-кільцевої. У межах одного району найчастіше зберігається прямокутна схема вулиць.

Рис.2.10 - Комбінована схема.

Дата добавления: 2014-10-15