Истечение жидкости из отверстий и насадков

Лекция 6.

5. Истечение жидкости из малого отверстия в тонкой стенке, при постоянном напоре.

Отверстие считается малым, если его размер по высоте значительно меньше, чем напор, не более чем 0,1Н.

Тонкая стенка – это стенка с острой кромкой. Считается, что жидкость, истекающая из такого отверстия, преодолевает только местные сопротивления.

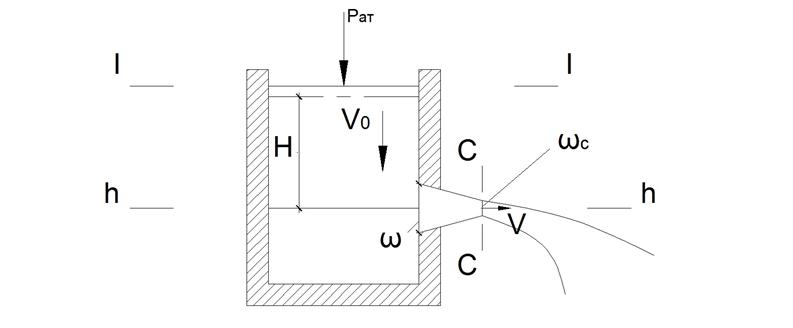
Рис. 39. Схема истечения жидкости из малого отверстия в тонкой стенке при постоянном напоре.

При истечении струя на некотором расстояния образует сжатие сечения от к . При этом - коэффициент сжатия.

Сжатие бывает полное, когда прослеживается по всему периметру, и неполное, когда отверстие примыкает к какому-нибудь препятствию. В том месте струя не имеет бокового сжатия. Например, отверстие примыкает к стенке или к дну сосуда.

Сжатие бывает совершенным, когда отверстие находится на значительном расстоянию от стенок и дна сосуда, и последние не приводят к деформации струи. И не совершенным, когда имеет место определенная деформация

m>3а – условие совершенного сжатия, где

а – размер отверстия;

m – расстояние от стенок до дна.

Составим уравнение Бернулли относительно плоскости n-n, проходящей через центр тяжести отверстия в тонкой стенке для сечений 1-1 и C-C:

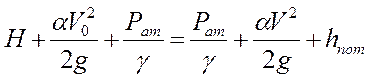
Здесь h_пот - потери напора на вход в отверстие.

(сечение резервуара слишком велико)

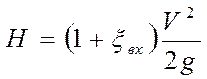
- коэффициент скорости истечения из отверстия. Тогда скорость истечения из отверстия:

(1)

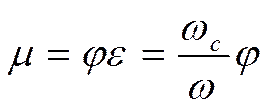− коэффициент расхода истечения из отверстия. Тогда расход, истекающий из отверстия:

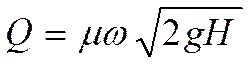(2)

В справочниках приводятся значения j, m и x_вх, в зависимости от формы отверстия и схемы работы отверстия (затопленное или нет).

Скорость истечения из отверстия в тонкой стенке:

Расход истечения из отверстия в тонкой стенке:

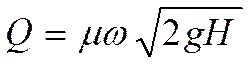
6. Истечение из отверстия в тонкой стенке при переменном напоре.

Рис. 40. Истечение жидкости из малого отверстия в тонкой стенке при переменном напоре.

Здесь 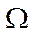- площадь свободной поверхности резервуара.

Учитывая, что напор над отверстием в процессе истечения изменяется от Н₁ до Н₂, выражения для скорости истечения и расхода из такого отверстия будут аналогичны выражениям (1) и (2), но со значением средней величины напора Н_ср:

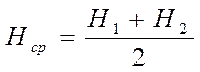
Эти выражения пригодны для приближенных расчетов для истечения из резервуаров постоянного сечения, например, цилиндрических.

Время опорожнения резервуара при истечении с напорами над отверстием от Н₁ до Н₂:

При Н₂=0 , где W - объем резервуара.

Если имеются два резервуара с глубинами Н₁ и Н₂ и свободными поверхностями и, 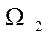, которые соединены тонкой стенкой с отверстием площадью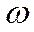, тогда время уравнивания их уровней:

3. Истечение из большого отверстия в тонкой стенке при постоянном напоре.

Отверстие считается большим, если его высота а>0,1Н.

Здесь

Рис. 41. Истечение жидкости из большого отверстия при постоянном напоре.

z – расстояние элементарной полоски от поверхности жидкости;

b – ширина отверстия;

а – высота отверстия;

dQ – элементарный расход сквозь элементарное сечение.

.

Интеграл от элементарных расходов – это расход через всё сечение:

(3)

Формула (3) используется для выведения расчетной формулы расхода водослива.

4. Истечение жидкости из насадков.

Насадки – это специальные гидравлические устройства для формирования струи, которая вытекает из какого-нибудь резервуара или трубопровода.

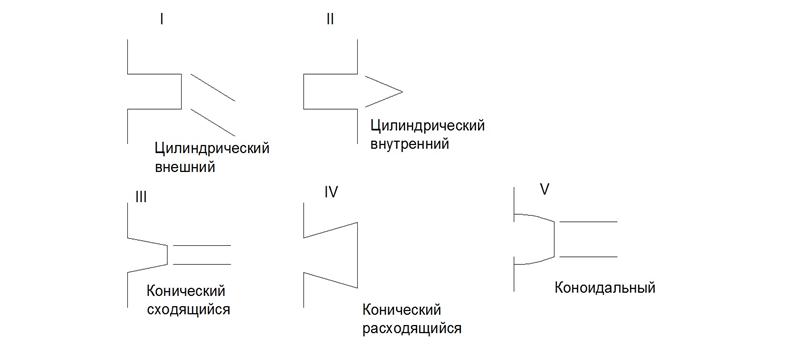
Рис. 42. Основные гидравлические типы насадков.

Процесс истечения жидкости из насадка.

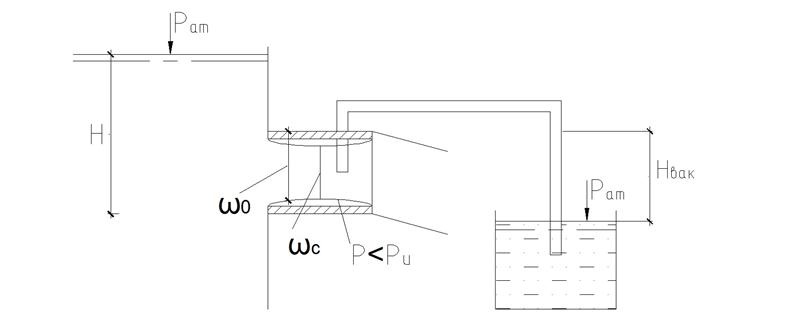
Рис. 43. Принцип работы насадка.

Рассматривается истечение из насадка при постоянном напоре Н. В процессе истеченияния в насадке достаточной длины образуется сжатое сечение, которое успевает возобновиться к выходу жидкости наружу. В области сжатого сечения в насадке образуется вакуум, поскольку давление в нем меньше атмосферного:

h_вак=0,75Н

Эта зависимость справедлива при Н£7м, иначе возникает срыв вакуума и насадок начинает действовать как отверстие в тонкой стенке. Сжатое сечение, как бы выталкивается из насадка наружу большим напором Н.

Для номальной работы насадка (с восстановлением сжатого сечения) длина его должна быть не меньше, чем 3¸4 диаметра.

Поскольку сжатое сечение в насадке восстанавливается до нормального, то значение коэффициентов скорости и расхода уравниваются, то есть μ_н=εφ=1.

Расход из насадка: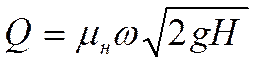

Поэтому расход через насадок больше, чем через отверстие того же диаметра.

Потери напора в насадке тоже учитываются только местные, а значение коэффициентов m приведены в справочниках для разнообразных насадков.

Области применения насадков, приведенных выше, в начале темы:

1 – используется для формирования струи. Коэффициент расхода m_н больший, чем у отверстий:

m_н=0,82 >m₀=0,62, а расход больше в 1,32 раза.

2 – используется в особых конструкциях, когда нельзя использовать внешний насадок при дефиците места. Обладает большим сопротивлением на входе m=0,77.

3 - формирует струю с высокой выходной скоростью (пожарный шланг) m=f(q), где q - угол конусности. m_мах=0,94 при q=13°.

4 – дает низкие выходные скорости. Используются для выпусков с малыми скоростями, которые не размывают почву, для всасывающих труб насосов. Максимальное значение m=0,5 при q=5-7°.

5 – обладает малым гидравлическим сопротивлением и высокой выходной скоростью, Максимальное значение m=0,97. Используется для разбрызивающих сопел градирен.

Дата добавления: 2014-10-15