Лекция 5

Местные гидравлические сопротивления.

Местные сопротивления – это сопротивления препятствий, обтекаемых жидкостью. При наличии таких препятствий происходит отрыв потока и образование вихревых зон. На деформацию линий тока в этих зонах теряется часть энергии потока.

Потери напора на местных сопротивлениях подразделяются:

6. Потери, связанные с изменениями сечения трубопровода (внезапное или медленное сужение или расширение);

7. Потери, связанные с изменением направления движения потока (угольники, отводы);

8. Потери, связанные с протеканием жидкости сквозь арматуру (вентили, задвижки, диафрагмы, обратные клапаны и тому подобное);

9. Потери, связанные с разделением или слиянием потока (тройники, крестовины);

10. Потери на сварных стыках трубопроводов.

Все местные сопротивления могут быть определены опытным путем как разность показаний пьезометров или манометров (смотри лекцию 4).

Путем расчета все местные сопротивления определяются по формуле Вейсбаха:

Вообще, задача заключается в том, чтобы определить коэффициент местного сопротивления . Большинство коэффициентов определяется по эмпирическим формулам. Небольшая группа коэффициентов определяется теоретически на основании теоремы Борда-Карно.

Потери напора при внезапном расширении трубопровода (теорема Борда-Карно).

Потери напора при внезапном или резком расширении потока равняются скоростному напору потерянной скорости

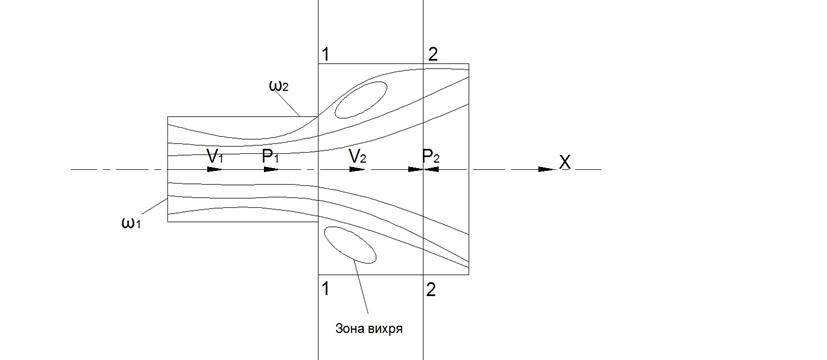
Рис. 27. Потери напора на «классическом» гидравлическом сопротивлении – «внезапном расширении трубопровода»

Применим «Теорему импульсов» классической механики к участку жидкости между сечениями 1-1 и 2-2.

Проекцияна произвольно взятую координатную (ось трубопровода) приращения количества движения равняется сумме импульсов внешних сил, действующих на рассматриваемый участок, за определенное время (пусть время τ=1с):

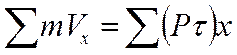
Из внешних сил в уравнение включаем только силу гидродинамического давления Р, потому что силу трения на малом участке не учитываем.

- сумма сил в направлении движения потока – сумма сил давления.

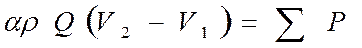
Разделим это последнее уравнение на 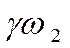и примем a=1

*

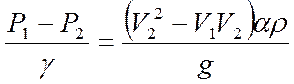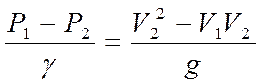
Составим уравнение Бернулли для сечений 1-1 и 2-2 и

Подставим из уравнения * его часть::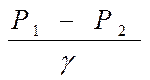

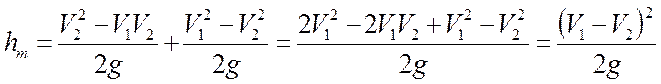
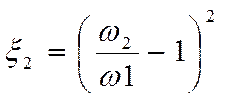
Потери напора в диффузорах (трубках, которые медленно расширяются).

Диффузор характеризуется углом раскрытия или конусностью.

Рис. 28. Потери напора на плавном расширении потока (диффузоре)

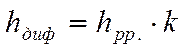
Здесь hдиф - потери напора в диффузоре;

- коэффициент местного гидравлического сопротивления диффузора;

hрр - потери напора на внезапном расширении потока;

k - коэффициент смягчения (уменьшения значения).

Потери напора в диффузоре будут меньшими, чем при внезапном расширении потока, поскольку вихревые области медленно сглаживаются.

Потери напора в диффузоре определяются как для внезапного расширения, но с умножением на коэффициент смягчения k <1, который зависит от угла конусности a.

Значения коэффициентов приведены в справочниках по гидравлике.

- максимальное снижение a.

Рис. 29. Область оптимального значения коэффициента смягчения k

Потери напора при внезапном или резком сужении потока.

Рис. 30. Определение потерь напора на «внезапном сужении» потока.

Частицы жидкости, которые входят в узкое сечение, стремятся сберечь свою траекторию по инерции и формируют так называемое сжатое сечение ₋ ω_с.

Потери напора возникают при расширении сечения от ω_с до ω₂:

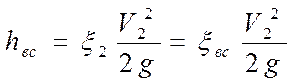
Здесь - степень сжатия струи, или коэффициент сжатия.

- сжатое сечение измерить очень сложно, поэтому в расчетах используют эмпирическое (опытно найденное) значение, указанное в справочниках.

При 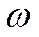_1>> 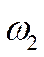=0.611 (истечение из резервуара) =0,42

Потери напора в медленно суживающихсяся трубах (конфузорах).

Рис. 31. Потери напора на медленном сужении потока (конфузоре)

Потери напора определяются также, как для внезапного сужения, но с умножением на коэффициент смягчения, который меньше единицы. В соответствии углу конусности α₁ для k₁<1 справочниках приводится графическая или табличная зависимость.

Рис. 32. Область оптимального значения коэффициента смягчения k₁

Значения для конфузоров приведены в справочниках, в зависимости от соотношения большего и меньшего сечений.

Потери напора в отводах, коленах, угольниках.

Колена образуют тем большие гидравлические сопротивления, чем более резок их поворот, то есть чем меньший их радиус закругления R. Колено считаетсяется острым, если r=R. Для такого колена 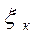=1. Для более закругленных колен и отводов в справочниках приведены значения .

Рис. 33. Потери напора в коленах, отводах, угольниках.

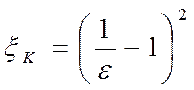, где в зависимости от соотношения.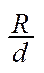

Потери напора в диафрагмах.

Диафрагма – это искусственное образованное внезапное сужение потока в трубопроводах. Она существует для гашения напора или для измерения расхода (измерительная диафрагма). В последнем случае учитывается связь потерь напора с величиной скорости и расхода в трубопроводе.

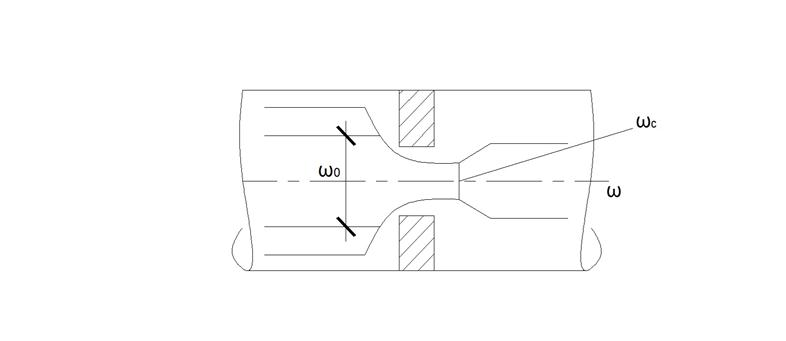
Рис. 34. Потери напора в диафрагмах.

,

где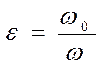

Значение и приведены в справочниках.

Потери напора в тройниках и крестовинах(крестах)

Существуют две группы тройников – нагнетающие (1) и всасывающие (2) или приливные и втяжные.

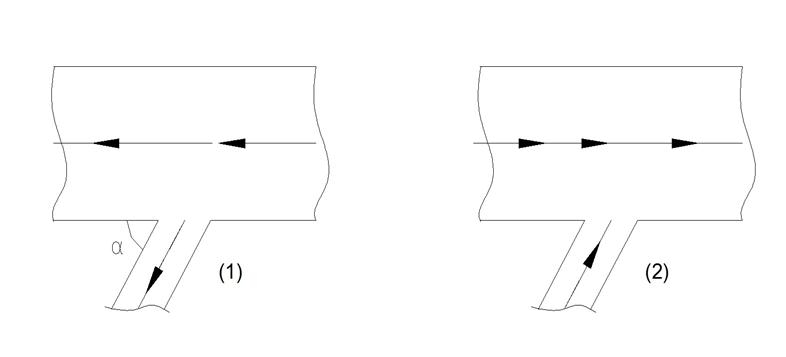
Рис. 35. Схемы к определению коэффициентов местных сопротивлений для тройников.

В тройниках отличают магистраль и ответвление.

Поворот потока в них может происходить только на угол ³90°.

Потери напора зависят от схемы работы тройника в потоке, от угла между магистральными направлением и ответвлением a, от соотношения их диаметров. 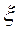и h_m зависят, к какой скорости их отнести: к магистральной или на ответвлении, до или после ответвления. Все возможные схемы приведены в справочниках.

Потери напора на задвижках и вентилях.

Потери напора на задвижках и вентилях возникают в результате уменьшения сечения трубопровода. Как для внезапного сужения потока.

Рис. 36. Потери напора в задвижках и вентилях.

Значения 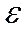приведены в справочниках, в зависимости от степени открытия задвижки или вентиля. Но полностью открытая арматура образует сопротивление своим клапаном. Для полностью открытой задвижки рекомендуется брать = 0,1-0,2, а для полностью открытого вентиля =5-10.

Потери напора на сварных стыках.

Опыты показали, что влияние стыков можно рассматривать как увеличение коэффициента гидравлического трения l.

Рис. 37. Влияние стыков труб на увеличение гидравлического

трения.

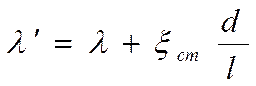
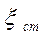- индивидуальное сопротивление стыка (по справочнику).

l - коэффициент Дарси без стыков.

’- то же со стыками.

Зависимость коэффициентов местных сопротивлений от числа Рейнольдса.

Рис. 38. Определение коэффициентов местных гидравлических сопротивлений в не квадратичной области турбулентного режима.

Для больших чисел Рейнольдса, соответствующих квадратичной области гидравлического сопротивления, зависимость 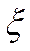=f(Rе) исчезает. При малых числах Rе – зависит значительно. Значения 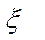в справочниках вычислены для квадратичной области сопротивления. Для перехода в другие области (гидравлически гладких труб, переходную) есть формула:

, где

А – экспериментально полученная величина, которая приводится в зависимости от значения Rе_.

Взаимное влияние местных сопротивлений.

При гидравлическом расчете коэффициенты местных сопротивлений можно складывать, когда они находятся на участке на расстоянии одного от одного, более чем расстояние влияния.

Расстояние влияния – это расстояние, на котором эпюра скоростей, деформированная предыдущим местным сопротивлением, возобновляет форму. Расстояние влияния l определяется из соотношения:

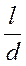- калибр трубы. Для инженерных расчетов допускается =20¸30.

В ином случае коэффициенты ξ в расчетах также складываются, но сумма умножается на коэффициент запаса >1, который учитывает снижение точности расчетов.

Дата добавления: 2014-10-15