Гидравлические сопротивления. Два режима движения жидкости. Определение потери напора по длине

Лекция 4.

Для идеальной жидкости все задачи решаются системой двух уравнений.

Для реальной жидкости, которая имеет свойство вязкости, в систему добавляется 3-есть уравнение, и система обретает вид:

С помощью этой системы решаются все гидродинамические инженерные задачи. Аналогично – аэродинамические.

Существуют две группы потерь напора:

Первая – на трение или по длине.

Вторая – на местные сопротивления – при протекании жидкости через какого-нибудь рода препятствия (колена, отводы, тройники, задвижки и тому подобное).

Оба вида потерь напора могут быть найдены опытным путем – это подходит для существующих водоводов и других систем коммуникаций. Например, на существующем водоводе потери напора на участке 1-2.

Составим уравнение Бернулли для потока реальной жидкости для сечений 1-1 и 2-2.

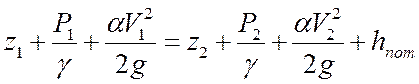
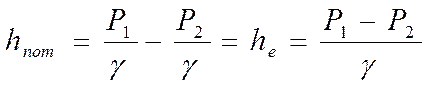, где d=const

V=const, = const

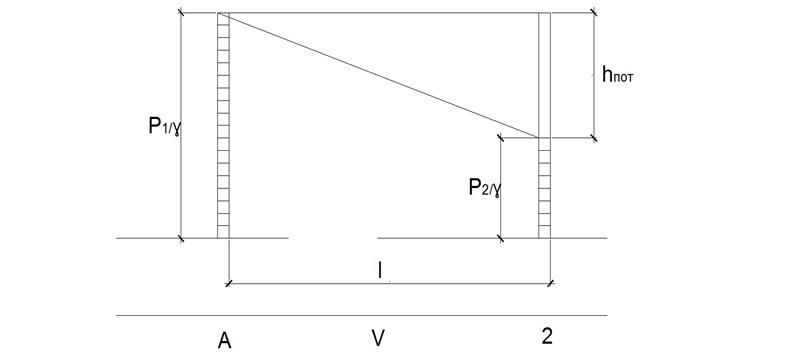
Рис.21. Определение потерь на местных сопротивлениях опытным путем.

Таким же образом пьезометры устанавливаются до и после местного сопротивления и определяют потери напора h_m на местном сопротивлении.

Рис.21. Определение потерь на местных сопротивлениях опытным методом.

при =1

Потеря напора жидкости при ее движении состоит из суммы потерь на трение и на местные сопротивления:

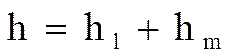
Путем расчета, для проектирования, потери напора на гидравлическое трение определяются, в общем случае по формуле Дарси-Вейсбаха:

(1)

Здесь 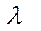- коэффициент гидравлического трения, безразмерная величина (коефициен Дарси).

l - длина трубопровода, м.

d - диаметр трубопровода, мм.

- средняя скорость потока, м/с, на участке.

Местные потери напора определяются по формуле Вейсбаха:

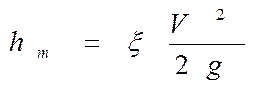
Здесь - коэффициент местного сопротивления, безразмерная величина, которая зависит от вида местного сопротивления.

- средняя скорость на участке за местным сопротивлением, м/с.

Коэффициенты 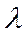и зависят от многих факторов, главным из которых является режим движения жидкости и шероховатость стенок трубопровода.

Два режима движения жидкости.

В 1883 году английский ученый Рельнольдс доказал наличие 2-х режимов движения частиц жидкости. Сквозь стеклянную трубку пропускали воду со средней скоростью V.

1 – бак постоянного напора.

2 – бачок с окрашенной жидкостью.

3 – стеклянная трубка.

4 – перливная трубка.

5 – регулирующие вентили.

6 – тонкая трубочка с заостренным струенаправляющим концом.

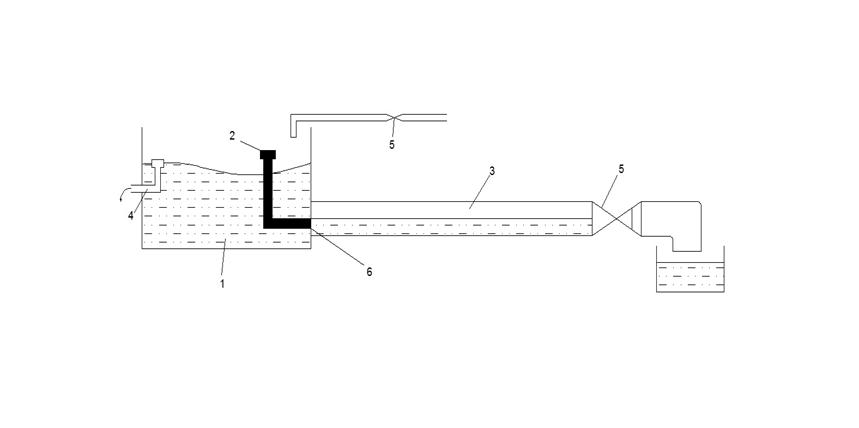
Рис. 22. Опыт Рейнольдса по определениию двух режимов движения

жидкости.

При малых скоростях V движения воды линия окрашенной жидкости не перемешивается с остальной водой в трубке 3. При некоторой критической скорости V_кр струйка окрашенной жидкости размывалась в контуре и перемешивалась с остальной водой. То есть, можно сказать, что движение частиц жидкости в первом случае имело параллельноструйный характер, а во втором случае – хаотический.

Первый режим движения жидкости называется ламинарным (параллельноструйним), а второй – турбулентным (беспорядочным).

Опыты показали, что вид режима зависит от безразмерного параметра − критерия Рейнольдса Re, либо числа Рейнольдса.

Здесь V - средняя скорость потока в трубе, м/с;

d - диаметр трубы, м;

- кинематическая вязкость, м²/с.

Число Рейнольдса, при котором движение ламинарное переходит к турбулентному, называется критическим.

При этом соответствующая скорость называется критической:

Практически, число находится в пределах 1000-4000.

Для открытых русел (безнапорное движение):

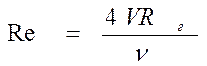
Здесь R_г - гидравлический радиус, м. Практически это число равняется 300-500.

Дата добавления: 2014-10-15