Уравнение Бернулли для потока реальной жидкости и элементарной струйки. Пьезомерический и гидравлический уклоны. Водомер Вентури

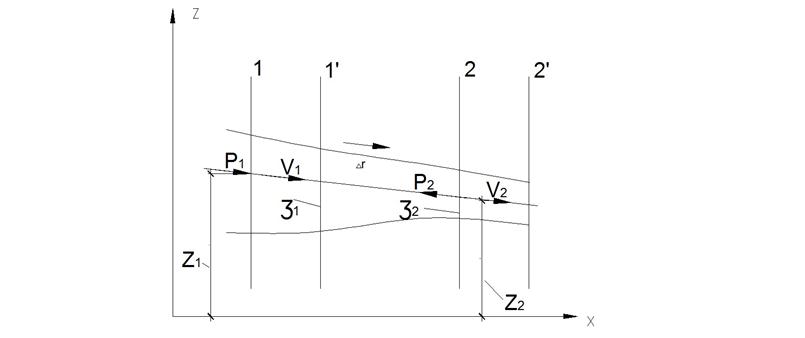
Рис. 17. К выводу уравнения Бернулли для потока реальной жидкости.

Рассмотрим поток реальной жидкости с плавноизменяющимся движением.

Выберем два произвольных сечения 1-1 и 2-2, которые нормальны к оси потока, и рассмотрим участок потока, заключенный между ними. Обозначим скорости в этих сечениях V₁ и V₂; площади живых сечений ω₁ и ω₂; гидравлические давления в центрах тяжести этих сечений р₁ и р₂; расстояния до плоскости сравнения О-О − Z₁ и Z₂.

Применим к участку потока, замкнутому между сечениями 1-1 и 2-2, закон сохранения енергии. За время 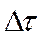частицы жидкости перейдут из положения 1-1 в положение 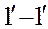, а из положения 2-2 – в положение 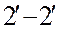. При этом будут пройдены пути V₁ * 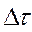и V₂*.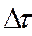

Сквозь сечение 1-1 за время 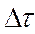пройдет объем жидкости Q_1*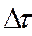, а это же время сквозь сечение 2-2 пройдет объем жидкости Q₂*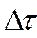. Найдем количество энергии, внесенной потоком в рассматриваемый участок, за время 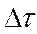через сечение 1-1.

Объем жидкости W₁ обладает массой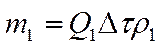

Потенциальная энергия этого объема:

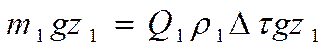
А кинетическая энергия этого же объема::.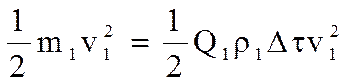

Рассматриваемый объем обладает также энергией давления.

Представим, что в сечении 1-1 есть поршень, движущийся со скоростьюV₁ в направлении сечения 2-2. Этот поршень за время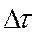 пройдет путь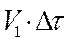. Сила давления на поршень P₁.Тогда работа поршня равна: 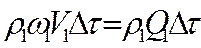. Потенциальная энергия объема,:

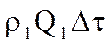
Тогда общее количество энергии, внесенной потоком в рассматриваемый участок за время 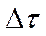сквозь сечение 1-1 будет равняться: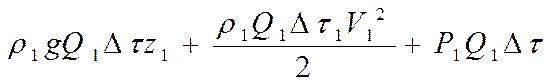

Аналогично, суммарная энергия потока, вынесенная потоком сквозь сечение 2-2 равняется:

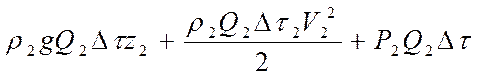
По закону сохранения энергии суммарная энергия, внесенная сквозь сечение 1-1 при установившемся движении, должна равняться суммарной энергии, вынесенной сквозь сечение 2-2 с учетом затрат энергии на преодоление гидравлических сопротивлений на рассматриваемом участке.

Затраченную энергию на преодоление сопротивлений можно передать в виде произведения веса рассматриваемого объема на некоторую высоту h_{пот 1-2} – в виде потенциальной энергии потерь высоты или напора:

тогда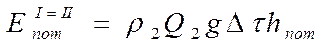

Согласно с уравнением постоянства расходов Q₁=Q₂=const.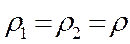для несжимаемой однородной жидкости.

Поэтому можно приравнять оба уравнения для сечений 1-1 и 2-2:

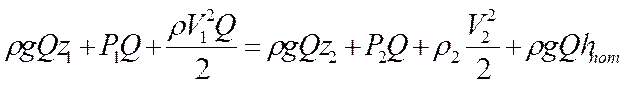
Отнесем оба уравнения к весу жидкости 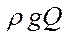и получим:

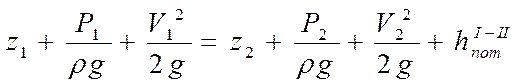
Это выражение является уравнением БернулЛи для потока реальной жидкости.

Здесь Z – расстояние центра тяжести рассматриваемого сечения до плоскости сравнения; Р – давление в центре тяжести сечения; V – средняя скорость в сечении; h_пот – удельная энергия, затраченная на преодоление сопротивлений от начального сечения до рассматриваемого.

Если учитывать неравномерность распределения скоростей по живому сечению потока, то уравнение Бернулли получает конечный обобщенный вид:

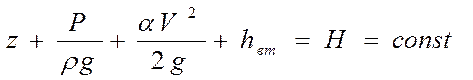(1)

Здесь a - коэффициент Кориолиса, учитывающий влияние неравномерности распределения скоростей по сечению на удельную кинетическую энергию потока. Коефициент a изменяется в пределах 1-2, причем его приблизительное значение можно брать равным 1.

Сумма двух первых слагаемых уравнения 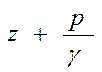является пьезометрическим напором (сравним с основным уравнением гидростатики);

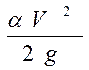- скоростной или динамический напор;

h_пот – утраченный или потерянный напор;

H – полный гидродинамический напор.

Геометрическое содержание уравнения Бернули.

Все слагаемые уравнения (1) выражаются в единицах длины.

Z – геометрическая высота или высота положения;

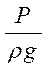или 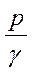- пьезометрическая высота;

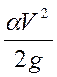- или высота гидродинамического давления;

h_пот - высота потерь напора или потери напора.

При установившемся движении жидкости сумма 4-х высот (высоты положения, пьезометрической высоты, высоты гидродинамического или скоростного напора и высоты потерь напора) остается неизменной вдоль потока.

Энергетическое содержание уравнения Бернулли.

Все четыре слагаемого уравнения (1) являются удельными энергиями (отнесенными к весу жидкости) потока.

При установившемся движении жидкости сумма 4-х удельных энергий (энергии положения, энергии гидродинамического давления, кинетической энергии и потерянной энергии) остается неизменной вдоль потока.

Полная энергия (в виде напора) в потоке измеряется трубкой Питто (динамической трубкой), которая имеет форму перевернутой буквы Г, направленной навстречу потоку. Пьезометрический напор 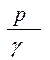измеряется пьезометрической трубкой (с гладким концом).

ГИДРАВЛИЧЕСКИЙ И ПЬЕЗОМЕТРИЧЕСКИЙ УКЛОНЫ

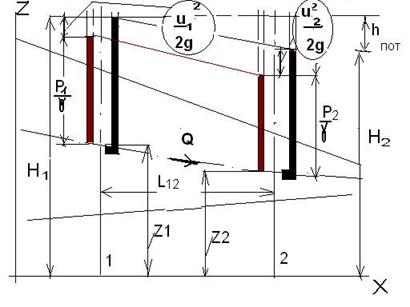
Рис. 18. Распределение напоров в потоке при определении гидравлического и пьезометрического уклонов.

Соединив уровни жидкости в пьезометрических трубках, получим линию пьезометрического напора или линию удельной потенциальной энергии 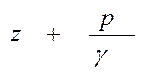. Падение пьезометрического напора на единицу длины L называется пьезометрическим уклоном:

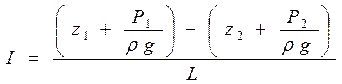
Пьезометрический уклон может быть как положительным, так и отрицательным.

Падение линии полного напора на единицу длины называется гидравлическим уклоном i:

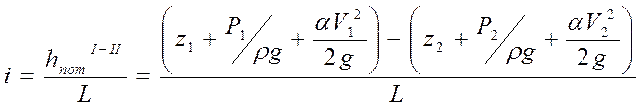
Гидравлический уклон, согласно закона сохранения энергии, может быть исключительно положительным в направлении потока.

Уравнение Бернулли для элементарной струйки реальной жидкости для какой-либо точки, где жидкость движтся с местной скоростью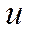

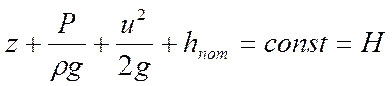
Уравнение Бернулли для идеальной жидкости будет отличаться от выражений (1) и (2) отсутствием слагаемого, соответствующему удельной энергии потерь напора (то есть без h_пот).

Уравнение Бернулли справедливо для идеального и реального газа, Приводится в форме давлений. Для струйки идеального газа:

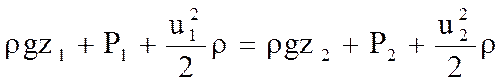
Для потока реального условно несжатого газа в расчетах часто не учитывают разность высотных отметок Z₁ и Z₂, а также пренебрегают скоростными давлениями, ничтожно малыми, по сравнению с потенциальными. В итоге выходит расчетная формула для определения потерь давления газа Р_пот при следовании по трубопроводу:

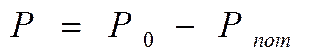
Здесь Р₀- начальное давление в трубопроводе, Р – конечное давление в пункте приема газа.

Измерения давления газа производят с помощью манометров, Для сжатого газа уравнения Бернулли изучается в курсе аэродинамики.

Дата добавления: 2014-10-15