Лекция 2. Давление жидкости на плоские и криволинейные поверхности

Давление жидкости на плоские и криволинейные поверхности.

При определении силового действия жидкости на твердую поверхность обычно решают две задачи: определяют величину равнодействующей сил гидростатического давления и находят точку ее приложения, которая имеет название: центр давления.

d) Сила давления жидкости на плоское горизонтальное дно.

Точка приложения этой силы – центр тяжести площадки . Если определим силу гидростатического давления Р на площадку как , то , где Р_изб – сила избыточного давления.

e) Сила давления жидкости на произвольно ориентированную плоскую поверхность.

Рис. 9. Вывод величины и точки приложения силы гидростатического давления на плоскую поверхность.

Здесь: С- центр тяжести

D- центр давления

В пределах площадки 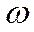выберем бесконечно малую площадку dω – на глубине h на расстоянии X по оси Z и Z по оси X.

h_c – расстояние от свободной поверхности жидкости до центра С тяжести площадки – глубина погружения центра тяжести.

h_d – глубина погружения точки, в которую приложена равнодействующая силы гидростатического давления или глубина погружения центра давления.

X_c, X_д; Z_c, Z_д – координаты указанных центров.

Сила гидростатического давления, действующая на элементарную площадку dω:

Полная сила гидростатического давления на площадку :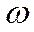

(2)

Поскольку на свободную поверхность давление действует постоянное по величине давления, то интеграл от константы равен:

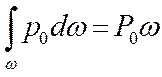
Второй интеграл:

Здесь

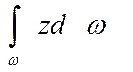- статический момент площадки относительно оси ох - поэтому =

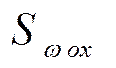
Подставив оба интеграла в выражение равнодействующей силы (2), получим:

Сила полного гидростатического давления на произвольно ориентованную плоскую поверхность равна произведению полного гидростатического давления в центре тяжести рассматриваемой площадки на величину этой площадки.

Координаты точки приложения силы полного гидростатического давления определяются как для равнодействующей параллельных сил - силы избыточного давления и силы внешнего давления на свободную поверхность:

Р₀ прикладывается в центре тяжести рассматриваемой площадки. Если_, открыта поверхность жидкости, то Р₀=Р_атм и сила Р₀ часто исключается из расчетов.

Определяем точку приложения (X_D, Z_D). Составляем уравнения моментов относительно оси ОХ на основании теоремы Вариньона (момент равнодействующей сил равняется сумме моментов всех составляющих сил относительно любой оси для тела, находящемся в состоянии механического равновесия):

, то есть

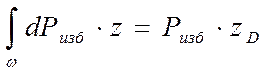где

dР_изб - элементарная сила избыточного давления на элементарную площадку dω на расстоянии Z от оси ОХ.

Р_изб – сила избыточного давления на всю площадку .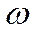

где h=zsina

Здесь - момент инерции площадки – относительно оси ox ‒

- центральный момент инерции – относительно оси, проходящей через центр тяжести С и параллельно оси Х:

Центр давления всегда находится ниже, чем центр тяжести.

Составим уравнение моментов относительно оси Z_D и получим координату X_D – точки приложения равнодействующей силы избыточного давления – центра давления.

Для площадок, симметричны относительно оси, параллельной оси ОХ, центр тяжести и центр давления расположены на одной вертикальной прямой, параллельной оси Z.

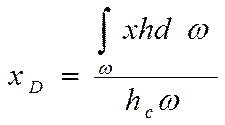
с) Давление жидкости на криволинейную поверхность.

Рис. 10. Сила гидростатического давления на криволинейную поверхность.

Выберем в среде жидкости, находящейся в состоянии покоя, произвольный объем W, ограниченный поверхностью S.

Силы гидростатического давления направлены по внутренним нормалям к граничной поверхности. Виделим криволинейную элементарную площадку d. На нее будет действовать сила полного гидростатического давления dP с проекциями dP_x, dP_y, dP_z. Тогда из уравнения (1) имеем:

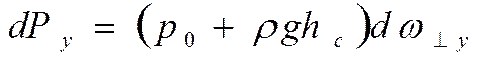
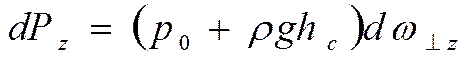
где - проекция площадки – на плоскость, перпендикулярную оси ОХ.

- перпендикулярную OY

- перпендикулярную OZ

Для проекции dP_z на плоскость, перпендикулярную оси OZ, выражение

Можно проинтегрировать и записать в виде:

, где W_ТД – объем жидкости, который

называется телом давления.

Тело давления – это объем жидкости, образованный рассматриваемой площадкой, отмеренный по нижний образующей криволинейной поверхности, а также ограниченный вертикальной поверхностью, установленной от границ этой криволинейной поверхности к свободной поверхности жидкости или ее продолжением. Если тело давления находится со смачиваемой стороны поверхности, оно считается отрицательным (перед формулой ставится минус), а если с несмачиваемой стороны -то позитивным (со знаком плюс).

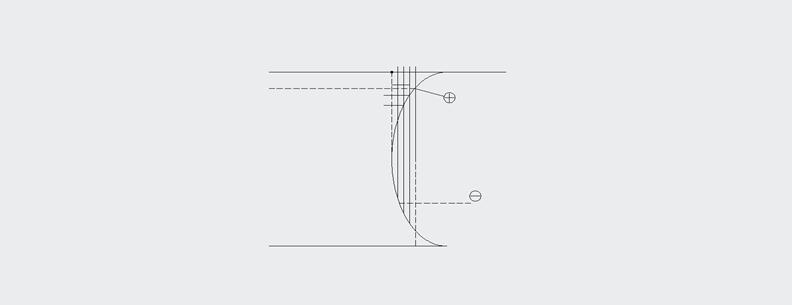
Рис. 11. Пример определения „тела давления”.

Для результирующей силы полного гидростатического давления на криволинейную поверхность получим выражения:

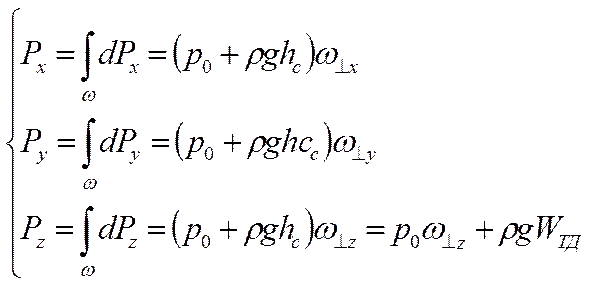
Для результирующей избыточного гидростатического давления на криволинейную поверхность имеем аналогичные выражения:

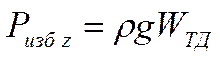
Направление вектору силы полного или избыточного гидростатического давления определяется углом a

или

Закон Архимеда.

На тело, погруженное в жидкость, действует сила гидростатического давления, или подъемная сила, которая равняется по величине веса жидкости, вытесненной телом. Она направлена вертикально вверх и проходит сквозь центр тяжести вытесненной жидкости. И называется Силой Архимеда.

На поверхность АВС действует сила

Рис.12. Закон Архимеда с точки зрения определения гидростатического давления на криволинейные поверхности.

На поверхность АDС действует сила -

Результирующая сила: сила Архимеда:

Подъемная сила или сила Архимеда прилагаемая в центре погруженной части тела, который называется центром водоимещения. Тело плавает, если вес его не превышает подъемную силу, которая действует со стороны жидкости.

Эпюры полного и избыточного гидростатических давлений.

b) На вертикальную стенку:

Рис. 13. Эпюры гидростатического давления на плоские вертикальные поверхности.

- полное гидростатичесое давление

- сила избыточного давления

- расстояние от свободной поверхности жидкости

до центра давления.

b) На наклонную стенку

- сила избыточного давления

Рис. 14. Эпюры гидростатического давления на наклоненные поверхности.

Дата добавления: 2014-10-15