
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Диссипативная функция Релея
|
|
|
|
Затухающее колебание
В реальных условиях на любую систему действует сопротивления различного характера (трение, сопротивление среды), поэтому гармонические колебания не встречаются и колебания любой системы будут являться затухающими. Поскольку сила сопротивления среды i –той точки системы противоположна и пропорциональна скорости, то сопротивление R будет равно:

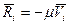
где  - коэффициент пропорциональности, характеризует свойства среды.
- коэффициент пропорциональности, характеризует свойства среды.
Происходит потеря кинетической энергии (рассеивание или диссипация), колебания для этой точки, тогда вводится диссипативная функция Релея
 ,
,
где b – обобщенный коэффициент диссипации.
Тогда обобщенная сила сопротивления равна:
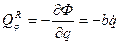
Таким образом, получим соответствующие уравнения:
 П=
П= 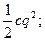

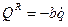
Тогда:
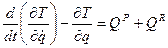
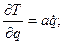

 (1)
(1)
Делим на а и получаем:

Введем обозначением:
 ;
;  ,
,
где n - коэффициент затухания.
Тогда для уравнения затухающих колебаний:
 (2)
(2)
Общий интеграл уравнения (2)
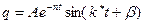 ,
,
где А - амплитудное значение затухающих колебаний;
 - начальная фаза колебания.
- начальная фаза колебания.
Частота колебаний равна
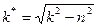
На графике колебаний:
 - декремент затухания, -nt - логарифм декремента затухания.
- декремент затухания, -nt - логарифм декремента затухания.
Период равен

 График затухающих колебаний имеет вид
График затухающих колебаний имеет вид
Если  , то нет полного цикла колебаний (лимитационное колебание)
, то нет полного цикла колебаний (лимитационное колебание)

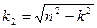
На этом основано действие автомобильных амортизаторов.
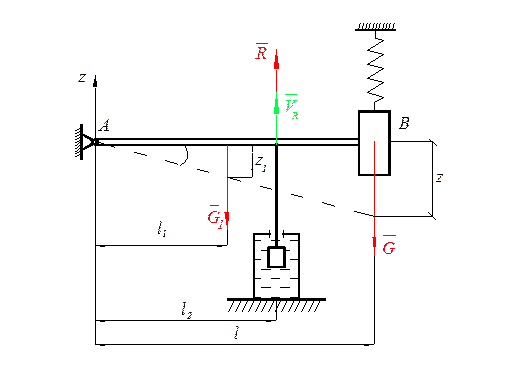 Пример: определить частоту, период колебаний передней подвески автомашины.
Пример: определить частоту, период колебаний передней подвески автомашины.
Выбираем обобщение координат
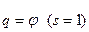
1) определим кинетическую энергию системы:

2) потенциальная энергия системы равна
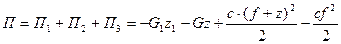
Т.к
 ;
; 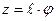
то
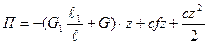 (1)
(1)
3) в положении равновесии 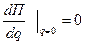
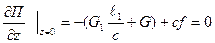 (2)
(2)
Подставляя полученное выражение (2) в (1), получим значение потенциальной энергии П в положении равновесия
П=  =
=  (3)
(3)

Сравнивая полученные выражения (1) и (3) с выражениями
 П=
П= 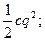
определяем значения коэффициентов а и с.
Частота таких колебаний находится по формуле
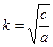
Но этого для решения задачи недостаточно, так как надо получить дифференциальное уравнение движения и определить, колебания являются гармоническими или затухающими.
Используя уравнения (1) и (3), получим уравнение типа
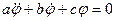
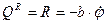 ;
; 



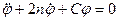

Колебания затухающие, тогда частота равна

Следовательно, определяем n и k
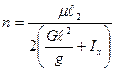 ;
; 
Вынужденные колебания
Предположим, что на систему в определенной точке действует периодически изменяющаяся сила с частотой ω:
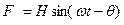 ,
,
где F – возмущающая сила;
ω – частота этой силы;
H – амплитудное значение;
θ – начальная фаза.
Тогда система будет совершать вынужденные колебания и поведение системы будет определяться в основном наличием сопротивления и частоты возмущающей силы 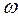 .
.
Тогда уравнение Лагранжа запишется:
 ,- Фр обобщеных сил (заданых сил)
,- Фр обобщеных сил (заданых сил)
где QR – обобщенная сила сил сопротивления;
QF – обобщенная сила сил возмущения.
Дифференциальное уравнение будет выглядеть:


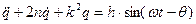 (1)
(1)
Уравнение (1) – дифференциальное уравнение вынужденных колебаний при наличии сил сопротивления.
Если сопротивление отсутствует, то n =0. Тогда система будет совершать гармонические колебания с частотой ω, но не с k.
Текущая амплитуда при наличии сил находится по формуле
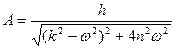
Если сопротивление отсутствует (т.е. n =0), то амплитуда равна
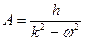
Если отсутствует сопротивление частоты собственных колебаний совпадают с частотой вынуждающих сил ( ), то наступает явление резонанса и амплитуда неограниченно возрастает (А → ∞). Конструкция разрушается.
), то наступает явление резонанса и амплитуда неограниченно возрастает (А → ∞). Конструкция разрушается.
Свойства вынужденных колебаний
1. Вынужденные колебания при линейном сопротивлении являются незатухающими с постоянной амплитудой.
2. Сопротивление не влияет на частоту вынужденных колебаний, которые совпадают с частотой возмущающей силы.
3. Вынужденные колебания при линейном сопротивлении не зависят от начальных условий.
4. Резонанс ( ) наступает при отсутствии (малом) сопротивлении и совпадении частот k и ω.
) наступает при отсутствии (малом) сопротивлении и совпадении частот k и ω.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 5501; Нарушение авторских прав?; Мы поможем в написании вашей работы!