Обобщенные координаты. Число степеней свободы

Независимые величины, заданием которых однозначно определяется местоположение любой точки системы, называются обобщенными координатами. Размерность их может быть различной.

Записывать эту величину будем q.

Число этих координат определяет число степеней свободы системы, в зависимости от чего в дальнейшем составляется определенное число дифференциальных уравнений, описывающих движение системы в обобщающих координатах.

Принцип виртуальных перемещений

Рассмотрим M_i -точку системы. Приложим к ней заданную силу и реакцию связи (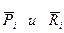), тогда точка находится в равновесии:

	δS

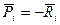
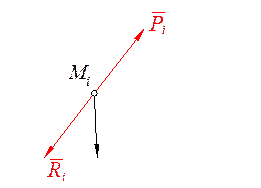
Дадим точке М_i возможное перемещение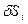допускаемое связью, и составим сумму элементарных работ 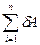на данном перемещении:

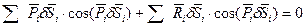
Т.к. связи идеальные, то второе слагаемое =0 и тогда:

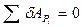
Таким образом, сумма элементарных возможных работ всех заданных сил на любом возможном перемещении допускаемые связями в любой момент времени равна нулю.

В векторной форме:,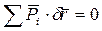

где 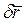-элементарное приращение радиус-вектора j – той точки.

В координатной форме:

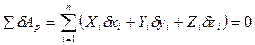
Дата добавления: 2014-10-15