Оценка чувствительности

Очевидно, что устойчивость является положительным свойством модели. Однако если изменение входных воздействий или параметров модели (в некотором заданном диапазоне) не отражается на значениях выходных параметров, то польза от такой модели невелика. В связи с этим возникает задача оценивания чувствительности модели к изменению параметров рабочей нагрузки и внутренних параметров самой системы.

Такую оценку проводят по каждому параметру модели в отдельности. Основана она на том, что обычно диапазон возможных изменений параметра известен. Данные, полученные при оценке чувствительности модели, могут быть использованы, в частности, при планировании экспериментов: большее внимание должно уделяться тем параметрам, по которым модель является более чувствительной.

1.4.Линейные пространства сигналов

Сформулируем математическую модель сигнала. Математическая модель сигнала x(t) устанавливает соответствие между любым моментом времени t 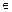T, где Т – ограниченный или бесконечный интервал времени (область определения сигнала), и величиной сигнала x 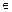X, где Х – множество возможных значений сигнала. Это соответствие может быть задано в форме скалярной функции x(t) или векторной функции (как, например, в многоканальных системах).

Сигнал, представленный в аналоговой форме, называется аналоговым сигналом, если множество Т возможных значений переменой t – континуум. Сигнал, представленный в виде последовательности чисел, называется дискретным сигналом, если подвергается временной дискретизации, то есть если множество Т возможных значений переменной t конечное или счетное. Сигнал представлен в цифровой форме и называется цифровым сигналом, если подвергается временной дискретизации и амплитудному квантованию, то есть если множество Т и Х возможных значений переменной t и функции x(t) – конечные илисчетные. Иными словами, цифровой сигнал – квантованный по амплитуде дискретный сигнал.

В теории систем связи и управления используются свойства и характеристики не только отдельных сигналов, а, главным образом, целых классов сигналов. Такой подход характерен для функционального анализа, при котором рассмотрение конкретных функций и связующих их соотношений заменено исследованием совокупностей функций, принадлежащих определенному классу пространств. Особый интерес представляют линейные пространства.

1.4.1.Определение и примеры линейных пространств

Определение. Непустое множество L элементов x, y, z,… называется линейным или векторным пространством, если оно удовлетворяет следующим условиям:

1. 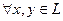однозначно определяет третий элемент 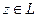называемой суммой и обозначаемый x + y. Сумма обладает свойствами:

1) 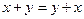– коммутативность;

2) 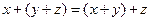– ассоциативность;

3) в L существует нулевой элемент 0, такой, что ;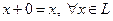

4) для 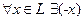, такой, то 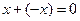(существует противоположный элемент).

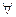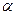2. Для числа и 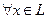определен элемент 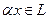(определено произведение числа на элемент), причем:

1) ;

2) ;

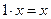3) ;

4) 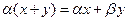(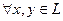и чисел ).

Если числа 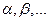– действительные, то L – действительное линейное пространство, если же комплексные, то L – комплексное линейное пространство.

Заметим, что всякое линейное комплексное пространство можно рассматривать как действительное, полагая мнимую часть равную нулю.

Примеры.

1. Совокупность действительных чисел, с обычными операциями сложения и умножения.

2. n -мерное векторное пространство (пространство дискретных сигналов), т.е. совокупность упорядоченных n чисел:

,

,

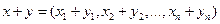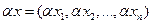
обозначается 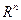в случае действительных чисел и 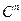– комплексных.

3. Сходящаяся последовательность 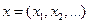с покоординатными операциями сложения и умножения.

1.4.2.Линейная зависимость

Элементы 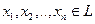называются линейно зависимыми, если существуют такие числа 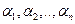, среди которых хотя бы одно не равное 0, что

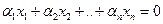(1.1)

В противном случае, они называются линейно независимыми. Другими словами, элементы 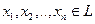называются линейно независимыми, если из тривиальной комбинации (1.1) следует, что

.

Бесконечная система элементов 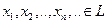называется линейно независимой, если ее любая подсистема линейно независима.

Если в L существует n линейно независимых элементов, а любые n+1 элементов этого пространства линейно зависимы, то говорят, что линейное пространство L имеет размерность n. При наличии бесконечного числа линейно независимых элементов говорят, что пространство L бесконечномерное. Базисом в n -мерном пространстве L называется любая система n линейно независимых элементов.

Пространства 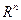и 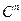как если проверить, имеют размерность n, оправдывая тем самым свое название.

Подпространства. Определение. Непустое множество элементов 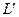линейного пространства L называются подпространством, если оно само образует линейное пространство по отношению к определенным в L операциям сложения и умножения на число.

Пример. Рассмотрим пространство непрерывных на интервале 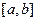функций 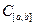и в нем совокупность всех многочленов 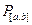. Ясно, что многочлены образуют в 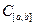подпространство.

1.4.3. Нормированное пространство

Определение. Линейное пространство L называется нормированным, если каждому элементу 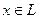ставится в соответствие неотрицательное число 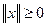(«длина» элемента 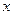), называемой нормой 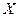, которое удовлетворяет условиям:

1) , тогда ;

2) 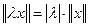, 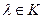– множество вещественных чисел;

3) 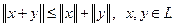(неравенство треугольника).

Нормированное пространство L можно превратить в метрическое, то-есть в линейное пространство, в котором введена метрика (расстояние между элементами 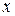и y пространства L)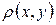. Метрика может быть введена произвольным образом, но при этом должны выполняться три аксиомы:

· ;

· ;

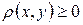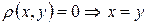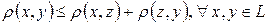· – неравенство треугольника.

Так, полагая 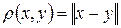, превращаем нормированное пространство L в метрическое. Можно и метрическое пространство превратить в нормированное, если метрика удовлетворяет условиям:

;

,

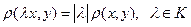положив .

Рассмотренное ранее пространство 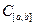и 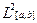становятся соответственно нормированными, если:

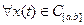· положим ;

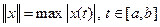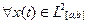· положим .

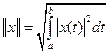Если положить 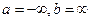, то квадрат этой нормы в теории сигналов носит название энергии сигнала

,

так как такая энергия выделяется на резисторе с сопротивлением 1 Ом при напряжении x (t) на его зажимах.

Пример. Имеется треугольный импульс длительности :

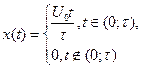
Вычислить энергию и норму сигнала.

Решение.

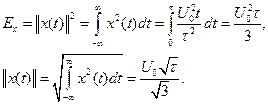
Определение. Полное нормированное пространство называется банаховым пространством или, короче, В-пространством (пространство Банаха).

1.4.4.Унитарное пространство

Определение. Нормированное пространство L называется унитарным, если в нем введено скалярное произведение, которое каждой паре элементов 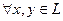ставит в соответствие число (комплексное, если L – множество комплексных чисел), обозначаемое (х, у), удовлетворяющее условиям:

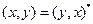· (* - знак комплексного сопряжения);

·

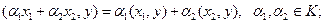
· если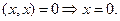

В унитарном пространстве норма вводится через скалярное произведение:

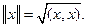
Для 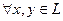(L – унитарное пространство) выполняется равенство Шварца (Коши-Буняковского):

.

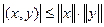Действительно, для любого вещественного квадратный многочлен

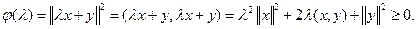
Дискриминант этого многочлена меньше или равен нулю, значит

.

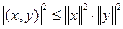Отсюда

.

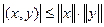Знак равенства выполняется, если элементы х и у линейно зависимы. Заметим, что при доказательстве неравенства Шварца, скалярное произведение считалось вещественным числом.

Определение. Два элемента (сигнала) называются ортогональными, если

.

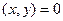Система элементов 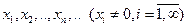унитарного пространства L называется ортогональной, если

.

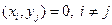Ее можно нормировать, положив

,

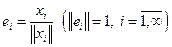тогда система 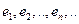называется ортонормированной.

Из ортонормированности системы следует ее линейная зависимость. Обратно, любую линейно независимую систему можно ортонормировать. Процесс ортонормированности следующий. Пусть система 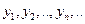– линейно независимая. Тогда система 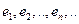– ортонормированная, где

.

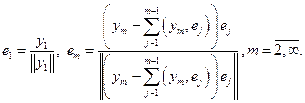Этот процесс ортогонализации носит название Грамма – Шмидта.

Определение. Система элементов 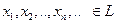будет называться полной, если она порождает это пространство, т.е. 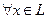можно представить в виде

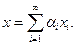
Введем в n -мерном унитарном пространстве L ортонормированный базис 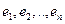. Тогда 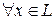можно записать

,

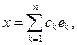где

.

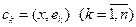Выясним, каким образом представление любого элемента через комбинацию базисных элементов может быть обобщено на случай унитарного пространства. Пусть

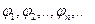
-ортонормированная система в унитарном пространстве L и 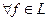. Сопоставим элементу 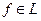последовательность чисел

,

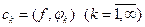которую будем называть координатами или обобщенными коэффициентами Фурье элемента 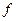по системе 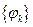. Ряд

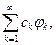
назовем обобщенным рядом Фурье элемента 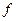ортогональной системы 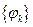. Возникает вопрос: сходится ряд Фурье? Чтобы ответить на этот вопрос, рассмотрим следующую задачу: при заданном n подберем координаты 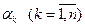так, чтобы расстояние между 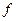и суммой 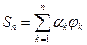было минимальным. С этой целью вычислим квадрат расстояния между 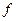и :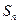

.

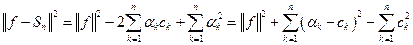Ясно, что минимум этого выражения достигается, если 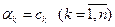. Причем, в этом случае

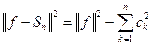. (1.2)

Итак, было доказано, что из всех сумм 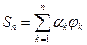при данном n наименее уклоняется от f частичная сумма ряда Фурье элемента f. Геометрически это можно пояснить следующим образом. Разность

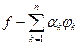
ортогональна всем линейным комбинациям вида

,

т.е. ортогональна подпространству, порожденному элементами в том и только в том случае, когда выполняется условие (1.2). Это обобщение геометрического результата: длина перпендикуляра, опущенного из данной точки на плоскость, меньше, чем длина любой наклонной, проведенной из этой же точки.

Так как 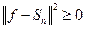, то

,

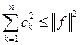а значит, в силу произвольности п ряд 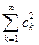сходится и .

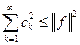Это, так называемое, неравенство Бесселя.

Определение. Ортонормированная система 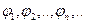называется замкнутой, если 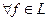справедливо равенство

.

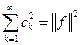В сепарабельном (пространство, в котором существует счетное всюду плотное множество) и унитарном пространстве L всякая полная ортонормированная система является замкнутой, и обратно. Или по-другому, чтобы в сепарабельном унитарном пространстве L ортонормированная система называлась полной, необходимо и достаточно, чтобы кроме нулевого элемента не существовало другого ортогонального элемента этой системы.

Определение. Полное унитарное пространство носит название пространства Гильберта (гильбертово пространство).

Примеры.

1. Система гармонических функций, записанных в комплексном

виде:

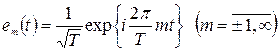
образует полную ортонормированную последовательность функций в .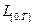

Пусть x (t) – финитный аналоговый сигнал (x (t) – функция, равная нулю вне интервала [0, T ]) и

x (t) =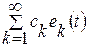, с_k =(x (t), e_k (t)).

Совокупность комплексных чисел с_k (k є Z) называют дискретным (линейчатым) спектром аналогового сигнала.

Тригонометрическая система

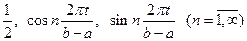
также образует полную ортогональную систему в пространстве .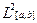

2. Функция вида

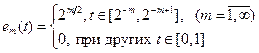
образует ортонормированную систему, состоящую из неотрицательных функций на отрезке [0, 1].

Дата добавления: 2014-10-15