Передаточные функции линейных звеньев

Рассмотрим динамическое звено, которое находится под воздействием полезного сигнала х(t) и возмущение f(t).

Рисунок 1 Динамическое звено

Тогда его динамика описывается линейным неоднородным дифференциальным уравнением вида:

(1)

преобразуем (1) по Лапласу при нулевых начальных условиях:

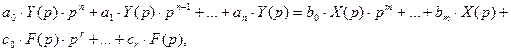(2)

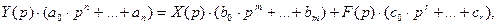(3)

N(p), M(p), R(p) -операторные полиномы с постоянными коэффициентами;

Y(p),X(p),F(p)- изображение функций y(t),x(t),f(t) соответственно.

Передаточной функцией звена, по какому либо внешнему воздействию называется отношение изображения по Лапласу выходной величины к изображению по Лапласу рассматриваемого воздействия, при этом все другие внешние воздействия полагаются равными нулю.

Из определения следует, что для любого звена с одной выходной величиной число передаточных функций равно числу внешних воздействий.

Тогда для рисунка1 передаточная функция звена по полезному сигналу, при F(p)=0:

= (4)

передаточная функция звена по возмущающему воздействию , при X(p)=0:

(5)

из уравнений (4) и (5) следует, что

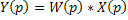
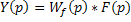(6)

Многочлен N(p),фигурирующий в знаменателе передаточных функций звена, называют характеристическим полином этого звена, а уравнение

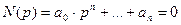
называется характеристическим уравнением звена. Оно представляет собой алгебраическое уравнение n-й степени и имеет n корней, среди которых могут быть как вещественные, так и комплексно-сопряженные.

Корни характеристического полинома называют полюсами передаточной функции, корни многочлена стоящего в числителе передаточной функции – нулями этой передаточной функции

Если известны передаточные функции для звена на рисунке 1, то изображение выходной величины, согласно принципу суперпозиции:

или (7)

Соотношение (7) удобно представить в виде структурной схемы звена (рисунок 2).

Рисунок 2 Структурная схема звена

ПРИМЕР 1: Дифференциальное уравнение звена имеет вид:

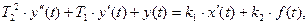(8)

Найти передаточные функции звена. Получить структурную схему.

РЕШЕНИЕ: По дифференциальному уравнению (8) составим операторное уравнение, используя преобразование по Лапласу и его свойства.

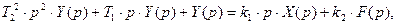
Полагая F(p)=0, найдем передаточную функцию звена по полезному сигналу.

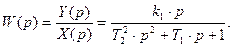
Полагая X(p)=0, найдем передаточную функцию звена по возмущающему воздействию:

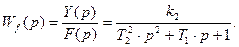
Структурная схема звена представлена на рисунке 2.

ПРИМЕР 2. Структурная схема звена имеет вид (рисунок. 2). Передаточные функции определяются по выражениям:

Найти дифференциальное уравнение звена.

РЕШЕНИЕ:

Операторное уравнение звена:

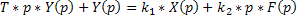
Применяя обратное преобразование Лапласа и его свойства, получим дифференциальное уравнение:

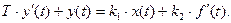
Дата добавления: 2014-10-15