
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Криволинейное движение (равномерное движение по окружности)
|
|
|
|
   a)
a) 
 б)
б) 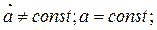
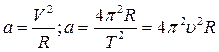 в)
в)  г)
г)  д)
д) 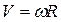
|  –линейная скорость, в каждой точке направлена по касательной к окружности –линейная скорость, в каждой точке направлена по касательной к окружности
 –центростремительное ускорение, в каждой точке направлено по радиусу к центру окружности –центростремительное ускорение, в каждой точке направлено по радиусу к центру окружности
 –радиус окружности –радиус окружности
 –период обращения по окружности –период обращения по окружности
 –частота обращения –частота обращения
 –угловая скорость –угловая скорость
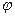 - угол поворота точки по окружности за промежуток времени - угол поворота точки по окружности за промежуток времени 
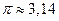
|
4. Закон сложения скоростей в классической механике.

С.О. – система отсчёта;
 – скорость движения тела относительно С.О. «К1»;
– скорость движения тела относительно С.О. «К1»;
 – скорость движения тела относительно С.О. «К2»;
– скорость движения тела относительно С.О. «К2»;
 – скорость движения С.О. «К1» относительно
– скорость движения С.О. «К1» относительно
Примеры решения задач
1. Из начальной точки с координатами  тело прошло некоторый путь, так что проекция его перемещения на ось
тело прошло некоторый путь, так что проекция его перемещения на ось  оказалась равной 4м, а на ось
оказалась равной 4м, а на ось  – 3м. Найдите координаты конечного положения точки. Начертите вектор перемещения. Чему равен его модуль?
– 3м. Найдите координаты конечного положения точки. Начертите вектор перемещения. Чему равен его модуль?
Дано: Решение:

 1. Зная, что
1. Зная, что  и
и  , находим:
, находим:
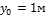

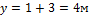
 2. Построим вектор перемещения
2. Построим вектор перемещения








 4 2
4 2
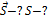
3



1 


 1
1
 |
0 1 2 3 4 5 6 7  (м)
(м)
Начальная точка «1» с координатами 3м и 1м, конечная точка перемещения «2» с координатами 7м и 4м. Вектор, проведённый из начальной точки в конечную точку, есть вектор перемещения 
3. Модуль вектора перемещения  находим из прямоугольного треугольника по теореме Пифагора:
находим из прямоугольного треугольника по теореме Пифагора:
 =
= 
2. Вертолёт, пролетев по прямой 20 км, повернул под углом 90˚ и пролетел ещё 15 км. Найти путь и перемещение вертолёта.
 Дано: Решение:
Дано: Решение:
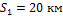 1. Пройденный путь
1. Пройденный путь 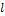 – длина траектории,
– длина траектории, 


 2. Результирующее перемещение
2. Результирующее перемещение  найдём,
найдём,
 складывая векторы по правилу треугольника:
складывая векторы по правилу треугольника:
 3. Модуль вектора перемещения найдём
3. Модуль вектора перемещения найдём




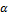 из прямоугольного треугольника
из прямоугольного треугольника


по теореме Пифагора:  ;
;

4. Найдём, под каким углом к первоначальному перемещению совершено результирующее перемещение. Из треугольника видно, что 
Ответ: вертолёт переместился на 25 км под углом 37˚ к первоначальному направлению, пройдя путь 35 км.
3. Точка движется равномерно и прямолинейно противоположно положительному направлению оси Ox. В начальный момент времени точка имела координату x0 = 12м. Найдите координату точки спустя 6 с от начала отсчёта времени, если модуль её скорости равен v = 3 м/с. Чему равен путь, пройденный точкой за это время.
Дано:
x0 = 12 м
V = 3 м/с
t= 6c


| Решение:
т.к.  , то , то  координату найдём по уравнению
координату найдём по уравнению
 по уравнению
по уравнению  найдём проекцию перемещения найдём проекцию перемещения  Пройденный путь S = 18 м
Ответ: x = –6 м; S = 18 м.
Пройденный путь S = 18 м
Ответ: x = –6 м; S = 18 м.
|
4. Движения двух велосипедистов заданы уравнениями:  ,
,  . Построить графики зависимости x(t). Найти время и место встречи.
. Построить графики зависимости x(t). Найти время и место встречи.
Дано:


| Решение:
1.Определяем пару точек для построения графиков обоих тел.
I велосипедист: 
II велосипедист:
2. По точкам строим графики:
Место встречи – это точка, в которой координаты тел одинаковы. Находим точку пересечения графиков. Опуская перпендикуляр из этой точки на ось X, находим место встречи x = 50 м. Опуская из этой точки перпендикуляр на ось t, находим время встречи t = 10 с. | ||||||||||||
 (графики) (графики)

|
5. По заданным графикам найти начальные координаты тел и проекции скорости их движения. Написать уравнения движения тел x = x(t). Из графиков и уравнений найти время и место встречи тел, движения которых описываются графиками II и III.

Решение:
1. В общем виде уравнение движения:  .
.
I тело:  м. По графику видно, что его координата со временем не изменяется,тело не движется.
м. По графику видно, что его координата со временем не изменяется,тело не движется.
 ; уравнение движения x = 5.
; уравнение движения x = 5.
II тело: По графику определяем
 м
м
 с;
с; 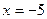 м
м
 с;
с;  м/с
м/с
уравнение движения: 
III тело: По графику находим:
 м
м
 с;
с;  ;
;
 с
с
 м/с
м/с
уравнение движения: 
2. Определяем точку пересечения графиков II и III тел.
Координаты этой точки x = –5 м место встречи, t = 10 c время встречи.
3. Используя уравнения

 , находим время встречи t:
, находим время встречи t:
т.к.  во время встречи, то
во время встречи, то 
 с.
с.
Подставляя время в одно из уравнений, находим место встречи:
 м или
м или  м.
м.
6. Тело движется вдоль координатной оси. В начальный момент времени направление скорости тела совпадало с направлением оси. Модуль скорости тела  м/с. Найдите скорость тела через 5 с и 7 с от начала отсчёта времени, если ускорение направлено противоположно начальной скорости и его модуль
м/с. Найдите скорость тела через 5 с и 7 с от начала отсчёта времени, если ускорение направлено противоположно начальной скорости и его модуль  м/с2.
м/с2.
Дано:
 м/с м/с
 с с
 с с
 м/с2 м/с2
| Решение:
Т.к.  , то , то  . .
 , ,  ;
Используем уравнение скорости для равноускоренного прямолинейного движения ;
Используем уравнение скорости для равноускоренного прямолинейного движения

 м/с м/с
 м/с
Ответ: через 5 с скорость уменьшится до 0, тело остановится и далее начнёт двигаться в противоположную сторону, через 7 с скорость станет равной 8 м/с и направлена будет против оси м/с
Ответ: через 5 с скорость уменьшится до 0, тело остановится и далее начнёт двигаться в противоположную сторону, через 7 с скорость станет равной 8 м/с и направлена будет против оси  . .
|

|
7. Два мотоциклиста выезжают одновременно из двух пунктов навстречу друг другу. Один из них спускается равноускоренно с горы, имея начальную скорость 36 км/ч и ускорение 2 м/с2. Другой равнозамедленно поднимается в гору с начальной скоростью 72 км/ч и с тем же по модулю ускорением. Первоначальное расстояние между мотоциклистами равно 300м. Через сколько времени они встретятся?
Дано:
1 мотоциклист:
 км/ч = 10 м/с
2 мотоциклист: км/ч = 10 м/с
2 мотоциклист:
 км/ч = 20 м/с км/ч = 20 м/с
 м/с м/с
 м м
| Решение:   0 0
    →
→
 α2 α2
 
 ◦
300 ◦
300
 Выберем направление оси OX с горы вниз, тогда
Выберем направление оси OX с горы вниз, тогда
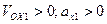 ; ;  < 0; < 0; >0
Если в начальный момент времени 1го мотоциклиста поместить в начало координат, то >0
Если в начальный момент времени 1го мотоциклиста поместить в начало координат, то  , тогда второй мотоциклист, находясь на расстоянии 300 м от первого, будет иметь начальную координату , тогда второй мотоциклист, находясь на расстоянии 300 м от первого, будет иметь начальную координату  м.
Используя уравнение координаты для равноускоренного движения, запишем это уравнение для обоих тел: м.
Используя уравнение координаты для равноускоренного движения, запишем это уравнение для обоих тел:
 

 В момент встречи
В момент встречи  , т.е. , т.е.  Решая уравнение, находим t – момент встречи
Решая уравнение, находим t – момент встречи
 с
Ответ: мотоциклисты встретятся через 10 с. с
Ответ: мотоциклисты встретятся через 10 с.
|
 (время встречи) (время встречи)
|
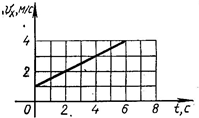
8. Пользуясь графиком проекции скорости найти начальную скорость, скорости в начале четвёртой и в конце шестой секунд. Вычислить ускорение и написать уравнение  .
.
Решение:
1.  м/с
м/с
2. Скорость в начале четвёртой секунды – это скорость за 3 с.
 с;
с;  м/с
м/с
3.  с;
с;  м/с
м/с
4. 
 м/с;
м/с;  м/с;
м/с;  с.
с.
Скорость от 1 м/с до 4 м/с изменится за 6 с.
 м/с2
м/с2
5. Уравнение скорости для равноускоренного движения в общем виде:  , в нашем случае:
, в нашем случае:  .
.
9. Уравнение движения материальной точки имеет вид  . Написать формулу зависимости
. Написать формулу зависимости  и построить график. Показать на графике штриховкой площадь, численно равную пути, пройденному точкой за 4 с, и вычислить этот путь.
и построить график. Показать на графике штриховкой площадь, численно равную пути, пройденному точкой за 4 с, и вычислить этот путь.
Дано:

| Решение:
1. Сравнивая уравнение данного движения с уравнением движения равноускоренного в общем виде  и и  , устанавливаем, что для данного движения , устанавливаем, что для данного движения  .
Если представить .
Если представить  , то ясно, что , то ясно, что  м/с2.
Уравнение скорости для равноускоренного движения в общем виде м/с2.
Уравнение скорости для равноускоренного движения в общем виде , для нашего движения , для нашего движения  2. Для построения графика найдём две точки:
Vx (м/с)
2. Для построения графика найдём две точки:
Vx (м/с)
1 2 3 4 5 t(c) 3. Пройденный путь и перемещение в данном прямолинейном движении совпадают. Используя уравнение перемещения для равноускоренного движения находим пройденный путь Если представить | ||||||
1.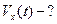 (уравнение)
2. (уравнение)
2. 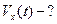 (график)
3. (график)
3.  за за  с (показать на графике) с (показать на графике)
| |||||||
10. По двум параллельным железнодорожным путям навстречу друг другу равномерно движутся два поезда со скоростями 72 км/ч и 102 км/ч. Длина первого поезда 900 м, второго – 140 м. В течение какого времени один поезд проходит мимо другого?
Дано:
1 поезд – тело
2 поезд СО «К1»
Земля – СО «К2»
 км/ч = 20 м/с км/ч = 20 м/с
 км/ч км/ч  м/с м/с
 м м
 м м
| Решение:
 скорость тела относительно СО «К2», т.е. первого поезда относительно Земли; скорость тела относительно СО «К2», т.е. первого поезда относительно Земли;
 скорость СО «К1» относительно СО «К2», т.е. 2-го поезда относительно Земли
1. Найдём скорость V1, с которой движется первый поезд относительно второго, т.е. скорость тела относительно СО «К1», используя классический закон сложения скоростей скорость СО «К1» относительно СО «К2», т.е. 2-го поезда относительно Земли
1. Найдём скорость V1, с которой движется первый поезд относительно второго, т.е. скорость тела относительно СО «К1», используя классический закон сложения скоростей
 в проекциях на ось OX
в проекциях на ось OX



 В итоге уравнение принимает вид
В итоге уравнение принимает вид
 м/с
2. С такой скоростью один поезд проходит мимо другого путь l1 + l2 =
=900+140=1040 м м/с
2. С такой скоростью один поезд проходит мимо другого путь l1 + l2 =
=900+140=1040 м

|

| |
11. Какую скорость относительно воды должен сообщить мотор катеру, чтобы при скорости течения реки, равной 2м/с, катер двигался перпендикулярно к берегу со скоростью 3,5 м/с относительно берега?
| Дано: катер – тело река – СО «К1» берег – СО «К2» V = 2 м/с (скорость реки относительно берега) V2 = 3,5 м/с (скорость катера относительно берега) | Решение:
Согласно классическому закону сложения скоростей.
 При сложении векторов по правилу треугольника получаем следующий треугольник скоростей:
При сложении векторов по правилу треугольника получаем следующий треугольник скоростей:
 
  
    β α β α 
 
т.к. полученный треугольник прямоугольный, используем теорему Пифагора (модуль скорости) Чтобы найти направление скорости
Ответ: катер относительно воды должен двигаться со скоростью 4 м/с под углом 60° к берегу против течения реки. | |||
 (скорость катера относительно реки) (скорость катера относительно реки)
| ||||
12. Линейная скорость периферийных точек шлифовального камня не должна превышать 95 м/с. Определите наибольшее допустимое число оборотов в минуту для диска диаметром 30 см.
| Дано: t = 1 мин = 60 с V = 95 м/с D = 30 см = 0,3 м | Решение:
1. 2.
2.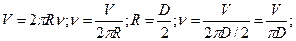
 Ответ: 6051 оборотов в минуту
Ответ: 6051 оборотов в минуту
|

| |
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1836; Нарушение авторских прав?; Мы поможем в написании вашей работы!


 t
t
 0
0

 4
4
 3
3
 2
2
 1
1 0
0 ,
, м.
м. , то видим, что S – площадь треугольника под графиком.
, то видим, что S – площадь треугольника под графиком.
 , тогда
, тогда  м/с
м/с , определим сначала угол
, определим сначала угол  , а затем
, а затем .
. .
.