Число степей свободы. Универсальная структурная формула

Классификация механизмов и виды звеньев

Классификация кинематических пар

Совокупность поверхностей, линий и отдельных точек звена, по которым оно может соприкасаться с другим звеном, образуя кинематическую пару, называется элементом кинематической пары.

Кинематические пары делятся на низшие и высшие.

Таблица 1

Wr	Sr	Название пары	Рисунок	Условное обозначение
		Поступательная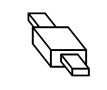
		Вращательная
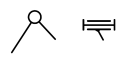
		Винтовая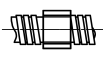
		Цилиндрическая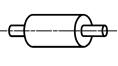
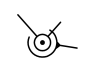
		Сферическая с пальцем
		Сферическая
		Плоскостная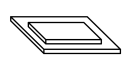
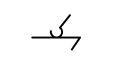
		Цилиндр-плоскость
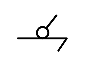
		Шар-плоскость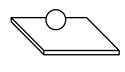

Низшей называется кинематическая пара, в которой относительное движение двух звеньев может быть получено постоянным соприкосновением ее элементов по поверхности.

Высшей называется кинематическая пара, в которой относительное движение двух звеньев может быть получено соприкосновением ее элементов только линиями или точками.

Введем обозначения:

Н – число степеней свободы в относительном движении двух звеньев, образующих кинематическую пару;

S – число уравнений геометрических связей, налагаемых на относительное движение указанных звеньев.

Всегда выполняется равенство: Н+S=6.

Число S уравнений связей принимается за номер класса кинематической пары, а в зависимости от числа пары подразделяются на одно-, двух-, трех-, четырех- и пятиподвижные.

Так, если Н = 1 и соответственно S = 5, то данная пара является одноподвижной и относится к пятому классу.

В зависимости от характера относительного движения двух звеньев, кинематические пары могут быть различного вида.В табл.1 приведены девять видов кинематических пар вместе с соответствующими значениями Н и S, а также условными графическими обозначениями пар. Пары вида «цилиндр – плоскость» и «шар – плоскость» относятся к высшим, а семь предыдущих пар в табл.1 – к низшим. Для шести первых видов пар (см. табл.1) введем буквенные обозначения: П (поступательная), В (вращательная), Ви (винтовая), Ц (цилиндрическая), С_п (сферическая с пальцем) и С (сферическая).

Механизмы делятся на плоские и пространственные.

Механизм называется плоским, когда все точки его подвижных звеньев движутся во взаимно параллельных плоскостях. В других случаях механизм называют пространственным.

Среди всего многообразия механизмов выделяют следующие группы механизмов: рычажные, кулачковые, зубчатые, фрикционные, с гибкими связями(ременная передача, цепная передача) и др.

Звенья рычажных механизмов образуют друг с другом пары вида П, В, Ви, Ц, С_п или С, причем в плоских рычажных механизмах встречаются только одноподвижные пары - П и В.

За звеньями механизмов в зависимости от характера их движения закрепились определенные названия.

Кривошип – звено, которое образует вращательную пару со стойкой и может совершать полный оборот вокруг оси этой пары.

Коромысло – звено, которое образует вращательную пару со стойкой и может совершать только неполный оборот вокруг оси этой пары. С подвижным звеном кривошип и коромысло образуют, как правило, вращательную пару.

Ползун – звено, образующее поступательную пару со стойкой и движущееся прямолинейно - поступательно.

Шатун – звено, образующее кинематические пары только с подвижными звеньями.

Кулиса – звено, вращающееся вокруг неподвижной оси и образующее с другим подвижным звеном поступательную пару.

Кулачок – звено, которому принадлежит элемент высшей пары, выполненный в виде поверхности или кривой переменной кривизны.

Зубчатое звено – звено, имеющее выступы (зубья) для передачи движения посредством взаимодействия с выступами другого звена (тоже зубчатого). Вращающееся зубчатое звено называется зубчатым колесом.

В дальнейшем будем рассматривать плоские рычажные механизмы. Некоторые схемы плоских рычажных механизмов показаны на рис.1, рис.2 и рис.13.

В шестизвенном механизме первого типа (см. рис.1) входное звено 1 является кривошипом, звенья 3 и 5 – коромыслами, а звенья 2 и 4 – шатунами. В четырехзвенном механизме второго типа (рис.2) звено 1 – кулиса, 2 – шатун, 3 – коромысло. В четырехзвенном механизме первого типа (рис.13) входное звено 1 – ползун, звено 2 – шатун, а звено 3 — коромысло.

Независимые между собой параметры (линейные или угловые), однозначно определяющие положение всех звеньев механизма относительно стойки, называются обобщенными координатами механизма.

Число обобщенных координат называется числом степеней свободы или подвижностью механизма.

В качестве обобщенных координат механизма обычно принимают относительные перемещения звеньев, образующих входные кинематические пары. Например, в механизмах, показанных на рис.1,2 в качестве обобщенной координаты принимают: угол φ (рис.1) или линейный параметр S (рис.2 и 13).

Для плоских рычажных механизмов без избыточных связей подвижность W определяется при помощи универсальной структурной формулы.

W = 3(n –1) – 2p, (1)

где n – число звеньев механизма (включая стойку); р – число кинематических пар.

Для механизма, показанного на рис.13, имеем: n= 4; W = 1; для механизма на рис.1 n = 6, р = 7, W = 1.

Формула (1) не выполняется для механизмов с избыточными связями.

Избыточными связями в механизме называются связи, которые повторяют (дублируют) ограничения, наложенные другими связями.

Число qизбыточных связей и подвижность W механизма связаны соотношением:

W = 3(n – 1) – 2p + q (2)

Избыточные связи могут существовать только при особых соотношениях между постоянными параметрами кинематической схемы механизма. Так, в механизме двойного параллелограмма (рис.14) выполняются соотношения: АВ=CD,BE=CF, AD=BC=EF. В этом механизме n = 5, р = 6, q = 1, W = 1.

Дата добавления: 2014-10-15