Способы образования индексов и связь между ними

Построение общих индексов может осуществляться в форме агрегатных или средних индексов.

Основной формой общих индексов являются агрегатные индексы, в числителе и знаменателе которых содержатся соединенные наборы (агрегаты) элементов изучаемых совокупностей. Агрегатные индексы необходимы для перехода от натуральных измерителей разнородных единиц статистической совокупности к однородным показателям с тем, чтобы получить сопоставимость разнородных единиц в сложных статистических совокупностях. При этом в числителе и знаменателе агрегатного индекса изменяется лишь значение индексируемой величины, а их соизмерители (множители) являются постоянными и фиксируются на одном уровне. Таким образом, на величине индекса сказывается лишь влияние фактора, который определяет изменение индексируемой величины.

Например, в агрегатной форме общий индекс цен с весами текущего периода (индекс Пааше)

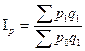
в качестве индексируемых величин содержит цены отчётного () и базисного () периодов, а в качестве соизмерителей (весов) используются данные о количестве разнородных товаров () в текущем периоде. В числителе индекса при суммировании по всей совокупности товаров образуется сумма стоимости товаров в текущем периоде по ценам того же периода (), а в знаменателе – значение стоимости товаров в текущем периоде по ценам базисного периода (). В данном случае индекс Пааше характеризует динамику (изменение) общего уровня цен по рассматриваемому ассортименту товаров вследствие влияния на изменение цен фактора времени. Разность числителя и знаменателя индекса определяет абсолютный прирост стоимостного объёма товаров в текущем периоде, за счёт фактора изменения цен в текущем периоде по сравнению с базисным периодом:

При другом способе определения агрегатного индекса цен в качестве соизмерителя индексируемых величин и могут использоваться данные о количестве товаров в базисном периоде . Агрегатная форма такого общего индекса цен с весами базисного периода (индекс Ласпейреса) имеет вид:

Разность числителя и знаменателя индекса Ласпейреса определяет абсолютный прирост в стоимостном объёме товаров базисного периода, если бы они продавались по ценам отчётного периода:

.

Индексы Пааше и Ласпейреса в общем случае различаются, поскольку характеризуют различные эффекты от изменения цен. Применение индексов Пааше и Ласпейреса зависит от цели исследования. Если исследование проводится для определения экономического эффекта отчётного периода от изменения цен в отчётном периоде по сравнению с базисным, то применяют индекс Пааше. Если же целью анализа является характеристика стоимостного объёма товаров такого же количества, что в базисном периоде, но по ценам текущего периода, то применяют индекс Ласпейреса.

Иногда при образовании общего индекса цен вместо фактического количества товаров (или ) в качестве соизмерителей индексируемых величин (и ) применяются средние величины количества товаров . При таком способе образования формула общего индекса имеет вид

где - среднее значение количества товаров (физический объём), рассчитываемое различными методами в зависимости от того, какие данные по количеству товаров имеются в наличии и какие цели анализа преследуются.

В экономической статистике также широко применяются агрегатные индексы физического объёма товаров.

Если в качестве индексируемых величин выступают количества товаров (и ), а соизмерителем является цена базисного периода то общий индекс физического объёма имеет вид

В случае, если в качестве соизмерителей привлекаются цены отчётного периода то общий индекс физического объёма имеет вид

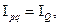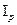Взаимосвязь общих индексов стоимостного объёма цен и физического объёма 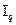всегда обусловлена фундаментальной связью стоимости, цены и количества () и может быть представлена выражением

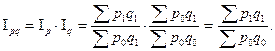
Важной особенностью общих агрегатных и индивидуальных индексов является то, что они определяют не только относительное значение изменения изучаемого явления, но с их помощью можно найти абсолютные значения изменений. Если из числителя каждого индекса вычесть его знаменатель, то можно получить абсолютные приросты: общий прирост сопоставляемой величины и в том числе приросты за счёт отдельных факторов. Например, общий прирост стоимости товаров в отчётном периоде по сравнению с базисным равен

в том числе прирост стоимости за счёт изменения цен равен и за счёт изменения физического объёма товаров равен

Иногда в статистике применяются общие индексы цен и физического объёма, предложенные американским экономистом И.Фишером. Индекс цен Фишера представляет собой среднюю геометрическую двух агрегатных индексов цен Пааше и Ласпейреса:

Соответствующая формула для определения индекса физического объёма имеет вид:

Индекс цен Фишера в силу относительной сложности расчёта и трудности экономической интерпретации на практике используется довольно редко. Чаще всего он применяется для исчисления индексов цен за длительный период времени для сглаживания тенденций в структуре и составе объёма продукции, в которых происходят значительные изменения.

Рассмотренная методика определения общих индексов цен в агрегатной форме аналогично применяется при построении индексов других качественных показателей: себестоимости производительности труда и др. Примеры взаимосвязей общих индексов:

где - общие индексы объёма продукции и объёма себестоимости продукции, соответственно; - общие индексы производительности труда и себестоимости единицы продукции, соответственно; - общие индексы численности работников и физического объёма продукции, соответственно.

Одной из форм выражения общих индексов являются средние индексы: средний арифметический взвешенный индекс и средний гармонический взвешенный индекс.

Средний арифметический индекс строится таким образом, что он тождественен агрегатным индексам экстенсивных объёмных показателей. Так, например, агрегатный индекс физического объёма преобразуется в средний арифметический взвешенный индекс физического объёма (с учётом, что

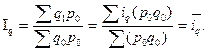
Средний гармонический индекс является преобразованной формой агрегатных индексов качественных интенсивных показателей (цен, себестоимости единицы продукции, производительности труда работника и др.) Например, агрегатный индекс цен преобразуется в формулу гармонического взвешенного индекса цен (с учётом, что ):

Таким образом, средние индексы рассчитываются как средние величины индивидуальных индексов, причём средний арифметический индекс (например 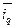) исчисляется с весами по стоимостному объёму базисного периода (), а средний гармонический индекс (например ) исчисляется с весами по стоимостному объёму отчётного периода ().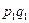

Выбор формы индекса в виде агрегатного или среднего зависит от характера исходных данных. Условием применения в экономической статистике агрегатных индексов является наличие данных о натуральных измерителях (соизмерителей) и их качественном содержании (например, количество и цена каждого вида товара). Если известны изменения индексируемого показателя и его веса по отдельным единицам совокупности, то пользуются формой средних индексов.

При изучении динамики явлений за три и большее количество периодов индексы могут быть исчислены двумя путями:

а) путём сопоставления показателей всех периодов поочерёдно с показателем одного периода, принятого за постоянную базу. Такие индексы с постоянным основанием называют базисными;

б) путём сопоставления показателей каждого периода с величиной показателя непосредственно предшествующего периода. Такие индексы называют цепными.

Базисные и цепные индексы связаны между собой следующими правилами:

а) перемножив все цепные, получим последний базисный;

б) разделив каждый последующий базисный на предыдущий базисный, получим цепной индекс.

Дата добавления: 2014-10-15