Решение. 1.Для расчета параметров уравнения линейной регрессии строим расчетную таблицу D.2

1. Для расчета параметров уравнения линейной регрессии строим расчетную таблицу D.2.

Таблица D.2

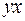
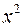
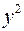
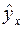
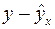
							-16	12,0
							-4	2,7
							-23	17,2
								2,6
								1,9
								10,8
								0,0
								0,0
								5,3
								3,1
								7,5
							-10	5,8
Итого								68,9
Среднее значение	85,6	155,8	13484,0	7492,3	24531,4	–	–	5,7
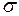
	12,84	16,05	–	–	–	–	–	–
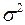
	164,94	257,76	–	–	–	–	–	–

;

.

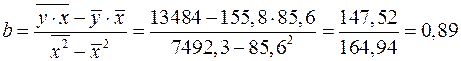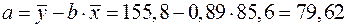Получено уравнение регрессии: .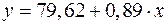

С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,89 руб.

2. Тесноту линейной связи оценит коэффициент корреляции:

; .

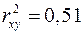Это означает, что 51% вариации заработной платы () объясняется вариацией фактора – среднедушевого прожиточного минимума.

Качество модели определяет средняя ошибка аппроксимации:

.

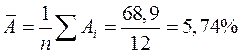Качество построенной модели оценивается как хорошее, так как 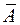не превышает 8-10%.

3. Оценку значимости уравнения регрессии в целом проведем с помощью 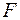-критерия Фишера. Фактическое значение 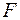-критерия:

.

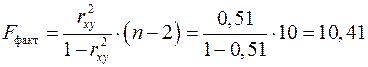Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы 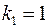и 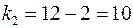составляет 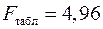. Так как 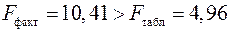, то уравнение регрессии признается статистически значимым.

Оценку статистической значимости параметров регрессии проведем с помощью -статистики Стьюдента и путем расчета доверительного интервала каждого из показателей.

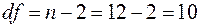Табличное значение -критерия для числа степеней свободы и 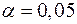составит .

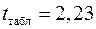Определим случайные ошибки , , :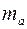

;

;

.

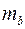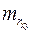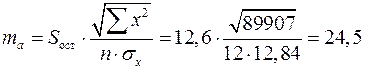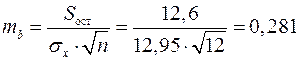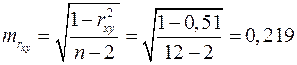Тогда

;

;

.

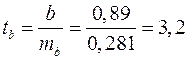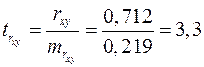Фактические значения -статистики превосходят табличное значение:

; ; ,

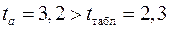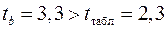поэтому параметры 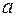, 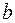и 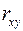не случайно отличаются от нуля, а статистически значимы.

Рассчитаем доверительные интервалы для параметров регресси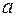и и 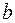. Для этого определим предельную ошибку для каждого показателя:

;

.

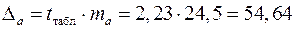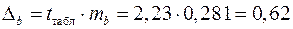Доверительные интервалы

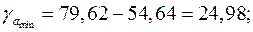
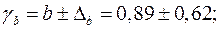
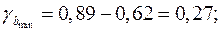
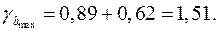
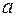Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры и 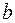, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.

4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: 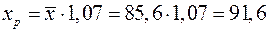руб., тогда прогнозное значение заработной платы составит: 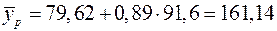руб.

5. Ошибка прогноза составит:

.

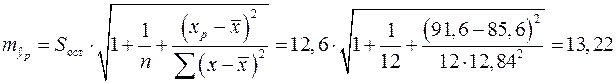Предельная ошибка прогноза, которая в 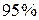случаев не будет превышена, составит:

.

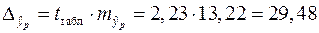Доверительный интервал прогноза:

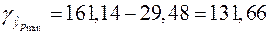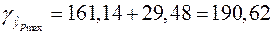руб.;

руб.

Выполненный прогноз среднемесячной заработной платы является надежным (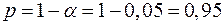) и находится в пределах от 131,66 руб. до 190,62 руб.

6. В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую (рис. D.1):

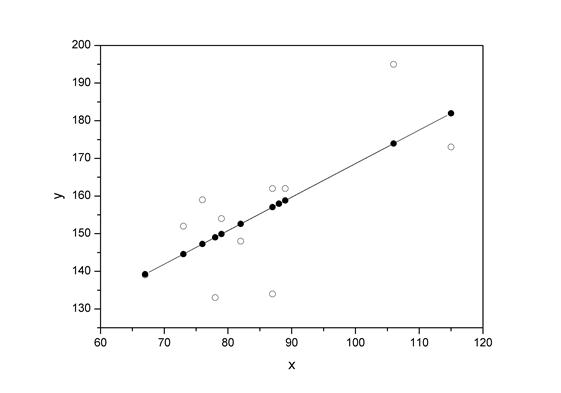
Рис. D.1.

Варианты индивидуальных заданий

Задача 1. По территориям региона приводятся данные за 199X г. (см. таблицу своего варианта).

Требуется:

1. Построить линейное уравнение парной регрессии от .

2. Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции с помощью 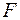-критерия Фишера и -критерия Стьюдента.

4. Выполнить прогноз заработной платы при прогнозном значении среднедушевого прожиточного минимума , составляющем 107% от среднего уровня.

5. Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал.

6. На одном графике построить исходные данные и теоретическую прямую.

Вариант 1

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	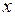Среднедневная заработная плата, руб.,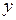

Вариант 2

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	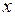Среднедневная заработная плата, руб.,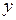

Вариант 3

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	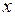Среднедневная заработная плата, руб.,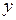

Вариант 4

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	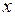Среднедневная заработная плата, руб.,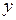

Вариант 5

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	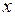Среднедневная заработная плата, руб.,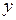

Вариант 6

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	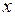Среднедневная заработная плата, руб.,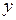

Вариант 7

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	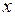Среднедневная заработная плата, руб.,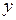

Вариант 8

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	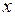Среднедневная заработная плата, руб.,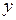

Вариант 9

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	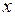Среднедневная заработная плата, руб.,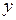

Вариант 10

Номер региона	Среднедушевой прожиточный минимум в день одного трудоспособного, руб.,	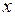Среднедневная заработная плата, руб.,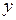

Дата добавления: 2014-10-15