Решение. Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу: №

Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу:

№
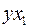
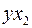
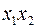
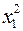
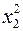
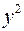
	7,0	3,9	10,0	27,3	70,0	39,0	15,21	100,0	49,0
	7,0	3,9	14,0	27,3	98,0	54,6	15,21	196,0	49,0
	7,0	3,7	15,0	25,9	105,0	55,5	13,69	225,0	49,0
	7,0	4,0	16,0	28,0	112,0	64,0	16,0	256,0	49,0
	7,0	3,8	17,0	26,6	119,0	64,6	14,44	289,0	49,0
	7,0	4,8	19,0	33,6	133,0	91,2	23,04	361,0	49,0
	8,0	5,4	19,0	43,2	152,0	102,6	29,16	361,0	64,0
	8,0	4,4	20,0	35,2	160,0	88,0	19,36	400,0	64,0
	8,0	5,3	20,0	42,4	160,0	106,0	28,09	400,0	64,0
	10,0	6,8	20,0	68,0	200,0	136,0	46,24	400,0	100,0
	9,0	6,0	21,0	54,0	189,0	126,0	36,0	441,0	81,0
	11,0	6,4	22,0	70,4	242,0	140,8	40,96	484,0	121,0
	9,0	6,8	22,0	61,2	198,0	149,6	46,24	484,0	81,0
	11,0	7,2	25,0	79,2	275,0	180,0	51,84	625,0	121,0
	12,0	8,0	28,0	96,0	336,0	224,0	64,0	784,0	144,0
	12,0	8,2	29,0	98,4	348,0	237,8	67,24	841,0	144,0
	12,0	8,1	30,0	97,2	360,0	243,0	65,61	900,0	144,0
	12,0	8,5	31,0	102,0	372,0	263,5	72,25	961,0	144,0
	14,0	9,6	32,0	134,4	448,0	307,2	92,16	1024,0	196,0
	14,0	9,0	36,0	126,0	504,0	324,0	81,0	1296,0	196,0
Сумма		123,8		1276,3		2997,4	837,74	10828,0	1958,0
Ср. знач.	9,6	6,19	22,3	63,815	229,05	149,87	41,887	541,4	97,9

Найдем средние квадратические отклонения признаков:

;

;

.

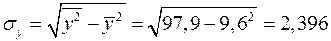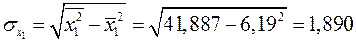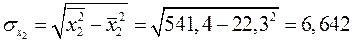1. Вычисление параметров линейного уравнения множественной регрессии.

Для нахождения параметров линейного уравнения множественной регрессии

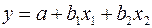
необходимо решить следующую систему линейных уравнений относительно неизвестных параметров , , :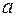

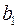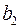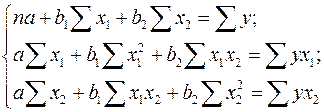
либо воспользоваться готовыми формулами:

; ;

.

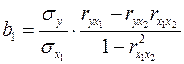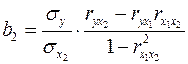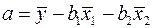Рассчитаем сначала парные коэффициенты корреляции:

;

;

.

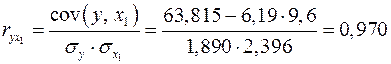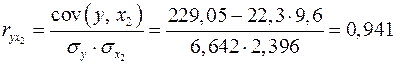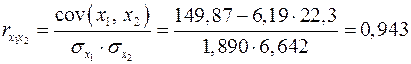Находим

;

;

.

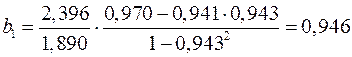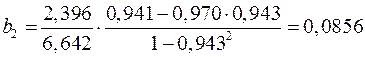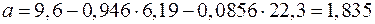Таким образом, получили следующее уравнение множественной регрессии:

.

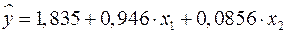Коэффициенты 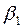и 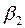стандартизованного уравнения регрессии 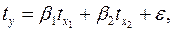находятся по формулам:

;

.

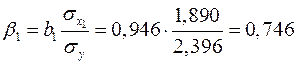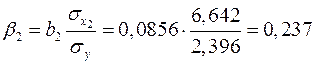Т.е. уравнение будет выглядеть следующим образом:

.

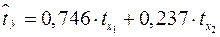Так как стандартизованные коэффициенты регрессии можно сравнивать между собой, то можно сказать, что ввод в действие новых основных фондов оказывает большее влияние на выработку продукции, чем удельный вес рабочих высокой квалификации.

Сравнивать влияние факторов на результат можно также при помощи средних коэффициентов эластичности:

.

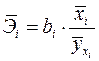Вычисляем:

; .

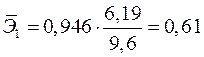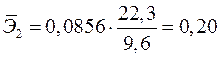Т.е. увеличение только основных фондов (от своего среднего значения) или только удельного веса рабочих высокой квалификации на 1% увеличивает в среднем выработку продукции на 0,61% или 0,20% соответственно. Таким образом, подтверждается большее влияние на результат фактора , чем фактора .

2. Коэффициенты парной корреляции мы уже нашли:

; ; .

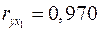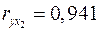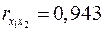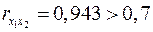Они указывают на весьма сильную связь каждого фактора с результатом, а также высокую межфакторную зависимость (факторы и явно коллинеарны, т.к. ). При такой сильной межфакторной зависимости рекомендуется один из факторов исключить из рассмотрения.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

При двух факторах частные коэффициенты корреляции рассчитываются следующим образом:

;

.

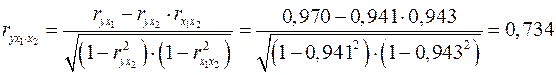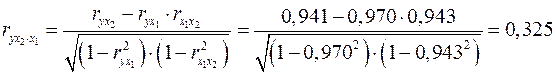Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за высокой межфакторной зависимости коэффициенты парной корреляции дают завышенные оценки тесноты связи. Именно по этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

Коэффициент множественной корреляции определить через матрицу парных коэффициентов корреляции:

,

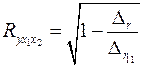где

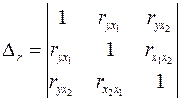
– определитель матрицы парных коэффициентов корреляции;

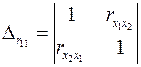
– определитель матрицы межфакторной корреляции.

;

.

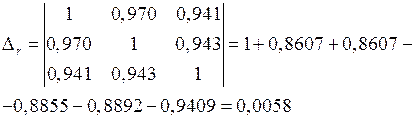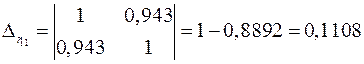Коэффициент множественной корреляции

.

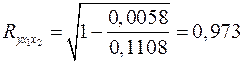Аналогичный результат получим при использовании других формул:

;

;

.

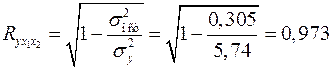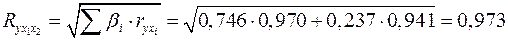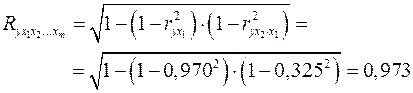Коэффициент множественной корреляции показывает на весьма сильную связь всего набора факторов с результатом.

3. Нескорректированный коэффициент множественной детерминации 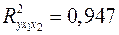оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 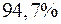и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов, иными словами – на весьма тесную связь факторов с результатом.

Скорректированный коэффициент множественной детерминации

определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую (более 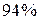) детерминированность результата в модели факторами и .

4. Оценку надежности уравнения регрессии в целом и показателя тесноты связи 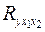дает 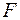-критерий Фишера:

.

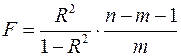В нашем случае фактическое значение 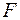-критерия Фишера:

.

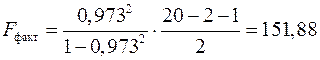Получили, что 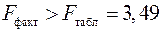(при 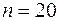), т.е. вероятность случайно получить такое значение 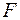-критерия не превышает допустимый уровень значимости 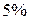. Следовательно, полученное значение не случайно, оно сформировалось под влиянием существенных факторов, т.е. подтверждается статистическая значимость всего уравнения и показателя тесноты связи .

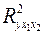5. С помощью частных 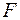-критериев Фишера оценим целесообразность включения в уравнение множественной регрессии фактора после и фактора после при помощи формул:

;

.

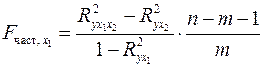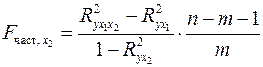Найдем 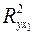и .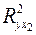

;

.

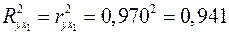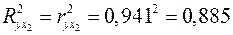Имеем

;

.

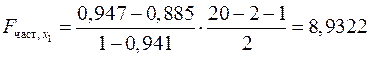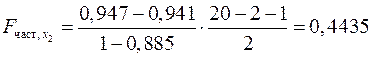Получили, что . Следовательно, включение в модель фактора после того, как в модель включен фактор статистически нецелесообразно: прирост факторной дисперсии за счет дополнительного признака оказывается незначительным, несущественным; фактор включать в уравнение после фактора не следует.

Если поменять первоначальный порядок включения факторов в модель и рассмотреть вариант включения после , то результат расчета частного 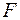-критерия для будет иным. 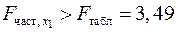, т.е. вероятность его случайного формирования меньше принятого стандарта 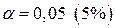. Следовательно, значение частного 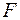-критерия для дополнительно включенного фактора не случайно, является статистически значимым, надежным, достоверным: прирост факторной дисперсии за счет дополнительного фактора является существенным. Фактор должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора .

6. Общий вывод состоит в том, что множественная модель с факторами и с 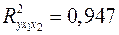содержит неинформативный фактор . Если исключить фактор , то можно ограничиться уравнением парной регрессии:

, .

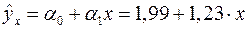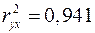Варианты индивидуальных заданий

По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих (%) (смотри таблицу своего варианта).

Требуется:

1. Построить линейную модель множественной регрессии. Записать стандартизованное уравнение множественной регрессии. На основе стандартизованных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.

2. Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.

3. Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентом детерминации.

4. С помощью 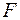-критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации .

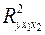5. С помощью частных 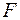-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора после .

6. Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.

Вариант 1

Номер предприятия				Номер предприятия
		3,6				6,3
		3,6				6,4
		3,9
		4,1				7,5
		3,9				7,9
		4,5				8,2
		5,3
		5,3				8,6
		5,6				9,5
		6,8

Вариант 2

Номер предприятия				Номер предприятия
		3,5				6,3
		3,6				6,4
		3,9
		4,1				7,5
		4,2				7,9
		4,5				8,2
		5,3				8,4
		5,3				8,6
		5,6				9,5

Вариант 3

Номер предприятия				Номер предприятия
		3,7				6,3
		3,7				6,4
		3,9				7,2
		4,1				7,5
		4,2				7,9
		4,9				8,1
		5,3				8,4
		5,1				8,6
		5,6				9,5
		6,1				9,5

Вариант 4

Номер предприятия				Номер предприятия
		3,5				6,3
		3,6				6,5
		3,9				7,2
		4,1				7,5
		4,2				7,9
		4,5				8,2
		5,3				8,4
		5,5				8,6
		5,6				9,5
		6,1				9,6

Вариант 5

Номер предприятия				Номер предприятия
		3,6				6,3
		3,6				6,9
		3,7				7,2
		4,1				7,8
		4,3				8,1
		4,5				8,2
		5,4				8,4
		5,5				8,8
		5,8				9,5
		6,1				9,7

Вариант 6

Номер предприятия				Номер предприятия
		3,5				6,3
		3,6				6,8
		3,8				7,2
		4,2				7,9
		4,3				8,1
		4,7				8,3
		5,4				8,4
		5,6				8,8
		5,9				9,6
		6,1				9,7

Вариант 7

Номер предприятия				Номер предприятия
		3,8				6,8
		3,8				7,4
		3,9				7,8
		4,1				7,5
		4,6				7,9
		4,5				8,1
		5,3				8,4
		5,5				8,7
		6,1				9,5
		6,8				9,7

Вариант 8

Номер предприятия				Номер предприятия
		3,8				7,1
		4,1				7,5
		4,3				7,8
		4,1				7,6
		4,6				7,9
		4,7				8,1
		5,3				8,5
		5,5				8,7
		6,9				9,6
		6,8				9,8

Вариант 9

Номер предприятия				Номер предприятия
		3,9				7,1
		4,2				7,5
		4,3				7,8
		4,4				7,9
		4,6				8,1
		4,8				8,4
		5,3				8,6
		5,7				8,8
		6,9				9,6
		6,8				9,9

Вариант 10

Номер предприятия				Номер предприятия
		3,6				7,2
		4,1				7,6
		4,3				7,8
		4,4				7,9
		4,5				8,2
		4,8				8,4
		5,3				8,6
		5,6				8,8
		6,7				9,2
		6,9				9,6

Дата добавления: 2014-10-15