В заданный интервал

Вероятность попадания случайной величины

Плотность распределения.

Непрерывная случайная величина.

Определение. Непрерывной случайной величиной Х, заданной на некотором интервале 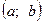или 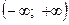,называется такая случайная величина, которая может принимать в результате серии испытаний любое значение из интервала 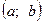или .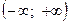

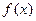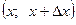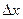Определение. Плотностью распределения вероятностей непрерывной случайной величины называется предел отношения вероятности попадания значения непрерывной случайной величины в интервал к при 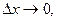если такой предел существует:

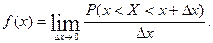
Свойства плотности распределения:

1. Плотность распределения неотрицательна, т. е.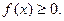

2. Несобственный интеграл от плотности распределения в пределах от 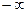до 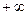равен единице:

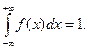
В частности, если все возможные значения непрерывной случайной величины 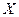находятся в интервале 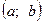, то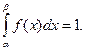

Определение. Функция распределения вероятностей 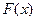непрерывной случайной величины 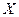равна несобственному интегралу от плотности распределения 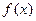с переменным верхним пределом:

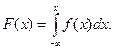(3.28)

Исходя из выше изложенного, плотность вероятности можно определить как первую производную от функции распределения:

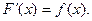(3.29)

Теорема. Пусть 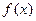− плотность распределения вероятностей непрерывной случайной величины 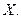Тогдавероятность попадания значения случайной величины 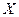в интервал равна определенному интегралу от функции 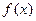в пределах от 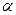до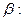

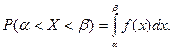(3.30)

Пример 3.47. Дана функция распределения непрерывной случайной величины Х:

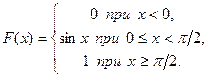
Найти плотность распределения

Плотность распределения равна первой производной от функции распределения:

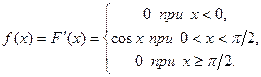
Заметим, что при 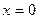производная 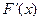не существует.

Пример 3.48. Дана плотность распределения непрерывной случайной величины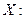

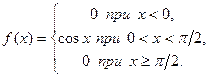
Найти функцию распределения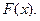

Используем формулу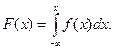

Если 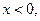то 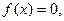следовательно,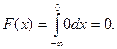

Если 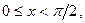то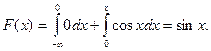

Если 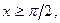то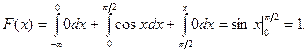

Таким образом, функция распределения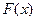имеет вид:

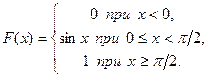
Пример 3.49. Дана плотность распределения непрерывной случайной величины Х:

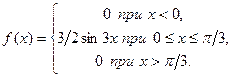
Найти вероятность того, что непрерывная случайная величина 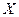примет значение из интервала .

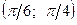Воспользуемся формулой (3.30):

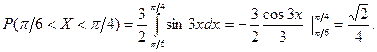
Дата добавления: 2014-10-15