Основные понятия математической статистики

Основные задачи математической статистики

Элементы математической статистики

В результате экономических, социологических, политологических и других исследований получают большие массивы статистических данных. Например, изучают распределение студентов первого курса г. Омска по росту (весу, состоянию здоровья, успеваемости и т. д.). Практически любой признак поддается непосредственному измерению либо может получить условную числовую характеристику. При этом некоторый признак элементов совокупности можно рассматривать как случайную величину, принимающую те или иные числовые значения с определенной вероятностью. В реальных исследованиях вероятность случайной величины оценивается с помощью ее относительной частоты при достаточно большом числе испытаний.

1. Определение методов сбора и группировки статистических сведений, полученных в результате экспериментов или наблюдений.

2. Разработка методов анализа статистических данных: оценка неизвестной вероятности, оценка зависимости случайной величины от других случайных величин и др.

Определение. Генеральной совокупностью называется совокупность всех элементов, обладающих интересующими исследователей признаками.

Определение. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных элементов из генеральной совокупности.

Определение. Объемом совокупности называется количество элементов, содержащихся в этой совокупности. Например, если из 2000 изделий отобрано для обследования случайным образом 100 изделий, то объем генеральной совокупности N = 2000, а объем выборки n = 100.

Определение. Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности. Пусть из генеральной совокупности извлечена выборка объема n, в которой значение x₁ некоторого исследуемого признака X (размер одежды, заработная плата и пр.) наблюдалось n₁ раз, значение x₂ − n₂ раз, …, значение x_k − n_k раз.

Определение. Значения x_i (i = 1, 2, 3, …, k)исследуемого признака X называются вариантами, а их последовательность, записанная в возрастающем порядке, − вариационным рядом.

Определение. Число n_i, показывающее сколько раз наблюдалось значение x_i некоторого признака X в исследуемой совокупности, называется частотой.

Определение. Отношение частоты значения x_i некоторого признака X в исследуемой совокупности к объему выборки n называется относительной частотой:

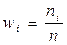. (3.38)

Необходимо отметить, что всегда выполняются равенства:

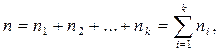(3.39)

(3.40)

Определение. Размах выборки (обозначается 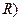− разность между максимальным и минимальным значениями случайной величины, полученными при исследовании выборки или длина интервала, которому принадлежат все значения варианты выборки:

.

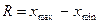Определение. Мода (обозначается – наиболее часто встречающееся значение случайной величины (исследуемого признака), полученное при исследовании выборки.

Определение. Ломаная, отрезки которой соединяют точки с координатами (х_i; n_i), где х_i – числовые значения исследуемого признака, а n_i – частота их появления в выборке, называется полигоном частот.

Наряду с полигоном частот можно построить полигон относительных частот, для этого по оси ординат необходимо откладывать относительные частоты .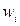

Определение. Гистограмма частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служатчастичные интервалы длины h, а высоты равны отношению 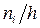(плотность частоты).

Площадь частичного i -го прямоугольника равна сумме частот, попавших в i -й интервал. Площадь гистограммы частот равна сумме всех частот, т. е. объему выборки n.

Определение. Гистограмма относительных частот – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служатчастичные интервалы длины h, а высоты равны отношению (плотность относительной частоты).

Площадь частичного i -го прямоугольника равна относительной частоте вариант, попавших в i -й интервал. Площадь гистограммы относительных частот равна единице.

Пример 3.55. Пусть исследуемый признак X – размер обуви мальчиков 9-х классов одной из школ имеет следующее распределение по частотам, представленное в виде таблицы 3.10.

Таблица 3.10

Распределение случайной величины по частотам

хi – размер обуви
ni− частота (количество учеников, имеющих определенный размер обуви)
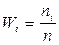− относительная частота

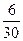
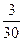
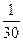
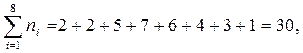
Размах и мода соответственно равны: 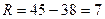и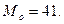

Дата добавления: 2014-10-15