Интервальные оценки параметров распределения

Определение. Интервальной называют оценку, которая определяется двумя числами − концами интервала, покрывающего оцениваемый параметр.

Определение. Доверительным называют интервал, который с заданной надежностью покрывает заданный интервал.

Интервальные оценки параметров нормального распределения:

1. Интервальной оценкой (с надежностью математического ожидания нормально распределенного количественного признака по выборочной средней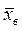служит доверительный интервал:

а) при известном среднем квадратическом отклонении 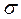генеральной совокупности

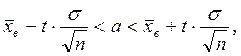(3.41)

где − точность оценки;

− объем выборки;

− значение аргумента функции Лапласа 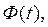при котором

б) при неизвестном среднем квадратическом отклонении 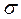генеральной совокупности

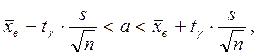(3.42)

где 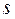− «исправленное» выборочное среднее квадратическое отклонение;

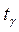− находятся по таблице приложения 2 по заданным и

2. Интервальной оценкой (с надежностью среднего квадратического отклонения 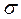нормально распределенного количественного признака по «исправленному» выборочному среднему квадратическому отклонению 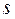служит доверительный интервал:

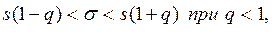(3.43)

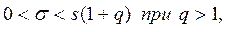
где находятся по таблице приложения 4 по заданным и

Пример 3.57. Найти доверительный интервал для оценки математического ожиданиянормально распределенного количественного признака надежностью 0,95, если генеральное среднее квадратическое отклонение 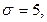выборочное среднее а объем выборки

Доверительный интервал найдем по формуле (3.43). Все величины известны, кроме 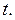Значение найдем из соотношения и затем находим по таблице приложения 4. Подставив все известные значения в формулу, получим искомый доверительный интервал 12,04 15,96.

Пример 3.58. По данным выборки объема из генеральной совокупности найдено «исправленное» выборочное среднее квадратическое отклонение S=1 нормально распределенного количественного признака X. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение 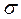с надежностью 0,95.

По данным задач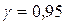и и в таблице приложения 4 найдем 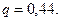Поскольку 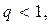то используя формулу (3.43) найдем искомый интервал

Дата добавления: 2014-10-15