Выборочный метод. ( Математическая статистика )

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Г

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

БОГДАНОВ А. Е.

(лекции)

(МК 2)

(Математическая статистика)

Задача математической статистики – создание методов сбора и обработки статистических данных для получения научных и практических выводов.

Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты.

Пример. □ Если имеется партия деталей, то качественным признаком может быть стандартность детали, а количественным признаком – контролируемый размер детали. ■

Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.

Генеральной совокупностью называют совокупность объектов, из которой произведена выборка.

Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности.

Пример. □ Если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки п = 100. ■

Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность.

Бесповторной называют выборку, при которой отобранный объект не возвращается в генеральную совокупность.

Для того, чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли, т.е. выборка должна быть репрезентативной (представительной).

Способы отбора:

1. отбор, не требующий расчленения генеральной совокупности на части:

а) простой (объекты извлекают по одному из всей генеральной совокупности) случайный бесповторный отбор;

б) простой случайный повторный отбор;

2. отбор, при котором генеральная совокупность разбивается на части:

а) типический отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее “типической” части;

б) механический отбор, при котором генеральную совокупность “механически” делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект;

в) серийный отбор, при котором объекты отбирают из генеральной совокупности не по одному, а “сериями”, которые подвергают сплошному обследованию.

На практике часто используют комбинированный отбор, при котором сочетаются перечисленные ранее отборы.

Статистическое распределение выборки

Пусть из генеральной совокупности извлечена выборка, при этом значение х ₁ наблюдалось п ₁ раз, х ₂ – п ₂ раз, …, х_k – п_k раз и 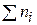= п – объем выборки.

Наблюдаемые значения х_i называют вариантами, а последовательность вариант, записанных в возрастающем порядке – вариационным рядом.

Числа наблюдений п_i называют частотами, а их отношения к объему выборки = w_i – относительными частотами.

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.

Пример. На телефонной станции исследовался дискретный количественный признак Х – число неправильных соединений за четверть часа (15 мин.). Наблюдения в течение двух часов дали следующие результаты:

3, 1, 3, 1, 0, 2, 4, 2.

Составить распределения частот и относительных частот полученной выборки.

□

Запишем вариационный ряд

0, 1, 1, 2, 2, 3, 3, 4.

Распределение частот выборки имеет вид

х_i 0 1 2 3 4

n_i 1 2 2 2 1.

Найдем распределение относительных частот.

Известно, что w_i = . Найдем объем выборки п =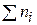= 1 + 2 + 2 + 2 + 1= 8. Тогда

w ₁ = 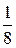= 0,125; w ₂ = = 0,25; w ₃ = = 0,25; w ₄ = = 0,25; w ₅ = 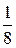= 0,125.

Распределение относительных частот:

х_i 0 1 2 3 4

w_i 0,125 0,25 0,25 0,25 0,125.

К о н т р о л ь:

=0,125+0,25+0,25+0,25+0,125 = 1.

Объем генеральной совокупности: так как в течение часа проводится четыре наблюдения, то за сутки (24 час.) имеем

N = 4·24 = 96.

■

Если количество вариант х слишком велико или близко к объему выборки, х_max − х_min ≥ 20 или рассматривается непрерывный признак генеральной совокупности, то статистическое распределение можно задать в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал). Все интервалы выбирают одинаковой длины таким образом, чтобы х_min вошло в первый, а х_max – в последний интервал. Обычно начало интервала входит в интервал, а его конец – не входит.

Эмпирическая функция распределения

Пусть известно статистическое распределение частот количественного признака Х. Введем обозначения: п_х – число наблюдений, при которых наблюдалось значение признака, меньшее х; п – общее число наблюдений (объем выборки).

Тогда относительная частота события Х < x будет равна 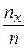. Если х изменяется, то и частота изменяется, т.е. она является функцией: 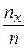= . Так как эта функция находится эмпирическим (опытным, экспериментальным) путем, то ее называют эмпирической.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию , определяющую для каждого значения х относительную частоту события Х < x:

= ,

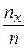где п_х – число вариант, меньших х; п – объем выборки.

Функцию распределения генеральной совокупности называют теоретической функцией распределения.

Эмпирическая функция распределения выборки служит оценкой (приближенным значением) теоретической функции распределения генеральной совокупности .

Функция обладает всеми свойствами функции :

1). значения функции принадлежат отрезку [0, 1];

2). − неубывающая функция;

3). если х ₁ – наименьшая варианта, то = 0 при х ≤ х ₁; если х_k − наибольшая варианта, то = 1 при х > х_k.

Эмпирическую функцию распределения можно вычислить по формуле:

Пример. Построить эмпирическую функцию по данному распределению выборки

х_i 2 6 10

n_i 12 18 30.

□

Найдем объем выборки п = :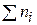

п = 12 + 18 + 30 = 60.

Найдем значения искомой функции на всех интервалах:

х ≤ 2: = 0;

2 < x ≤ 6: = = 0,2;

6 < x ≤ 10: = = 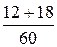= 0,5;

x > 10: = 1

или

Построим график эмпирической функции распределения:

■

Полигон и гистограмма

Для наглядности строят графики статистического распределения: полигон и гистограмму.

Полигоном частот называют ломаную, отрезки которой соединяют точки (х ₁, п ₁), (х ₂, п ₂), …, (х_k, п_k).

Для построения полигона частот на оси абсцисс откладываются варианты х_i, а на оси ординат – соответствующие им частоты n_i. Точки (х_i, п_i) соединяются отрезками прямых и получают полигон частот.

Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (х ₁, w ₁), (х ₂, w ₂), …, (х_k, w_k).

Построение аналогичное.

Пример. Построить полигон относительных частот по заданному распределению

х_i 1,5 3,5 5,5 7,5

w_i 0,1 0,2 0,4 0,3.

□

Полигон относительных частот имеет вид

■

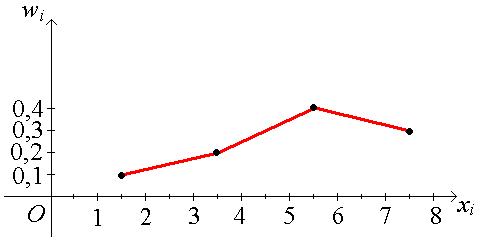
В случае непрерывного признака целесообразно строить гистограмму. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала п_i – сумму частот вариант, попавших в i -й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению 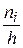(плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии .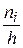

Площадь i -го частичного прямоугольника равна h ·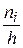= п_i, т.е. равна сумме частот вариант i -го интервала. Следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению (плотность относительной частоты).

Построение аналогичное.

Площадь i -го частичного прямоугольника равна h ·= w_i, т.е. равна относительной частоте вариант, попавших в i -й интервал.

Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. равна единице.

Пример. Построить гистограмму относительных частот по данному распределению выборки непрерывного признака

х_i 0 1 2 3 4 5

n_i 7 8 10 15 20 20

□

Разобьем интервал 0 – 5 на частичные интервалы [ х_i, х_{i +1}); i = 1, 2,…, т.

Пусть h = 2, тогда получим интервалы 0 – 2, 2 – 4, 4 – 6.

Построим таблицу

Номер интервала, i	Частичный интервал, [ xi, xi +1)	Сумма частот вариант частичного интервала, пi
	0 – 2 2 – 4 4 – 6

Найдем объем выборки:

п = 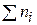= 15 + 25 + 40 = 80.

Найдем относительные частоты для каждого частичного интервала, учитывая, что w_i = :

w ₁ = 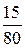= 0,1875; w ₂ = = 0,3125; w ₃ = = 0,5.

Найдем плотность относительной частоты, учитывая, что h = 2 и :

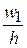= = 0,09375; = = 0,15625; = = 0,25.

Строим гистограмму

■

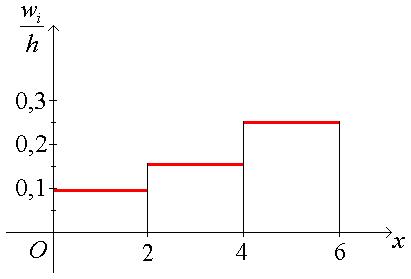
Дата добавления: 2014-10-15