Статистические оценки параметров распределения

Точечные оценки

Пусть требуется изучить количественный признак Х генеральной совокупности. Предположим, что из теоретических соображений удалось установить вид распределения признака. Возникает задача оценки параметров этого распределения. Например, если известно, что изучаемый признак распределен в генеральной совокупности по нормальному закону, то необходимо оценить (приближенно найти) математическое ожидание а и среднее квадратическое отклонение 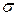, так как эти два параметра определяют нормальное распределение.

Обычно в распоряжении исследователя имеются лишь данные выборки х ₁, х ₂, …, х_п, полученные в результате п независимых наблюдений. Через эти данные и выражают оцениваемый параметр. В этом случае х ₁, х ₂, …, х_п рассматривают как независимые случайные величины Х ₁, Х ₂, …, Х_п.

Тогда статистической оценкой неизвестного параметра теоретического распределения называют функцию 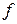(Х ₁, Х ₂, …, Х_п) от наблюдаемых случайных величин Х ₁, Х ₂, …, Х_п.

Точечной называют статистическую оценку, которая определяется одним числом = 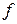(х ₁, х ₂, …, х_п), где х ₁, х ₂, …, х_п – результаты п наблюдений над количественным признаком Х (выборка).

Для того, чтобы статистические оценки давали “хорошие” приближения оцениваемых параметров, они должны удовлетворять определенным требованиям.

Пусть − статистическая оценка неизвестного параметра теоретического распределения. Допустим, что по выборке объема п найдена оценка 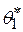. Повторим опыт, т.е. извлечем из генеральной совокупности выборку того же объема и по ее данным найдем оценку и т.д. В результате получим последовательность чисел 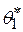, , …, 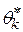. Таким образом, оценку можно рассматривать как случайную величину, а числа 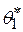, , …, 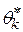− как ее возможные значения.

Предположим, что оценка дает приближенное значение с избытком. Тогда > , i = 1, 2, …, k. Значит и М () > . Очевидно, что если дает оценку с недостатком, то М () < . Использование таких оценок приводит к систематическим (одного знака) ошибкам. Требование М () = гарантирует от получения таких ошибок.

Несмещенной называют статистическую оценку , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т.е.

М () = .

Смещенной называют статистическую оценку, математическое ожидание которой не равно оцениваемому параметру.

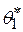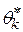Так как при выполнении условия М () = разброс оценок , , …, может быть велик, то необходимо потребовать, чтобы D () была мала.

Эффективной называют статистическую оценку, которая (при заданном объеме выборки п) имеет наименьшую возможную дисперсию.

При рассмотрении выборок большого объема к статистическим оценкам предъявляется требование состоятельности.

Состоятельной называют статистическую оценку, которая при п → ∞ стремится по вероятности к оцениваемому параметру, т.е.

− | < ε) = 1

или

.

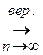
Генеральная средняя. Выборочная средняя. Дисперсия.

Пусть рассматривается генеральная совокупность относительно количественного признака Х.

Генеральной средней 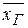называют среднее арифметическое значений признака генеральной совокупности.

Если все значения х ₁, х ₂, …, х_N признака генеральной совокупности объема N различны, то

= .

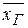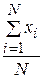Если значения признака х ₁, х ₂, …, х_k имеют соответствующие частоты N ₁, N ₂, …, N_k, причем N ₁ + N ₂ +…+ N_k = N, то

= .

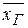Если рассматривать обследуемый признак Х генеральной совокупности как случайную величину, то

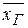= М (Х).

Это справедливо и для непрерывного распределения.

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема п.

Выборочной средней называют среднее арифметическое значений признака выборочной совокупности.

Если все значения х ₁, х ₂, …, х_п признака выборки объема п различны, то

= .

Если значения признака х ₁, х ₂, …, х_k имеют соответствующие частоты п ₁, п ₂, …, п_k, причем п ₁ + п ₂ +…+ п_k = п, то

= .

Выборочная средняя есть несмещенная оценка генеральной средней.

Так как 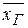= М (Х) признака Х, то за оценку математического ожидания генеральной совокупности можно взять :

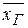≈ = М (Х).

Замечание 1. Если первоначальные варианты х_i – большие числа, то можно перейти к условным вариантам

и_i = х_i – C,

где С = const.

Обычно С выбирают равным одному из средних значений вариант. Тогда

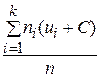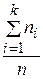= = С ·+ = С + = С + .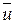

Генеральной дисперсией D_Г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения .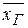

Если все значения х ₁, х ₂, …, х_N признака генеральной совокупности объема N различны, то

D_Г = .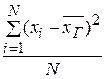

Если значения признака х ₁, х ₂, …, х_k имеют соответствующие частоты N ₁, N ₂, …, N_k, причем N ₁ + N ₂ +…+ N_k = N, то

D_Г = .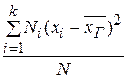

Генеральную дисперсию можно вычислить по формуле

D_Г = − ,

т.е. D_Г равна среднему квадратов значений признака генеральной совокупности минус квадрат генеральной средней.

Генеральным средним квадратическим отклонением (генеральным стандартом) называют квадратный корень из генеральной дисперсии

= .

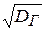Выборочной дисперсией D_В называют среднее арифметическое квадратов отклонений значений наблюдаемых значений признака от их среднего значения .

Если все значения х ₁, х ₂, …, х_п признака выборки объема п различны, то

D_В = .

Если значения признака х ₁, х ₂, …, х_k имеют соответствующие частоты п ₁, п ₂, …, п_k, причем п ₁ + п ₂ +…+ п_k = п, то

D_В = .

Выборочную дисперсию можно вычислить по формуле

D_В = −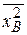

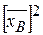
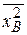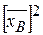или, если расписать и , то

D_В = − .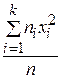

Замечание 2. Если первоначальные варианты х_i – большие числа, то можно перейти к условным вариантам (дисперсия при этом не изменяется)

и_i = х_i – C,

где С = const.

Тогда

D_В (Х) = D_В (и) = − = − .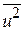

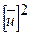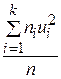Замечание 3. Если первоначальные варианты х_i являются десятичными дробями с k знаками после запятой, то можно перейти к условным вариантам (при этом дисперсия увеличится в С ² раз)

и_i = Сх_i,

где С = 10 ^k.

Тогда

D_В (Х) = .

Выборочным средним квадратическим отклонением (выборочным стандартом) называют квадратный корень из выборочной дисперсии

= .

Оценка генеральной дисперсии по исправленной выборочной дисперсии

Выборочная дисперсия D_В является смещенной оценкой генеральной дисперсии, при этом

М (D_В) = · D_Г.

Выборочную дисперсию можно “исправить” так, чтобы ее математическое ожидание было равно генеральной дисперсии. Для этого надо умножить D_В на дробь . В результате получим исправленную выборочную дисперсию, которая будет несмещенной оценкой генеральной дисперсии D_Г:

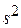= D_В = ·= .

Теперь

М (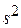) = М ( D_В) = М (D_В) = ·· D_Г = D_Г,

т.е. М (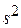) = D_Г и, значит, исправленная дисперсия 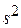является несмещенной оценкой D_Г.

Более удобная для расчетов формула

= .

В условных вариантах она имеет вид

= ,

причем если и_i = х_i – C, то = ; если и_i = Сх_i, то = .

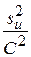Для оценки среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии

s = = .

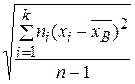Сравнивая формулы

D_В = и = ,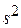

видно, что они отличаются только знаменателями. Очевидно, при достаточно больших значениях п объема выборки выборочная и исправленная дисперсии различаются мало. На практике пользуются исправленной дисперсией, если, примерно, п < 30.

Пример. Дано распределение выборки

х_i 1 2 3

n_i 2 1 4.

Найти несмещенные оценки генеральной средней, генеральной дисперсии, генерального среднего квадратического отклонения.

□

Несмещенной оценкой генеральной средней (и математического ожидания) является выборочная средняя .

Объем выборки: п = 2 + 1 + 4 = 7. Тогда

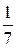= = ·(2·1 + 1·2 + 4·3) = 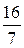≈ 2,29.

Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия .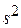

Имеем

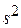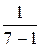= = ·(2(1− 2,29)² +1·(2 − 2,29)² + 4·(3 − 2,29)²) =

= ·(3,33 + 0,08 + 2,02) = 0,905.

Несмещенной оценкой генерального среднего квадратического отклонения является исправленное выборочное среднее квадратическое отклонение s.

Имеем

s = = ≈ 0,951.

■

Интервальные оценки

Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Интервальная оценка позволяет установить точность и надежность оценки.

Пусть служит оценкой неизвестного параметра . Оценка тем точнее определяет параметр , чем меньше абсолютная величина разности |− |. Другими словами, если некоторое число > 0 и |− | < , то, чем меньше , тем оценка точнее. Таким образом, положительное число характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка удовлетворяет неравенству |− | < . Можно только говорить о вероятности , с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки параметра по называют вероятность , с которой осуществляется неравенство |− | < .

Надежностью задаются заранее и ее значение близко к единице: 0,95; 0,99 и 0,999.

Пусть вероятность того, что |− | < равна :

Р (|− | < ) = .

Тогда

Р (−< − < ) =

или

Р (−< < +) = .

Это соотношение следует понимать так: вероятность того, что интервал (−, +) заключает в себе (покрывает) неизвестный параметр , равна .

Доверительным называют интервал (−, +), который покрывает неизвестный параметр с заданной надежностью .

Интервальной оценкой (с надежностью ) математического ожидания а нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении 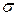генеральной совокупности служит доверительный интервал

− < a < + ,

где = − точность оценки, п – объем выборки, t – значение аргумента функции Лапласа Φ (t), при котором Φ (t) = ;

при неизвестном 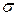(и объеме выборки п < 30)

− < a < +,

где s – исправленное выборочное среднее квадратическое отклонение, − определяют по таблице по заданным п и .

Интервальной оценкой (с надежностью ) среднего квадратического отклонения 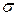нормально распределенного количественного признака Х по исправленному выборочному среднему квадратическому отклонению s служит доверительный интервал

s (1 − q) < 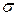< s (1 + q) (при q < 1),

0 < 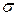< s (1 + q) (при q > 1),

где q = q (п, ) − определяют по таблице по заданным п и .

Замечание 1. Из формулы = следует:

1. при возрастании объема выборки п число убывает. Значит, точность оценки увеличивается;

2. увеличение надежности оценки = 2 Φ (t) приводит к увеличению t (Φ (t) – возрастающая функция). Значит, возрастает , т.е. точность уменьшается.

Замечание 2. Если требуется оценить математическое ожидание а с наперед заданной точностью и надежностью , то минимальный объем выборки, который обеспечит эту точность, находят по формуле

п = .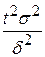

Пример. Найти доверительный интервал для оценки с надежностью = 0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если генеральное среднее квадратическое отклонение 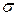= 5, выборочная средняя = 14 и объем выборки п = 25.

□

Требуется найти доверительный интервал

− < a < + .

Все величины, кроме t, известны. Найдем t из соотношения

Φ (t) = = = 0,475.

По таблице находим t = 1,96. Подставляем все значения в формулу доверительного интервала:

14 − 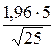< a < 14 +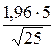

или

12,04 < a < 15,96.

Отметим смысл заданной надежности = 0,95. Надежность = 0,95 указывает, что если произведено достаточно большое число выборок, то 95% из них определяет такие доверительные интервалы, в которых неизвестный параметр (в нашем случае а)действительно заключен; лишь в 5% случаев он может выйти за границы доверительного интервала.

■

Пример. По данным 9 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений = 30,1 и исправленное среднее квадратическое отклонение s = 6. Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью = 0,99. Предполагается, что результаты измерений распределены нормально.

□

Истинное значение измеряемой величины равно ее математическому ожиданию а. Поэтому задача сводится к оценке математического ожидания (при неизвестном 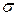) при помощи доверительного интервала

− < a < +.

По таблице находим

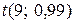= = 3,36.

Тогда

30,1− 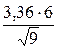< a < 30,1+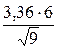

или

30,1− 6,72 < a < 30,1+ 6,72.

Следовательно,

23,38 < a < 36,82.

■

Пример. По данным выборки объема п = 16 из генеральной совокупности найдено исправленное среднее квадратическое отклонение s = 1 нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение 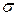с надежностью = 0,95.

□

Задача сводится к отысканию доверительного интервала

s (1 − q) < 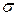< s (1 + q) (при q < 1)

или

0 < 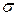< s (1 + q) (при q > 1).

По таблице находим

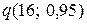= = 0,44 < 1.

Следовательно, используем интервал

s (1 − q) < 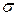< s (1 + q).

Тогда

1·(1 − 0,44) < 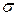<1·(1 + 0,44)

или

0,56 < 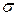<1,44.

■

Дата добавления: 2014-10-15