Фундаментальное уравнение адсорбции Гиббса

Адсорбция относится к поверхностным явлениям и протекает самопроизвольно. Концентрация веществ на поверхности раздела фаз происходит до достижения равновесия между процессами адсорбции и десорбции (см. рис. 4.1).

Для нахождения условий протекания самопроизвольного равновесного процесса обратимся к основам химической термодинамики. Адсорбция идет самопроизвольно, когда имеет место уменьшение энергии Гиббса, т.е. dG < 0. Согласно условию (2.1) для изобарно-изотермического процесса в отсутствие изменений площади поверхности раздела фаз и заряда поверхности (dТ = 0, dp = 0, dB = 0 и dq = 0) можно записать

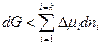. (4.6)

Для однокомпонентной системы получим

dG < Δμdn, или ΔG < ΔμΔn. (4.7)

Если обозначить химический потенциал i-гo компонента в объеме адсорбтива через (μ_i^V) и на поверхности адсорбента (μ_i^В), то согласно согласно (4.7) изменение энергии Гиббса определится по формуле

ΔG < (μ_i^B– μ_i^V)dn_i. (4.8)

Для самопроизвольных процессов (dG < 0) из условия (4.8) получим

μ_i^V> μ_i^B. (4.9)

Химический потенциал является фактором интенсивности любого физико-химического процесса, в том числе и адсорбции. Согласно условию (4.9) химический потенциал вещества в объеме μ_i^Vпревышает химический потенциал этого же вещества на поверхности μ_i^B.

Процесс адсорбции будет протекать до тех пор, пока будут достигнуты равновесные условия, т.е. до достижения состояния, когда ΔG = 0, что, согласно условию (4.8), соответствует равенству химических потенциалов адсорбтива и адсорбата (μ_i^V= μ^iB). В условиях равновесия скорости адсорбции и десорбции становятся равными.

На основании этого адсорбцию можно определить как процесс выравнивания химического потенциала, приводящего к росту концентрации компонентов на границе раздела фаз по сравнению с их концентрацией в объеме.

Для изобарно-изотермического процесса, когда dT = 0, dp = 0, dq = 0, с учетом всех компонентов системы в условиях равновесия (dG = 0) из уравнения (2.1) получим

μ_idn_i+ σdB = 0. (4.10)

Это уравнение связывает поверхностное натяжение с процессами, протекающими на границе раздела фаз. В нем экстенсивные величины стоят под знаком дифференциала (dn_iи dВ). Для однородной функции первой степени относительно экстенсивных величин можно воспользоваться теоремой Эйлера, которая позволяет интегрировать это уравнение при постоянных значениях коэффициентов интенсивных величин (μ_iи σ) при дифференциалах.

Напомним, что согласно теореме Эйлера любая однородная функция степени k, имеющая непрерывные частные производные, удовлетворяет равенству

f^/_x(x,y,z)x + f^/_y(x,y,z)y + f^/_z(x,y,z)z = kf(x,y,z).

Однородной называется функция, если при умножении всех ее аргументов на множитель она приобретает этот же множитель в k-й степени, т.е. f(tx₁,..., tx_m) = f^k(x₁,..., x_m).

Таким образом, если состав поверхностного слоя не изменяется, что соответствует конечному значению В и n_i, то можно записать

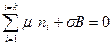. (4.10, a)

Полный дифференциал от всех переменных уравнения (4.10, а) выглядит так:

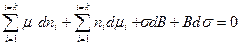. (4.11)

Из уравнения (4.11) вычтем уравнение (4.10), в результате получим

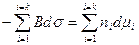. (4.12)

Используя уравнение (4.4) для выражения адсорбции, вместо формулы (4.12) можно записать

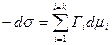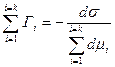; . (4.13)

Это уравнение называют фундаментальным уравнением адсорбции Гиббса.

В случае адсорбции только одного компонента уравнение (4.13) упрощается:

–dσ = Гdμ; Г = –dσ/dμ. (4.14)

Уравнения (4.13) и (4.14) справедливы для всех видов адсорбции; они показывают, что при адсорбции происходит самопроизвольное снижение удельной свободной поверхностной энергии (поверхностного натяжения) по мере изменения химического потенциала.

Адсорбция определяется избытком концентрации адсорбива с и обусловлена изменением поверхностного натяжения σ, которое зависит от температуры (см. параграф 2.3). Все величины, определяющие адсорбцию, взаимосвязаны, т.е. Г = f(c, σ, Т). Для нахождения этой зависимости воспользуемся уравнениями (4.13), в которых dσ характеризует уменьшение поверхностного натяжения в результате самопроизвольного процесса при адсорбции; Гiопределяет адсорбцию количественно, а dμ_iпоказывает возможность и интенсивность самопроизвольного процесса в результате изменения химического потенциала.

Используя уравнения (4.13), определим адсорбцию одного i-гo компонента из смеси веществ:

Г_i= – (д σ/ д μ_i)μ₁, …, μ_i–1, μ_i+1,..., μ_k. (4.15)

Адсорбция одного компонента i согласно условию (4.15) есть частная производная от поверхностного натяжения (удельной свободной поверхностной энергии) по изменению химического потенциала при постоянных химических потенциалах других компонентов.

Для нахождения химического потенциала воспользуемся следующим соотношением:

μ_i= μ_i⁰+ RTlnc, (4.16)

где μ_i, μ_i⁰– равновесный и стандартный химический потенциал адсорбтива; с – концентрация адсорбтива.

Если адсорбтив является сильным электролитом и его концентрация значительна, то вместо концентрации в этом уравнении следует использовать активность а.

Дифференцируя уравнение (4.16) и учитывая, что μ_i⁰есть величина постоянная, получим

dμ_i= RTdlnc = RT(dc/c). (4.17)

Заменив dμ_iв уравнении (4.13), подставив полученное выражение для dμ_iв уравнение (4.17), получим

Г = – (с/RT)(dσ/dc). (4.18)

Уравнение (4.18) непосредственно следует из фундаментального уравнения адсорбции Гиббса (4.14) и характеризует влияние на избыточную адсорбцию концентрации адсорбтива и температуры, а также изменение поверхностного натяжения (удельной свободной поверхностной энергии) в зависимости от концентрации адсорбтива. Оно справедливо для всех видов адсорбции.

Таким образом, уравнение (4.18) связывает между собой основные параметры, характеризующие адсорбцию (Г, с, Т и σ), и определяет результат самопроизвольного процесса за счет снижения поверхностного натяжения. Обычно рассматривают зависимость адсорбции от концентрации адсорбтива, что и будет использовано в дальнейшем.

Дата добавления: 2014-10-15