Дати повний економічний аналіз основних і додаткових змінних обох задач

Варіант	Ціна за одиницю продукції	Запаси сировини	Витрати сировини на кожен вид продукції
Р1	Р2
Р1	Р2	S1 В­2	S2	S3	S1 В­2	S2	S3	S1 В­2	S2	S3
201.
202.
203.
204.
205.
206.
207.
208.
209.
210.
211.
212.
213.
214.
215.
216.
217.
218.
219.
220.
221.
222.
223.
224.
225.
226.
227.
228.
229.
230.
231.
232.
233.
234.
235.
236.
237.
238.
239.
240.
241.
242.
243.
244.
245.
246.
247.
248.
249.
250.
251.
252.
253.
254.
255.
256.
257.
258.
259.
260.
261.
262.
263.
264.
265.
266.
267.
268.
269.
270.
271.
272.
273.
274.
275.
276.
277.
278.
279.
280.
281.
282.
283.
284.
285.
286.
287.
288.
289.
290.
291.
292.
293.
294.
295.
296.
297.
298.
299.
300.

ТРАНСПОРТНА ЗАДАЧА

У сучасній економіці велике значення мають задачі, пов’язані із транспортуванням вантажів, через те, що транспортування товарів від пунктів виробництва до пунктів їх реалізації вимагає великих витрат, що залежать від відстані, виду транспорту, маршрутів перевезень.

Транспортна задача (ТЗ) – це задача вибору оптимального варіанта доставки товару від пунктів виробництва до пунктів споживання з урахуванням усіх реальних можливостей. Використання розрахунків транспортної задачі, як правило, знижує витрати на 10-30%.

Розглянемо найпростішу класичну умову однопродуктової ТЗ з критерієм вартості.

Дано:

m – кількість пунктів виробництва деякого однорідного вантажу;

n – кількість пунктів призначення;

a_i – об’єм виробництва в і-му пункті, 1 ≤ i ≤ m (запаси);

b_j – об’єм споживання в j-му пункті, 1 ≤ j ≤ n (потреби).

c_ij – матриця затрат на перевезення одиниці вантажу із i-го пункту в j-й пункт споживання.

Смислова постановка задачі: скласти оптимальний план перевезень, тобто знайти скільки вантажу потрібно перевезти з кожного пункту відправлення у кожний пункт призначення так, щоб вартість перевезень була найменшою

Економіко-математична модель ТЗ: знайти такий план перевезень вантажів x­_ij, за яким витрати С на перевезення будуть мінімальні:

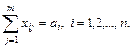за обмежень на обсяг виробництва і споживання вантажів, тобто виробництво вантажів в кожному пункті і повинно дорівнювати обсягу вивезеного вантажу:

Обсяг отриманого вантажу в пункті j повинен дорівнювати обсягу вивезеного вантажу з усіх пунктів виробництва в пункт j, тобто:

Обсяги перевезень вантажів повинні бути невід’ємними числами: x_ij ≥ 0, i = 1,2,…,n, j = 1,2,…,m.

Складемо транспортну таблицю (табл.1), в якій зліва в стовпці записуємо обсяг вантажів, які потрібно вивезти з кожного пункту виробництва. У верхньому рядку записуються обсяги споживання вантажів в місцях споживання. У правому верхньому кутку клітинки записується вартість перевезення одиниці вантажу, а в самій клітинці – обсяг перевезень вантажу.

Таблиця 1.

Наявність вантажу аі	Пункти споживання і обсяг споживання вантажу
b1	b2	…	bj	…	bm
a1	С11	X11	C12	X12	…	C1j	X1j	…	C1m	X1m
a2	С21	X21	C22	X22	…	C2j	X2j	…	C2m	X2m
…	…	…	…	…	…	…
ai	Сі1	Xi1	Ci2	Xi2	…	Cij	Xij	…	Cim	Xim
…	…	…	…	…	…	…
an	Cn1	Xn1	Cn2	Xn2	…	Cnj	Xnj	…	Cnm	Xnm

Для вирішення ТЗ необхідно і достатньо, щоб сума запасів вантажу в пунктах відправлення дорівнювала сумі потреб вантажу у пунктах призначення (закрита транспортна задача): А = а₁+ а₂+…+а_n = b₁+ b₂+…+b_m = B.

Якщо вказана умова не виконується, то отримуємо відкриту ТЗ, яку за допомогою перетворень зводимо до закритої.

Будь-який розв’язок задачі, який задовольняє вищевказані умови х_ij (i = 1,2,…,n, j = 1,2,…,m) називається допустимим планом транспортної задачі.

План х^*_ij (i = 1,2,…,n, j = 1,2,…,m) при якому витрати С на перевезення мінімальні, називається оптимальним планом транспортної задачі.

Продемонструємо відшукання оптимального плану ТЗ на конкретному прикладі.

Приклад 4.

Для транспортної задачі, вихідні дані якої наведені в таблиці 2, знайти оптимальний план.

Таблиця 2.

Наявність вантажу аі	Потреби в пунктах призначення bj

Розв’язання:

Дата добавления: 2014-10-15