Додавання багаторозрядних двійкових чисел лк-6

Лекція №3 Алгоритми виконання арифметичних операцій над двійковими числами

Тема 1.3 Виконання арифметичних операцій над двійковими числами

1. Додавання багаторозрядних двійкових чисел.

2. Алгебраїчне додавання з використанням оберненого коду. Алгебраїчне додавання з використанням модифікованого коду.

Додавання, віднімання і множення (арифметичне) однорозрядних двійкових чисел.

Додавання Віднімання Множення

При записі коду знак числа представляємо записаними у дужках цифрами 0 (для додатних чисел) та 1 (для від’ємних чисел).

1)

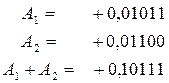
2)

У обчислювальній техніці операція віднімання замінюється операцією алгебраїчного додавання. При цьому використовуються спеціальні коди.

Наприклад: використовується доповнюючий код, який утворюється слідуючим чином, додатне число переписується без змін, а у від’ємному числі всі розряди крім знакового змінюються на протилежні, після чого у молодший розряд додається одиниця. І одержані числа додаються за правилами двійкової арифметики.

Приклад: Виконати операцію додавання двох чисел А1= - 36 та А2 = 163.

Перетворюємо числа в двійковий формат:

3) - 0010 0100 А1

1010 0011 А2

Інвертуємо А1 0010 0100→ 1101 1011.

Додаємо одиницю до молодшого розряду 1101 1011+0000 0001=1101 1100

Виконуємо додавання числа А2 та числа А1 у доповнюючому коді:

1010 0011 (163)

[phone] (доповнення числа -36)

А1+А2 1 0111 1111

Одиницю у дев’ятому біті необхідно відкинути від’ємне число більше (форма з фіксованою комою). Якщо результат додавання є від’ємне число, то він представлений у доповнюючому коді, для перетворення у прямий код інвертуємо результат та додаємо 1 до молодшого розряду.

4) А₁=+0,01011; А₂=-0,01100

А1=	(0)
А2=	(1)
					+
	(1)

доповнюючий код

А₁+А₂

	(0)
+	(1)
(А1+ А2)доп	(1)
інвертуємо, та додаємо 1					+
А1+А2	(1)

Результат:

А₁+А₂= -0,00001

5) Два від’ємні числа.

А₁= -0,00011 А₁=(1)11100₊₁ = (1)11101 доповнюючий код

А₂= -0,00001 А₂=(1)11110₊₁ = (1)11111

А₁+А₂

	(1)
+	(1)
Відкидаємо ® 1	(1)
або віднімаємо 1 та					-
інвертуємо результат	(1)

Результат:

А₁+А₂= -0,00100

Якщо А₁ має 4 розряди, то дописуємо 0.

А₁=-0,10010 А₁=(1)01101₊₁ = (1)01110

А₂=+0,01001 А₂= (0)01001 доповнюючий код

А₁+А₂

	(1)
+	(0)
	(1)
					-
	(1)

Результат: А₁+А₂= -0,01001

Крім доповнюючого коду є зворотній код в якому можуть бути виконане алгебраїчне додавання і модифікований код в якому теж може бути виконане алгебраїчне додавання.

Дата добавления: 2014-10-15