Лекция 11. Теплопроводность твердых тел. Закон Грюнайзена

Лекция 10. Ангармонизм колебаний атомов кристалла и тепловое расширение, среднее отклонение атома от положения равновесия, изменение электрического сопротивления при изменении температуры

В предыдущих лекциях было использовано гармоническое приближение, основной принцип которого – учет не выше второй производной по межатомным расстояниям при разложении потенциальной энергии системы взаимодействующих атомов U(r) в ряд Тейлора вблизи точки равновесия r=r₀. В гармоническом приближении закон Гука выполняется, а вот тепловое расширение необъяснимо. Кроме того, следствиями гармонического приближения, никогда точно не выполняющимися в твердых телах, являются: 1) равенство между собой адиабатических (постоянный объем) и изотермических (температура постоянна) упругих постоянных и их независимость от давления и температуры; 2) теплоемкость при высоких температурах перестает зависеть от температуры и C_p=C_V; 3) упругие волны в решетке не взаимодействуют друг с другом и со временем не изменяют свою форму. Учет производных третьего и более высокого порядков при разложении потенциальной энергии системы взаимодействующих атомов U(r) в ряд Тейлора вблизи точки равновесия соответствует ангармоническому приближению. Ангармонизм колебаний атомов приводит к зависимости частоты колебаний от амплитуды смещений, к описанию теплового расширения и взаимодействию фононов. В области низких температур, степень ангармонизма в решетке мала, фононная модель применима. Коэффициент фонон-фононного рассеяния m_ф-ф для модели взаимодействующих фононов, выражается соотношением

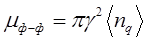
где 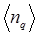− средняя плотность фононов, 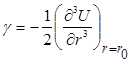– коэффициент ангармонизма. При учете ангармонизма при некоторой температуре отклонения атома от положения равновесия r₀ влево и вправо не равны и средние значения координат отличаются от равновесного r₀. Потенциальная энергия при увеличении r меняется медленнее, чем по гармоническому закону. Для описания теплового расширения твердого тела воспользуемся приближенной моделью, в которой решетка заменена на совокупность ангармонических осцилляторов, при этом в рассмотрении учитываем только первые три производные при разложении U(r) в ряд Тейлора вблизи точки равновесия r=r₀. В таком приближении среднее смещение атомов от положения равновесия 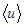при нагревании пропорционально температуре и коэффициенту ангармонизма g и обратно пропорционально квадрату коэффициента квазиупругой силы b, и выражается соотношением 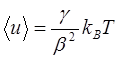. А относительное удлинение тела при нагревании равно 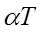, где коэффициент теплового расширения . Знак a определяется характером асимметрии потенциальной энергии U (r) вблизи положения равновесия. Если ветвь при r<r₀ меняется круче, чем при r>r₀, то при нагревании тело расширяется, если наоборот, то сжимается, если ветви симметричны, размеры тела не изменяются. Такой вид коэффициента теплового расширения справедлив для поликристаллических тел, для которых a - средний коэффициент линейного теплового расширения. Монокристаллы обладают анизотропией свойств, поэтому коэффициенты линейного расширения для различных направлений внутри монокристалла имеют как правило различные значения. У некоторых кристаллов при определенной температуре наблюдается отрицательное значение a по одной или двум из трех кристаллографических осей (т.е. всего выделяют 3 главных коэффициента теплового расширения монокристалла по 3-м кристаллографическим осям монокристалла). Отрицательное значение коэффициента линейного расширения означает, что такой кристалл при нагревании сжимается по этой оси.

Рассмотрим вклад электронов в теплоемкость. Согласно квантовой теории теплоемкость электронного газа: 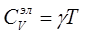, при этом g» 4×10^-4 Дж/(моль×К²). Таким образом, при комнатной температуре вклад электронов в полную теплоемкость мал по сравнению со значением решеточной теплоемкости, даваемым законом Дюлонга и Пти. При температурах ниже 4 К доля теплоемкости электронного газа в металлах 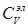превышает долю решеточной теплоемкости 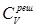, т.к. электронная теплоемкость уменьшается с температурой линейно, а решеточная − по закону T³. Однако при достаточно высоких температурах электронная теплоемкость ответственна за медленное линейное возрастание полной теплоемкости при высоких температурах, в то время как решеточная теплоемкость в этой области температур (выше температуры Дебая) уже практически не меняется. Большинство металлов плавится до того, как электронная теплоемкость достигнет заметной величины.

При увеличении температуры атомы металла увеличивают амплитуду колебаний около узлов решетки, увеличивается количество фононов, что вызывает увеличение рассеяния электронов на фононах и приводит к увеличению электрического сопротивления. При T ®0 электропроводность металлов стремиться к некоторому конечному значению, у ряда металлов возникает сверхпроводящее состояние, у диэлектриков и полупроводников электропроводность при T ®0 тоже стремиться к 0. Для диэлектриков и полупроводников (без примесей) с увеличением температуры все большее количество электронов может перейти из валентной зоны в зону проводимости, соответственно увеличивается и концентрация дырок, т.е. происходит рост числа носителей заряда, следовательно электрическое сопротивление падает.

Наличие инородных атомов (примесей или легирующих добавок) вызывает нарушение кристаллической решетки металла, что увеличивает электрическое сопротивление.

Зависимость электрического сопротивления от деформации можно выразить следующим образом: производная от сопротивления по температуре не зависит от деформации.

Тест

Вопрос 1 Учет производных какого порядка при разложении потенциальной энергии системы взаимодействующих атомов U(r) в ряд Тейлора вблизи точки равновесия соответствует гармоническому приближению.

Варианты ответов: до 1-ого; до 2-ого; до 3-его

Вопрос 2. Соответствует ангармоническому приближению

Варианты ответов: до 1-ого; до 2-ого; 3-его и выше

Вопрос 3. Возможно ли описание теплового расширения в гармоническом приближении

Варианты ответов: да, нет, частично

Вопрос 4. Как в ангармоническом приближении зависит относительное удлинение тела при нагревании от температуры

Варианты ответов: линейно, квадратично, по закону Т³, обратно пропорционально

Вопрос 5 Как ведет себя электрическое сопротивление металлов при увеличении температуры:

Варианты ответов: увеличивается, уменьшается, остается постоянным

Вопрос 6 Как ведет себя электрическое сопротивление полупроводников без примесей при увеличении температуры

Варианты ответов: увеличивается, уменьшается, остается постоянным

Вопросы для контроля:

1. Что нового по сравнению с гармоническим позволяет сделать ангармоническое приближение? (описать тепловое расширение, ввести зависимость частоты колебаний от амплитуды смещений, учесть взаимодействие фононов.)

2. Что означает эффект вымораживания фононов и к чему он приводит? (При понижении температуры происходит уменьшение плотности фононов- это явление называется эффектом вымораживания фононов, и оно приводит к уменьшению теплоемкости.)

3. Запишите выражение для среднего отклонения атома от положения равновесия в ангармоническом приближении.

4. Чему равен коэффициент теплового расширения?

5. Запишите выражение для коэффициента ангармонизма

6. Запишите выражение для теплоемкости электронного газа, как она соотносится с решеточной теплоемкостью, описать для низких, комнатных и высоких температур

7. Схематично изобразите зависимость потенциальной энергии взаимодействия между двумя атомами с учетом ангармонизма колебаний

8. Что означает отрицательный коэффициент теплового расширения по одной из трех кристаллографических осей монокристалла?

Теплопроводность - процесс переноса тепла от более нагретых частей тела к менее нагретым, приводящий к выравниванию температуры тела. В жидкостях и газах возможна конвекция - передача тепла потоками нагретого вещества, в твердых телах такой механизм не возможет и перенос тепла осуществляется за счет колебаний кристаллической решетки. Таким образом, исходя из квантово-механических представлений теплопроводность в твердых телах осуществляется за счет движения фононов. Закон теплопроводности Фурье можно записать в следующем виде:

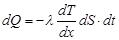
где dQ - тепловой поток через поперечное сечение стержня dS за время dt в зависимости от градиента температуры 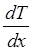, считается, что площадка dS перпендикулярна оси x, l - коэффициент теплопроводности (количество тепла, прошедшее через единицу площади за единицу времени при градиенте температуры, равном единице, единица измерения в СИ Вт/(м×К)). Знак минус в законе теплопроводности Фурье показывает, что распространение тепла идет от более нагретой части тела к более холодной, т.е. в сторону, противоположную градиенту температуры и способствует выравниванию градиента температуры.

При высоких температурах квантовый характер теплообмена не заметен, т.к. возбуждены практически все колебания в кристалле, энергии хватает для любых квантовых переходов. При низких температурах в кристалле возбуждены лишь колебания с малыми частотами, и за счет температуры не могут быть преодолены все квантовые переходы, поэтому при низких температурах квантовый характер теплообмена особенно заметен. Поэтому для диэлектриков (существенно, что фононы – превалирующие переносчики тепла) при низких температурах, используя из теории Дебая представления об идеальном газе фононов, можно получить, что коэффициент теплопроводности пропорционален теплоемкости единицы объема фононного газа, которая при приближении к 0 температур ведет себя по закону T³. Используя представления физической кинетики показано, что коэффициент теплопроводности диэлектриков обратно пропорционален температуре при температурах выше температуры Дебая.

Для качественного вывода закона Грюнайзена, который устанавливает одинаковую температурную зависимость удельной теплоёмкости C_V и коэффициента теплового расширения a_T твёрдых диэлектриков, введено понятие свободной энергии квазичастицы, для которой получено выражение

.

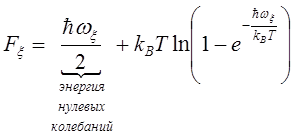Общепринятая запись закона Грюнайзена

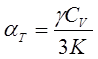
где К - модуль всестороннего сжатия, g - параметр Грюнайзена. Закон Грюнайзена соблюдается только в предположении одинаковой зависимости частот всех нормальных колебаний кристаллической решетки (фононных мод) от объёма V, т.е. 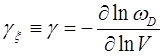(w_D- частота Дебая) и отсутствии температурной зависимости модуля всестороннего сжатия. В более широком смысле закон Грюнайзера является точным и формулируется как одинаковая температурная зависимость удельной теплоёмкости C_V и коэффициента теплового расширения a_T твёрдых тел в области достаточно низких температур, когда теплоёмкость твёрдого тела определяется всего одним типом длинноволновых возбуждений (квазичастиц).

В металлах в переносе тепла, кроме колебаний атомов кристаллической решетки, участвуют свободные электроны, вклад которых становится особенно заметен при повышении температуры.

Тест

Вопрос 1. По какому закону изменяется коэффициент теплопроводности диэлектриков при низких температурах

Варианты ответов: T³, T^-1, Т

Вопрос 2. По какому закону изменяется коэффициент теплопроводности диэлектриков при температурах выше температуры Дебая

Варианты ответов: T³, T^-1, Т

Вопрос 3

Параметр Грюнайзена записывается в виде:

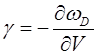
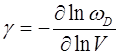
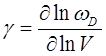
Вопросы для контроля

1. Сформулируйте закон Грюнайзена

2. При каких допущениях закон Грюнайзера является применимым?

3. Запишите выражение для свободной энергии через энтропию

4. Запишите выражение для свободной энергии через частоту колебаний

5. Запишите полное давление, создаваемое в кристалле за счет его колебаний в приближении Грюнайзена.

Дата добавления: 2014-10-15