Лекция 15 Движение электрона в металле в стационарном внешнем магнитном поле

Рассмотрено движение электрона в металле при воздействии постоянного внешнего магнитного поля. Учет внешнего магнитного поля в гамильтониане свободной частицы в импульсном представлении осуществляется следующим образом:

U(r) периодическом поле, оператор импульса, A(r) — векторный потенциал поля. Задача как мы видим, весьма непроста, однако, она заметно упрощается в случае достаточно слабого поля. При достаточно слабом внешнем магнитном поле применяется переход к квазиимпульсному представлению. Условие малости внешнего поля может быть сформулировано в общем виде как 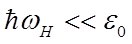, где ларморова частота (ларморова частота – это угловая частота прецессии магнитного момента, помещенного в магнитное поле), e₀ наименьшая из энергетических величин, характеризующих s-ую зонув которой находится электрон, — ее характерную ширину или расстояние до соседних зон (т. е. разностей 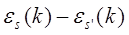) при заданных k, k –волновое число). Поэтому движение электрона в решетке в слабом магнитном поле описывается гамильтонианом (в К -представлении, где обобщенный импульс)

и имеется полная аналогия со способом введения магнитного поля в гамильтониан свободной частицы в импульсном представлении. Причем при медленно меняющемся в пространстве потенциале A(r) волновые функции «нулевого» (по напряженности поля Н) приближения будут

(причем функции и, благодаря переменности А, уже не являются строго периодическими, аналог – блоховские функции, но там u строго периодичны). Энергии же надо рассматривать теперь как операторы, образующие гамильтониан в K -представлении.

В квазиклассическом случае (условие малости изменения дебройлевской длины волны частицы на расстояниях порядка ее самой или в рассматриваемом случае: радиус кривизны орбиты велик по сравнению с дебройлеровской длиной волны) имеет смысл понятие траектории частицы

(индекс s для краткости опускаем).

Проведя некоторые математические преобразования получим уравнение движения, по виду напоминающее классическое уравнение Лоренца

(1)

Но отличающееся от него другой зависимостью e(k): вместо простой квадратичной функции здесь стоит сложная периодическая функция. Отсюда следует, что и v(k) сложная периодическая функция. В уравнении (1) Н – напряженность внешнего магнитного поля.

Рассмотрено движение электрона в металле в однородном магнитном поле, при котором e=const, k_z=const (ось z - в направлении поля Н). Геометрически траектория движения электрона в k -пространстве траектория представляет собой контур сечения изоэнергетической поверхности e(k) плоскостью, перпендикулярной магнитному полю. Изоэнергетические поверхности могут иметь самую разнообразную форму. Если движение происходит по замкнутым траекториям в квазиимпульсном пространстве, то оно периодично во времени с периодом движения

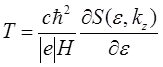
Где S(e,k_z) площадь сечения изоэнергетической поверхности e=const плоскостью k_z=const., при этом направление k_z совпадает с направлением внешнего магнитного поля H.

Вводится понятие циклотронной массы электрона в решетке

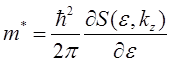
через которую выражается частота обращения электрона по орбите

Это выражение отличается от известной формулы для ларморовой частоты свободных электронов заменой их массы на . В случае электронов в решетке циклотронная масса не постоянная величина, а функция e и k_z так что она различна для разных электронов. Циклотронная масса может быть как положительной, так и отрицательной; в первом случае электрон движется по орбите как отрицательно заряженная частица, а во втором — как положительно заряженная частица — дырка. Поэтому говорят об электронных и дырочных траекториях.

Существует связь между траекториями в квазиимпульсном и обычном пространствах: напомним, как и ранее направление оси z совпадает с направлением внешнего магнитного поля, тогда xy -проекция орбиты в обычном пространстве повторяет k -траекторию, отличаясь от нее лишь ориентацией и масштабом. Траектория в обычном пространстве получается из траектории в k -пространстве заменой

В обычном пространстве также имеется движение вдоль оси z со скоростью 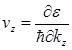. Заметим, что если траектория в k -пространстве замкнута, то в обычном пространстве она представляет собой спираль с осью вдоль направления поля. Если траектория k -пространстве открытая, то открыта также и проекция траектории на плоскости xy в обычном пространстве.

В лекции также рассмотрена вероятность пренебрегать явлением магнитного пробоя, т.е. перехода с одной траектории в k -пространстве на другую под действием внешнего магнитного поля. Вероятность перехода с одной траектории в k -пространстве на другую, не мала, если эти траектории где-либо подходят аномально близко друг к другу: траектория близка к траектории с самопересечением, либо если траектория проходит вблизи пересечения двух листов изоэнергетической поверхности (т. е. вблизи точки вырождения). В этом случае разрыв dk между траекториями мал по сравнению с характерными размерами орбит в целом, а радиус кривизны R_k траекторий вблизи точек их максимального сближения по порядку величины совпадает с dk. Вероятность магнитного пробоя экспоненциально мала, если dk велико по сравнению с расстоянием Dk_x на котором затухает волновая функция в классически недоступной области между траекториями 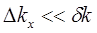. Это условие реализуется при , т.е. при выполнении этого условия явлением магнитного пробоя можно пренебречь.

Тест

Вопрос 1. Имеется ли аналогия между записью гамильтониана электрона в металле во внешнем слабом магнитном поле и способом введения магнитного поля в гамильтониан свободной частицы в импульсном представлении

Варианты ответов: да, нет.

Вопрос 2. Обобщенный импульс (квазиимпульс) записывается как

Варианты ответов:

Вопрос 3 При медленно меняющемся в пространстве потенциале A(r) волновые функции «нулевого» (по напряженности поля Н) приближения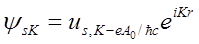

строго периодичные функции u или нет

Варианты ответов: строго периодичные, не являются строго периодическими

Вопрос 4. Основное отличие уравнения движения электрона в решетке во внешнем магнитном поле отличается от классического уравнения Лоренца

Варианты ответов: ничем не отличается, отличается видом функции e(k)

Вопрос 5. Как записывается периодом движения, если движение происходит по замкнутым траекториям в квазиимпульсном пространстве (учитывая, что S(e,k_z) площадь сечения изоэнергетической поверхности e=const плоскостью k_z=const., при этом направление k_z совпадает с направлением внешнего магнитного поля H)

Варианты ответов:

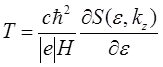
Вопрос 6. циклотронная масса электрона в решетке

Варианты ответов

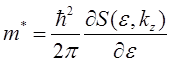
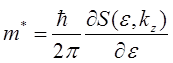
Вопрос 7. Может ли циклотронная масса электрона в решетке быть отрицательной

Варианты ответов: да, нет

Вопрос 8: Существует ли связь между траекториями в квазиимпульсном и обычном пространствах

Варианты ответов: да, нет

Дата добавления: 2014-10-15