Список тем, выносимых для решения в виде задач на семинарах

1. Вероятности распределения координат и импульсов классического гармонического осциллятора.

2. Температурное распределение вероятностей координат и импульсов классического осциллятора. Вывод закона Дюлогна и Пти в приближении сопоставления атому 3 гармонических осцилляторов

3. Спектр квантового осциллятора, переходы между уровнями. Учёт принципа неопределённости, энергия нулевых колебаний.

Задача 1. Найти среднеквадратичное смещение атома как одномерного гармонического осциллятора при тепловых колебаниях.

Указание. Энергия нулевых колебаний не несет тепловой нагрузки. Сопоставить классические и квантовые выражения для энергии гармонического осциллятора.

4. Среднее термодинамическое число колебательных квантов, распределение Планка и его предельные значения при низких и высоких температурах.

5. Температурное поведение тепловой энергии и теплоёмкости квантового осциллятора.

6. Энтропия квантового осциллятора, её температурное поведение и связь с процессом хаотизации движения

7. Уравнение состояния квантового осциллятора и температурное поведение создаваемого им давления.

Примеры задач по теме квантовый гармонический осциллятор с решениями:

Задача 1. Гармонический осциллятор находится в основном состоянии. Найдите вероятность обнаружения частицы вне пределов классической области, т.е. вне области –a₀£ x £a₀, где a₀ - амплитуда классических колебаний.

Решение: Поскольку осциллятор находится в основном состоянии, то, его энергия равна 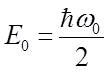, а волновая функция, описывающая его состояние, имеет вид 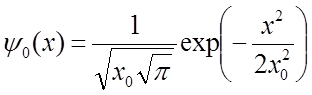. Здесь 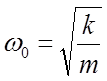- частота классического гармонического осциллятора, а параметр x₀ определяется выражением

.

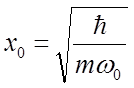При максимальном отклонении классического осциллятора от положения равновесия его полная энергия должна быть равна потенциальной энергии, т.е.

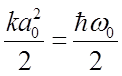
Отсюда следует, что амплитуда классических колебаний

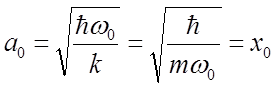
Найдем вероятность обнаружения частицы в классической области

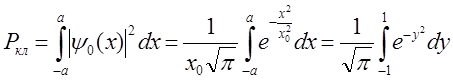
Где 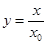. Поскольку под интегралом стоит четная функция переменной y, то

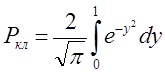
Интеграл

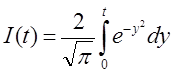
называется интегралом вероятностей. Этот интеграл широко используется в теории вероятностей, статистике, теоретической и математической физике, его значения для различных пределов интегрирования t приведены в таблицах. В данном случае, при t=1, I(1)»0.8427, следовательно

P_кл»0.8427=0.84

Соответственно, вероятность P того, что частица будет обнаружена вне классической области, равна

P=1- P_кл=0.16

Таким образом, вероятность пребывания гармонического осциллятора, находящегося в основном состоянии, вне пределов классической области составляет ~ 16 %, т.е. имеет заметную величину.

Задача 2. Квантовый гармонический осциллятор с частотой колебаний 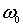находится в первом возбужденном состоянии. Найдите средние значения потенциальной <U> и кинетической <E_k> энергий осциллятора.

Решение: В силу того, что осциллятор находится в первом возбужденном состоянии, его энергия, согласно 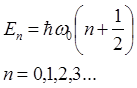, равна 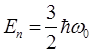, а соответствующая ему волновая функция имеет вид

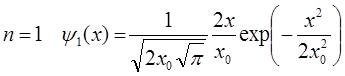
Где .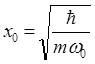

Операторы потенциальной 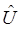и кинетической 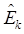энергий в рассматриваемой задаче есть

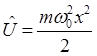и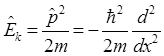

средние значения потенциальной <U> и кинетической <E_k> энергий осциллятора в состоянии, описываемом волновой функцией 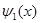, определяются выражениям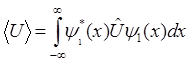и

и 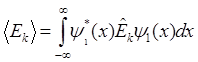эти записи идентичны записям

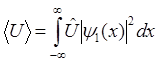и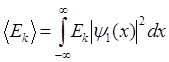

С помощью волновых функций можно найти среднее значение любой величины (если ее можно в принципе измерить экспериментально). Величина |ψ(x)|²dx - вероятность нахождения частицы в интервале dx. В случае многократных наблюдений за частицей |ψ(x)|²dx - доля частиц, которые находились в этом интервале, т.е. |ψ(x)|² является функцией распределения по координате.

Найдем среднее значение потенциальной энергии гармонического осциллятора

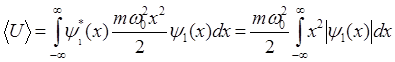
С учетом явного вида волновой функции 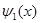получаем

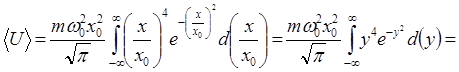
Где 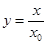. Поскольку функция, стоящая под знаком интеграла, является четной, то

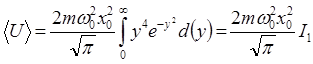
где интеграл 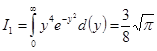. Таким образом, среднее значение потенциальной энергии гармонического осциллятора в первом возбужденном состоянии равно

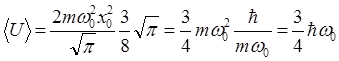
Найдем теперь среднее значение кинетической энергии

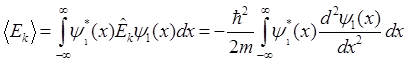
Вторая производная волновой функции 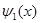по координате x равна

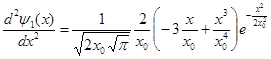
Подставляя 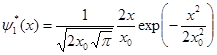и 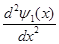в выражение для 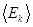, получаем

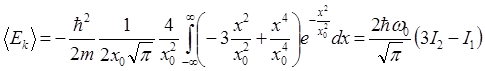
где интеграл 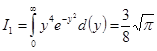и 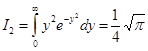. Подставляя I₁ и I₂ в выражение для 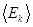, получаем

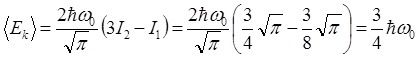
Таким образом, мы показали, что для первого возбужденного состояния гармонического осциллятора средние значения потенциальной энергии <U> и кинетической <E_k> энергии равны между собой и составляют половину полной энергии осциллятора 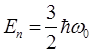. Можно показать, что это утверждение будет справедливым и для любого другого состояния квантового гармонического осциллятора. Полученный результат подтверждает, что в квантовой механике равенство полной энергии частицы сумме ее потенциальной и кинетической энергий выполняется только для средних значений энергии.

Задача 3. Частица массы m движется в трехмерном потенциальном поле

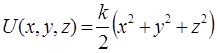
где k- постоянная (трехмерный гармонический осциллятор). Найдите собственные значения энергии частицы и кратность вырождения n-го энергетического уровня.

Решение: Поскольку движение частицы вдоль осей x,y и z происходит независимо, то будем искать волновую функцию в виде произведения

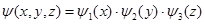
где 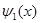зависит только от координаты x, 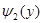- только от y и 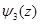- только от z. Подставляя 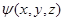в уравнение Шредингера 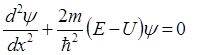, получаем

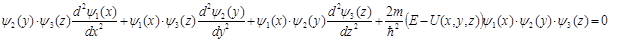
Разделив это уравнение на 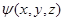и используя данный в условии задачи вид зависимости U(x,y,z), приходим к соотношению

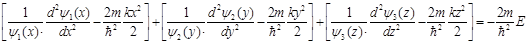
Первое выражение в квадратных скобках в левой части этого равенства является функцией только координаты 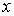, второе выражение в квадратных скобках является функцией только координаты 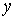, третье - функцией только координаты 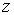. Поскольку их сумма равна постоянной величине, то каждое из этих слагаемых также должно равняться постоянной величине

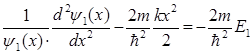
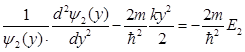
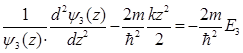
где константы E₁, E₂, E₃ имеют размерность энергии, и удовлетворяют условию E₁+E₂+E₃=E. Таким образом, получаем три уравнения для одномерного гармонического осциллятора, решения которых нам уже известны 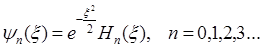и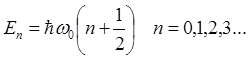

Волновая функция трехмерного гармонического осциллятора представляет собой произведение трех волновых функций для одномерного гармонического осциллятора 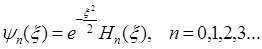и зависит от трех квантовых чисел n₁, n₂ и n₃

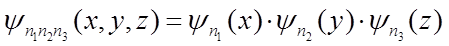
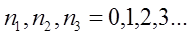
Для энергии трехмерного гармонического осциллятора получаем следующее выражение

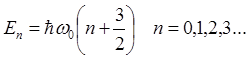где n=n₁₊ n₂₊n₃

Найдем кратность вырождения n- го энергетического уровня трехмерного гармонического осциллятора. Для заданного значения n кратность вырождения уровня равна числу возможных перестановок трех чисел n₁, n₂ и n₃, сумма которых равна n. Найдем сначала число перестановок при фиксированном значении n₁. Оно, как легко видеть, равно числу возможных значений (или, что то же самое, n₃). Число n₂ при заданном n₁ может меняться в пределах от 0 до (n- n₁), т.е. принимает (n- n₁+1) значение. Следовательно, число перестановок при фиксированном n₁ равно (n- n₁+1). Суммируя это выражение по n₁, находим кратность вырождения n-го уровня K_n

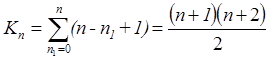
Основное состояние трехмерного гармонического осциллятора (n=0) оказывается невырожденным, K₀=1. Первое возбужденное состояние (n=1) имеет кратность вырождения K₁=3, ему соответствуют тройки квантовых чисел (100), (010), (001).

8. Спектр колебаний двухатомного линейного кристалла из химически одинаковых атомов.

9. Свойства колебаний решетки на примере моноатомного линейного кристалла, если один из атомов заменен на более легкий атом

10. Задачи по теме кристаллическая решетка

Примеры задач.

Задача 1. Расстояние d между атомными плоскостями в кристалле поваренной соли равно 0.281 нм. При каком максимальном угле падения будет наблюдаться усиление отраженных рентгеновских лучей с длиной волны l=0.1 нм при первом порядке отражения?

Задача 2. Пусть а –длина ребра основания куба в ГЦК решетке. Каково расстояние между ближайшими соседними атомами в ГЦК решетке?

Задача 3. Пусть а –длина ребра основания куба в ОЦК решетке. Каково расстояние между ближайшими соседними атомами в ОЦК решетке?

Задача 4. Вычислить относительное изменение объема кристалла при переходе железа от ГЦК к ОЦК решетке, если межатомные расстояния в этих структурах соответственно 0.254 и 0.248 нм

11. Задачи по теме «Электроны в твердом теле»

Примеры задач.

Задача 1. Вычислить энергию Ферми, отсчитанную от дна зоны проводимости, при температуре 0К для валентных электронов натрия. Оценить максимальную скорость электронов при этой температуре. Плотность натрия r=0.97 ×10³ кг/м³

Задача 2. Определить величину химического потенциала в германии при температуре 300К, если ширина запрещенной зоны 0,75эВ. Эффективная масса электронов 0.56 массы свободного электрона, а эффективная масса дырки 0.59 массы свободного электрона.

Задача 3. Вычислить энергию Ферми, отсчитанную от дна зоны проводимости, при температуре 20К для кристалла германия, содержащего 10²³ м^-3 атомов мышьяка и 5×10²² м^-3 атомов галлия.

Задача 4. Удельное сопротивление собственного германия при комнатной температуре 47 Ом×см, подвижность электронов 3900 см²/(В×с), подвижность дырок 1900 см²/(В×с). Найти концентрацию собственных носителей заряда. Какую нужно ввести концентрацию доноров, чтобы удельное сопротивление полупроводника снизилась до 20 Ом×см.

Задача 5. Найти скорость звука в алмазе используя модель Дебая.

12. Упругие свойства твердых тел.

Примеры задач.

Задача 1. Прямоугольный изотропный брусок размером 8´3´2 см³ поместили в жидкость под гидростатическим давлением 1000 Н/см². При этом объем уменьшился на 1 мм³. Найти компоненты тензора напряжений и деформаций.

13. Магнитные свойства твердых тел

Примеры задач.

Задача 1

Найти квазиклассические уровни энергии для частицы с квадратичным законом дисперсии в магнитном поле произвольного направления.

Решение.

Поскольку мы рассмотрим точку k= k₀ в k-пространстве, в которой энергия электрона 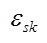имеет экстремум, то в её окрестности ф-ция 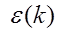может быть разложена в ряд Тейлора по степеням разности q=k-k₀. Поскольку это вблизи точки экстремума, то первая производная по q будет =0, так что первые члены такого разложения квадратичны.

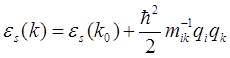, где

Приведем тензор m_ik к диагональному виду и будем отсчитывать энергию и импульс от точки экстремума (для определенности минимума).

Тогда

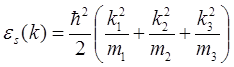(1)

где m₁, m₂, m₃ - главные значения тензора m_ik (положительные величины). Обозначив через n единичный вектор в направлении поля Н, имеем

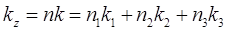(2)

n₁, n₂, n₃ -направляющие косинусы поля относительно главных осей тензора m_ik Нам надо найти площадь S той части плоскости (2), которая лежит внутри эллипсоида (1); она может быть представлена в виде интеграла

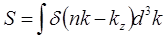
взятого по объему эллипсоида (1).

Эта формула берется из след рассуждений: пусть f(x,y,z)=const семейство пов-стей, заполняющих некоторый объем. Расстояние dl между 2-мя бесконечно близкими пов-стями семейства: dl=df/|Ñf|, а объем между этими пов-стями dV=S(f)dl, где S(f) площадь пов-сти с заданным значением f.

dV=S(f) df/|Ñf|

Умножив равенство dV|Ñf|=S(f) df на d-функцию d(f) и проинтегрировав по объему и по df получим площадь пов-сти f(x,y,z)=0 в виде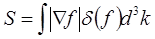

В нашем случае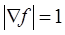

Заменой переменных 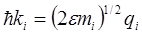интеграл приводится к виду

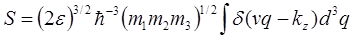
где вектор v в q-пространстве имеет компоненты 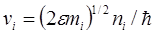, а интегрирование производится по объему сферы q²=1 Интегрирование легко выполняется в цилиндрических координатах с осью вдоль v и дает

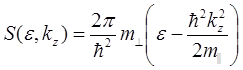
где

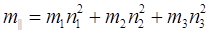
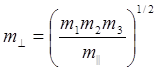
Подставив в выражение для площади сечения

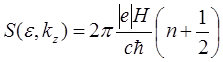
изоэнергетической поверхности плоскостью k_z=const, найдем уровни энергии

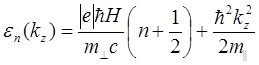
Задача 2 Рассчитать относительную разность заселенностей электронами либо протонами 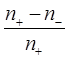двух энергетических уровней при температуре 100 К, возникших в результате взаимодействия магнитного момента электрона либо протона с постоянным магнитным полем, индукция которого 1 Тл. Здесь 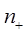и 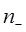число электронов (протонов), имеющих положительную либо отрицательную проекцию магнитного момента на направление индукции магнитного поля соответственно. Фактор спектроскопического расщепления для электрона g_e=2, а для протона g_p=5.58

14. Оптические свойства твердых тел.

Дата добавления: 2014-10-15