Характеристика дерев

Лекція 4

BIBLIOGRAFIA

1. Ș. Traușan Matu, Programare în LISP: Inteligența artificială și Web semantic, Ed. Polirom, Iași, 2004, 288 p.

2. Cristea D., Ioniţă M., Pistol I. C., Inteligenţã Artificială, Ed. UAIC, Iaşi, 192 p. –

http://thor.info.uaic.ro/~dcristea/cursuri/IA/carteaIA.pdf

Тема: "Характеристика дерев. Остови графу. Задача про мінімальне з’єднання."

Дисципліна: "Дискретна математика"

Викладач: Гусарова І. Г.

Харків,2014

Мета лекції: розглянути означення, характеристики, властивості дерев та остовів графа; також розглянути задачу про мінімальне з’єднання.

Зміст:

1. Характеристика дерев.

2. Позначені дерева.

3. Остови графа.

4. Алгоритм пошуку у глибину.

5. Задача про мінімальне з’єднання.

Базові Поняття та Ключові Слова:

1. Дерево.

2. Позначене дерево.

3. Остовний підграф.

4. Матриця Кірхгофа.

5. Економічне дерево.

Приведемо ряд ознак, що дозволяють розпізнати в даному графі дерево.

Теорема 1. Нехай граф з вершинами, де ; наступні його властивості еквівалентні й визначають як дерево:

1) – зв'язний і не містить циклів;

2) – зв'язний і його цикломатичне число ;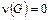

3) – не містить циклів і має ребро;

4) – зв'язний і має ребро;

5) не містить циклів, але додавання ребра між двома будь-якими вершинами приводить до появи одного (і тільки одного) циклу;

6) зв'язний, але втрачає цю властивість після видалення будь-якого ребра;

7) усяка пара вершин з'єднана ланцюгом, і тільки однієї.

Доведення. Покажемо, що кожна наступна властивість випливає з попереднього, а властивість 1 випливає із властивості 7. Нехай – кількість ребер, – число компонентів зв’язності.

1) 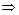2) у силу наслідку 1.

2) 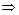3): якщо , то .

3) 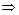4): якщо 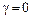й , то .

4) 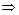5): якщо й , то 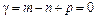, тобто не містить циклів. Якщо ж додати ребро, то одержимо , і з'являється один і тільки один цикл.

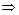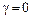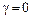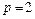5) 6): якбине був зв'язний, то в ньому були б дві вершини й , не з'єднані ніяким ланцюгом. У такому випадку приєднання ребра не приводить до появи циклу, що суперечить 5). Виходить, зв'язний, . Крім того , отже, , тобто . Якщо ж видалити будь-яке ребро, то й залишається ; тому , звідки й стає незв'язним.

6) 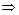7): тому що зв'язно, то будь-які дві вершини з'єднані ланцюгом. Такий ланцюг може бути тільки одна, інакше видалення ребра, що належить другого ланцюга й не приналежного першої, не порушило б зв’язності.

7) 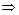1): якщо граф має цикл, то в ньому існує хоча б одна пара вершин, з'єднаних двома ланцюгами.

Дата добавления: 2014-10-15