Остови графа

Визначення. Остовом або каркасом графа 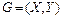називається підграф 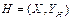без циклів, що містить всі вершини 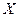і максимально велике число ребер.

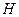Якщо – зв’язний, то остов є дерево, якщо містить 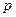компонент зв’язності, то остов (каркас) 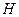складається з 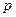дерев.

Два остови у вважаються різними, якщо вони відрізняються хоча б одним ребром, тобто як графи. Для того щоб мав більше одного остова, необхідно і достатньо існування хоча б одного циклу в .

Задача визначення числа всіх остовів графа і їх фактичного конструювання є важливою для застосувань. Зрозуміло, її достатньо розв’язати для зв’язного . Для повного графа без петель та кратних ребер перелічення остовів є перелічення всіх позначених дерев з 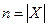вершинами, так що число остовів дорівнює 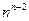. У загальному випадку число остовів одержав Кірхгоф у 1847 р.

Визначення. Матрицею Кірхго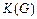фа графа без петель та кратних ребер називається 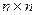– матриця з елементами

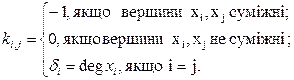
Сума елементів у кожному рядку (і кожному стовпці) матриці 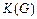дорівнює нулю. У будь-якої квадратичної матриці з такою властивістю рядків і стовпців, а не тільки у матриці Кірхгофа 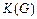, алгебраїчні доповнення 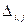всіх елементів 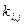рівні між собою: .

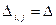У матриці ж 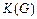величина 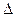дорівнює числу остовних дерев.

Теорема 3. (Кірхгоф) Число остовних дерев у зв’язному графі без петель та кратних ребер з 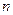вершинами(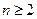) дорівнює алгебраїчному доповненню будь-якого елемента матриці Кіргхгофа .

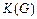Наслідок. Справедлива формула Келі для числа позначених дерев з 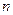вершинами .

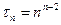Доведення. Всі позначені дерева з 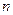вершинами утворюють в точності множину остовних дерев повного графа 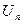. За теоремою 3 їх число дорівнює алгебраїчному доповненню 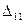елемента 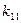матриці Кірхгофа

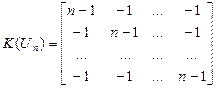
розміру .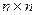

Визначник порядку 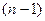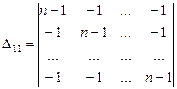зручно перетворити, замінивши спочатку перший рядок сумою всіх рядків, а потім, додаючи одержаний рядок з одиниць до рядків з номерами .

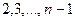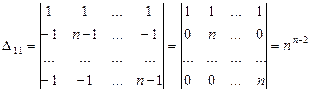
Дата добавления: 2014-10-15