Обработка результатов измерений

Измерение любых физических и химических величин из-за несовершенства измерительных приборов и наших органов чувств всегда связаны с погрешностями. Погрешности измерений разделяются на систематические и случайные.

Систематические погрешности обусловлены причинами, действующими вполне определенным образом (например, неправильной градуировкой или установкой измерительных приборов, изменением внешней температуры, давления и т. д.). Эти погрешности могут быть всегда устранены или достаточно точно учтены путём тщательной проверки аппаратуры перед измерениями и введением соответствующих поправок при обработке экспериментальных результатов.

Но часто систематические погрешности не исключают из результата измерения, а рассчитывают, отдельно их указывая. В качестве границ неисключённой систематической погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений. В общем случае (при равномерном распределении) неисключаемые систематические погрешности вычисляют по формуле

,

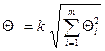где 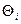- граница i-ой неисключённой систематической погрешности; k – коэффициент, определяемой доверительной вероятностью. k = 1.1 при P = 0.95 и k = 1.4 при P = 0.99.

Случайные погрешности обусловлены большим числом отдельных причин, не поддающихся точному учёту и действующих в каждом отдельном опыте различным образом. Случайные ошибки во всех случаях не могут быть исключены из результата измерения. Величину случайных погрешностей определяют принципиальная схема эксперимента, отклонение реальных условий опыта от заданных и, в значительной мере, субъективные особенности экспериментатора. Случайные погрешности подчиняются законам вероятности, в связи с чем многократное повторение одного и того же измерения уменьшает их влияние.

Доверительные границы (без учёта знака) случайной погрешности результата измерения рассчитывают [12] по формуле:

,

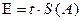где t - коэффициент Стьюдента, который в зависимости от доверительной вероятности P и числа результатов наблюдений n находят по таблице (например, при P = 0.95 если n = 5, то t = 2.571; если n = 16, то t = 2.120; если n = 30, то t = 2.042; при большем числе n, чем 30, независимо от самого числа n коэффициент t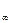= 1.960); величина S (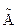) называется среднеквадратичным отклонением результата измерения и определяется по формуле

,

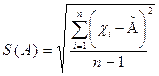где - i-ый результат наблюдения; - результат измерения (или среднеарифметическое результатов наблюдений); n - число результатов измерений. Следует иметь в виду, что пользоваться этой формулой можно только в случае нормального распределения результатов наблюдений.

Точность измерения характеризуется отклонением среднего значения серии измерений от истинной величины аналитического сигнала. Нетрудно заметить, что это отклонение определяется систематической и случайной погрешностями измерения.

При статистической обработке группы результатов наблюдений выполняют следующие операции:

1) Исключают известные систематические погрешности из результатов наблюдений (если они известны).

2) Устанавливают и исключают грубые погрешности (промахи) из результатов наблюдений. В случае нормального распределения результатов наблюдений промахи исключают в соответствии с требованиями стандарта [13]. Для этого подсчитывают среднеарифметическое результатов наблюдений:

,

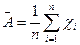и стандартное отклонение для него по формуле (3).

Чтобы оценить принадлежность 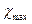и 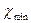к данной нормальной совокупности и принять решение об исключении или оставлении этих значений в группе результатов наблюдений, находят отношения:

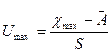и

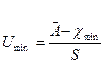
Результаты этих отношений сравнивают с величиной β, взятой из таблицы для данного объема выборки n и принятого уровня значимости α = 1- P, где Р – доверительная вероятность.

Есл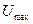и и 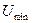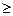β, то подозреваемый в анормальности результат наблюдения должен быть исключен из группы. В противном случае он остаётся в группе.

3) Если были установлены промахи, их исключают из группы результатов наблюдений и снова подсчитывают среднеарифметическое выборки, принимая его за результат измерения ().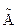

4) Вычисляют оценку среднеквадратичного отклонения результата измерения: (уже без промахов) по формуле

.

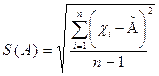5) Проверяют гипотезу о том, что результаты наблюдений принадлежат нормальному распределению.

При числе результатов наблюдений n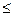15 проверки не производят, но дальнейшие операции с группой результатов наблюдений проводят по стандарту [12], если заранее известно, что результаты наблюдений принадлежат нормальному распределению.

При числе результатов наблюдений 50>n>15 проверку принадлежности их к нормальному распределению производят с помощью составного критерия.

И при n>50 нормальность распределения оценивается по стандарту [14] с помощью критериев 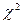Пирсона или 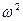Мизеса-Смирнова.

6) Вычисляют доверительные границы случайной погрешности результата измерения (по известной формуле ε .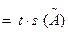

7) Вычисляют границы неисключённой систематической погрешности результата измерения по известной формуле

.

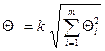8) Вычисляют доверительные границы общей погрешности результата измерения (Δ).

При этом если отношение 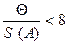, то систематическими погрешностями пренебрегают, и границы общей погрешности принимают Δ = ε.

Если 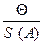> 8, то пренебрегают случайными погрешностями и .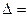

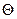Если 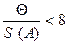, но > 0,8, то граница общей погрешности результата измерения определяется по формуле

Δ = 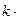S_Σ,

где 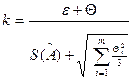- коэффициент, зависящий от соотношения случайной и систематической погрешностей, а S _Σ = 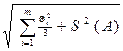- оценка суммарного среднеквадратичного отклонения результата измерения.

Представляют результаты измерений по стандарту [15].

При симметричной доверительной погрешности результаты измерений представляют по форме: 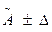, P. При этом числовое значение результата измерений должно оканчиваться цифрой того же разряда, что и значение погрешности Δ.

При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей, результаты измерений представляют в форме 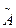, 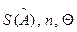и Р.

Оценк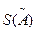и и при обработке результатов измерений могут выражаться в абсолютной и относительной формах.

При испытаниях в технике (особенно в разрушающих методах измерений) систематической погрешностью часто пренебрегают, и результат измерений представляют в виде: 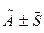, коэффициент вариаци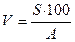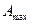и %, и 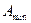. Доверительная вероятность принимается часто равной P = 0.95 или P = 0.9.

Пример: Взят из стандарта [16].

Проведено 10 наблюдений (n = 10) при сличении рабочего эталона единицы длины – штрихового метра с первичным эталоном интерференционным методом. Полученные величины, превышающие 1м в мкм (A_i): 1.47 – 1.324 – 1.418 – 1.363 – 1.598 – 1.647 – 1.485 – 1.306 – 1.463 – 1.625.

1. Результат измерений: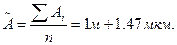

2. Среднеквадратичное отклонение результата измерений: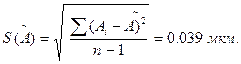

3. Установленные по паспорту прибора неисключённые систематические погрешности:

- из-за неточного определения показателя преломления воздуха -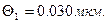

- из-за неточного значения длин волн -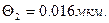

- из-за неточного значения температуры -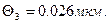

- из-за неточного определения поправок на размер коллиматорной щели -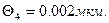

Требуется определить доверительные границы погрешности рабочего эталона.

Решение:

1. Определяют границы неисключённой систематической погрешности (при P=0.99).

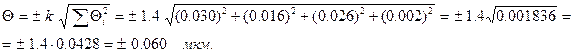
2. Вычисляют среднеквадратичное отклонение суммы неисключённых систематических и случайных погрешностей:

S _Σ =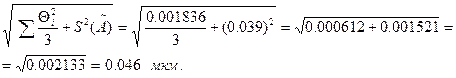

3. Вычисляют доверительные границы случайных погрешностей: ε = 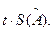Из таблиц коэффициента Стьюдента при P = 0.99, n = 10 t = 3.25.

ε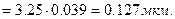

4. Определяют коэффициент

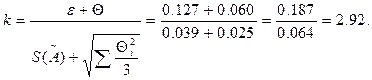
5. Доверительные границы суммарной погрешности:

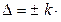S _Σ =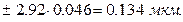

Форма представления результата:

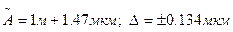при P = 0.99.

Дата добавления: 2014-10-15