Перетворення прямокутних координат

Всі прямокутні системи координат в досліджуваному просторі рівноправні. Ті чи інші переваги віддають виходячи з особливостей конкретної задачи. Використання різних систем координат ставить завдання перетворення координат точки, тобто задачу обчислення її координат в одній системі координат за її координатами в іншій системі.
Нехай 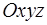деяка прямокутна система координат в просторі, яку ми умовно назвемо старою, а 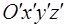- друга прямокутна система координат, яку будемо називати новою (рис. 4.1). Вважаємо, що відомі координати точки і векторів:

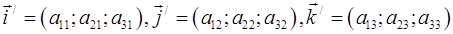
в старій системі координат. Нехай для точки М відомі її координати у старій і координати в нової системах координат. Це означає, що виконуються дві рівності: 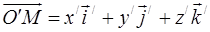т

.

Рис 6.1

Вектори та пов'язані співвідношенням 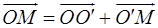, причому координати вектора 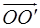є також координатами початку О' нової системи координат відносно старої, тобто:
.

Тому

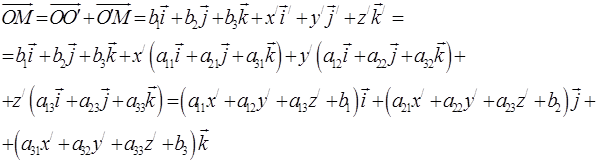
тобто отримано розкладання вектора в репері старої системи координат. Прирівнюючи відповідні коефіцієнти розкладань в старому і в новому базисах, отримуємо

(6.1)

Це співвідношення виражає старі координати через нові і, по суті, є системою трьох лінійних рівнянь відносно невідомих . Щоб знайти нові координати по відомим старим, необхідно вирішити цю систему відносно нових координат. Система при будь-яких 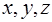має єдиний розв’язок, оскільки її визначник відмінний від нуля. Це випливає з того, що виконані рівності:

оскільки вектори утворюють правий ортонормований базис і об’єм побудованого на них паралелепіпеда дорівнює 1 (або -1 у випадку лівого базису).
Набір коефіцієнтів в системі (4.1) відображає положення репера нової системи координат, а вільні члени 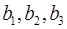характеризують зміну початку координат. Якщо репер системи координат не змінився, а змінився лише початок координат, то формули перетворення мають вигляд:

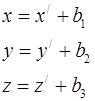
Це перетворення називають паралельним перенесенням системи координат в просторі на вектор .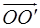
Прямокутна система координат на площині відрізняється від просторової лише тим, що репер складається з двох векторів, а точки мають лише дві координати. Перетворення системи координат на площині описується рівняннями

(6.2)

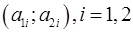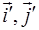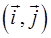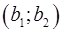де , - координати векторів нового репера відносно старого , а - координати точки О' початку нової системи координат в старій системі координат.
Перетворення паралельного перенесення системи координат на площині виглядає так:

Якщо початок нової і старої систем координат на площині збігаються, а змінюється лише репер системи координат, то формули перетворення координат мають вигляд:
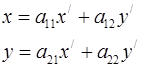(6.3)

Рис. 6.2.

Тут можливі два випадки. У першому з них новий репер може бути отриманий з старого поворотом останнього на деякий кут (рис. 6.2) навколо загального початку систем координат, причому вважають, що при повороті проти напрямку (за напрямком) годинникової стрілки. У цьому випадку перетворення (6.3) називається поворотом системи координат на площині на кут 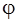. Координати векторів та нового репера відносно старого виражаються через кут повороту :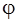

(рис. 6.2)

Знаючи координати векторів нового репера відносно старого, ми можемо записати рівняння для повороту системи координат на площині:
(6.4)
Якщо перетворення полягає в послідовному виконанні повороту і паралельного перенесення, то воно має вигляд:
(6.5)
Система (6.4) легко вирішується відносно , і зворотне перетворення координат, що відображає перехід від нової системи координат до старої, буде мати вигляд:
,
де .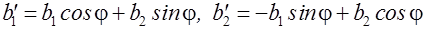

Стара система координат виходить з нової за допомогою повороту на той самий кут 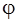, але в протилежну сторону (на кут - 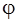в позитивному напрямку), і паралельного переносу (на вектор ).
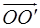У другому випадку за допомогою повороту старого репера навколо початку координат на деякий кут 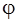можна поєднати лише вектори 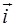та ,але при цьому вектори та виявляться протилежними і для їх поєднання буде потрібно виконання перетворення дзеркального відображення площини відносно першої осі координат.

У першому випадку про два репери на площині кажуть, що вони мають однакову орієнтацію, а в другому - протилежну. Аналогічну термінологію використовують і для простору. Якщо початок нової і старої прямокутних систем координат в просторі співпадають і змінюється лише репер системи координат, то формули перетворення координат мають вигляд:
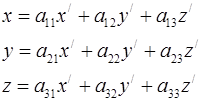(6.6)
Перетворення (6.6) називають поворотом системи координат в просторі, якщо репери нової і старої систем координат мають однакову орієнтацію, тобто є обидва правими або лівими.

Дата добавления: 2014-10-15