
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Полярна система координат
|
|
|
|
Крім прямокутної системи координат на площині часто використовують полярну систему координат. Виберемо в площині довільну точку О, назвемо її полюсом і проведемо промінь Ор, який називається полярною віссю, задамо масштабну одиницю довжини т = |ОЕ|. Положення будь-якої точки М у площині визначимо так: сполучимо відрізком прямої полюс з точкою М. Довжину відрізка ОМ позначимо через 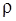 . Цей відрізок називається полярним радіусом точки М; задамо на ньому напрям від О до М. Дістанемо вісь ОМ. Таким чином, маємо дві осі: перша — полярна вісь, а друга — вісь ОМ. Величину кута рОМ (з урахуванням напряму повороту) позначимо через
. Цей відрізок називається полярним радіусом точки М; задамо на ньому напрям від О до М. Дістанемо вісь ОМ. Таким чином, маємо дві осі: перша — полярна вісь, а друга — вісь ОМ. Величину кута рОМ (з урахуванням напряму повороту) позначимо через 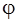 (у градусах, радіанах або абстрактних одиницях) і назвемо його полярним кутом точки М (рис. 6.3).
(у градусах, радіанах або абстрактних одиницях) і назвемо його полярним кутом точки М (рис. 6.3).
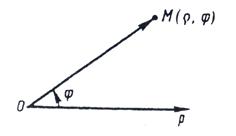
Рис. 6.3.
Полярними координатами точки М називається упорядкована пара чисел (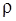 ,
,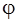 ), де
), де 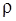 — довжина полярного радіуса;
— довжина полярного радіуса; 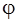 — величина полярного кута точки М. Для полюса
— величина полярного кута точки М. Для полюса 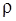 = 0, а
= 0, а 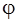 має довільне значення. Той факт, що числа
має довільне значення. Той факт, що числа 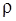 і
і 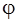 —координати точки М, записують так: М (
—координати точки М, записують так: М (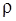 ,
,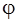 ). Полярні координати
). Полярні координати 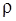 і
і 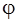 однозначно визначають положення точки на площині. Обернене твердження неправильне, оскільки кожній точці координатної площини відповідає одне й те саме
однозначно визначають положення точки на площині. Обернене твердження неправильне, оскільки кожній точці координатної площини відповідає одне й те саме 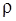 і нескінченна множина полярніх кутів, які можуть відрізнятись один від одного на 2
і нескінченна множина полярніх кутів, які можуть відрізнятись один від одного на 2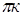 , де к є Z.
, де к є Z.
Для того щоб дістати взаємно однозначну відповідність, на полярний кут 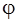 накладають обмеження: 0
накладають обмеження: 0
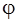 < 2
< 2 або
або  <
< 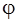 <
<  . Ці значення називаються головними значеннями полярного кута. Знайдемо залежність між полярними і прямокутними декартовими координатами точки М. Сумістимо прямокутну систему координат
. Ці значення називаються головними значеннями полярного кута. Знайдемо залежність між полярними і прямокутними декартовими координатами точки М. Сумістимо прямокутну систему координат  з полярною так, щоб початок координат збігався з полюсом, а полярна вісь — з додатною
з полярною так, щоб початок координат збігався з полюсом, а полярна вісь — з додатною
піввіссю абсцис (рис.6.4).
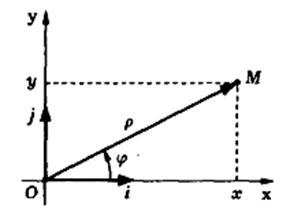
Рис. 6.4.
Прямокутні координати (х; у) точки М на площині виражаються через її полярні координати 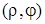 за допомогою співвідношень
за допомогою співвідношень

З урахуванням обмеження 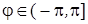 на полярний кут полярні координати точки визначаються через її прямокутні координати наступним чином:
на полярний кут полярні координати точки визначаються через її прямокутні координати наступним чином:
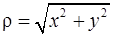 ;
;

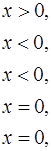

Приклад 6.1. Знайти полярні координати точок М (3, 4) та N (-1; 1).
Розв’язання. Для точки М маємо:  а для точки N -
а для точки N -  .
.
Відповідь:  .
.
6.3. Циліндрична і сферична системи координат
Якщо в прямокутній системі координат 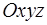 замість перших двох координат х і у взяти полярні координати, а третю залишити без змін, то дістанемо циліндричну систему координат. Координати точки Р простору в цій системі записуються у вигляді Р (
замість перших двох координат х і у взяти полярні координати, а третю залишити без змін, то дістанемо циліндричну систему координат. Координати точки Р простору в цій системі записуються у вигляді Р ( ,
, , z).
, z).
Знайдемо залежності між прямокутними декартовими координатами точки Р (х, у,z) і її циліндричними координатами Р ( ,
, , z). (рис. 6.5). Враховуючи формули полярної системи координат, маємо
, z). (рис. 6.5). Враховуючи формули полярної системи координат, маємо
 , де 0
, де 0 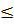
 < +
< +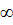 ; 0
; 0 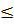
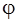 < 2
< 2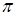 ;
;  z < +
z < +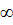 .
.

Рис. 6.5.
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 1377; Нарушение авторских прав?; Мы поможем в написании вашей работы!