Пример. Минимальной ДНФ (МДНФ) булевой функции называется одна из её тупиковых ДНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты)

Определение.

Минимальной ДНФ (МДНФ) булевой функции называется одна из её тупиковых ДНФ, которой соответствует наименьшее значение критерия минимизации (индекса простоты) ДНФ.

Пусть имеется функция 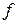, заданная в виде СДНФ:

.

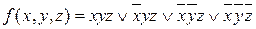Выполним операции полного склеивания следующим образом:

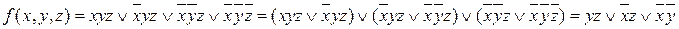
Операцию склеивания можно выполнить другим способом:

.

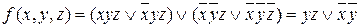В обоих случаях получены тупиковые ДНФ функции 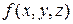. Вторая тупиковая ДКФ проще первой, поскольку содержит меньшее количество символов переменных и знаков операций.

Для анализа различных представлений булевой функции через КНФ и получения минимальных КНФ (МКНФ) необходимо использовать принцип двойственности. Двойственные понятия соответственно называются терминами: имплицента, простая имплицента, полная система имплицент, сокращенная КНФ, тупиковая КНФ, минимальная КНФ.

Проблема синтеза логических схем в булевом базисе связана с задачей минимизации булевых функций, которая в общем случае имеет две постановки:

- в аналитической форме;

- в геометрической форме (задача о покрытии).

Употребляются два языка: аналитический и геометрический.

Для решения данной задачи в современной теории и практике алгебры логики существуют следующие основные подходы:

- перебор (просмотр) всех возможных ДНФ и КНФ произвольной функции с целью поиска минимальной формы (первый подход);

- упрощение конкретной функции, достигаемое путем различных тождественных преобразований, с целью получения формулы, эквивалентной исходной, но реализуемой проще (второй подход).

Процесс перебора всех возможных ДНФ и КНФ функции является, хотя и наиболее понятным, но достаточно трудоемким процессом. Им нельзя воспользоваться практически уже с 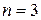, а для 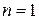и 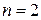проблема является тривиальной.

Процесс поиска минимальных форм становится более наглядным и целеустремленным, если использовать второй подход, т.е. некоторые аналитические и графические представления и специально разработанную для этой цели символику.

В общем случае минимальные формы булевых функций аналитически получают в такой последовательности:

- получают и анализируют конкретную функцию алгебры логики, определенную для всевозможных наборов значений аргументов;

- полученную функцию представляют через основные операции в любой из двух совершенных нормальных форм (СДНФ или СКНФ);

- находят сокращенную ДНФ (КНФ) (любая функция имеет одну такую форму);

- находят возможные тупиковые ДНФ (КНФ);

- из полученных тупиковых форм выбирают минимальные ДНФ (КНФ).

Для нахождения упрощенного аналитического выражения используются следующие очевидные преобразования формул булевой алгебры, которые традиционно называются «операциями».

Рассмотрим данные операции, принимая следующие обозначения: 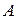- некоторая элементарная конъюнкция переменных; 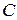- некоторая элементарная дизъюнкция переменных; 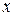- булева переменная.

Операция неполного дизъюнктивного склеивания:

.

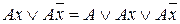Операция дизъюнктивного поглощения:

.

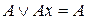Выполнение двух указанных операций последовательно представляет собой выполнение операции полного дизъюнктивного склеивания:

.

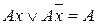Операция неполного конъюнктивного склеивания:

.

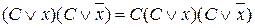Операция конъюнктивного поглощения:

.

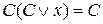Операция полного конъюнктивного склеивания:

.

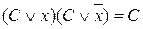Существует несколько известных аналитических и геометрических методов получения минимальных ДНФ (КНФ): метод Квайна−Мак-Класки, метод Порецкого-Блейка, метод минимизирующих карт (диаграммы Карно-Вейча), метод многомерных кубов и др.

Метод минимизирующих карт (диаграммы Карно-Вейча)

Целью минимизации является нахождение минимальной из тупиковых ДНФ (КНФ), т.е. нахождение минимального покрытия данной функции. Для этого необходимо построить все возможные тупиковые ДНФ (КНФ), используя операции склеивания и поглощения для данной функции. Методика использования минимизирующих карт (методика диаграмм Карно и Вейча) позволяет выполнить указанные операции графически. Диаграммы Карно-Вейча представляют собой развертки кубов на плоскости.

Карты Карно (диаграммы Вейча) представляют собой специально организованные таблицы соответствия (истинности). Значения не более двух переменных располагаются в заголовках строк и столбцов карты в таком порядке, что каждый последующий отличается от предыдущего значением только одной из переменных, например, (0, 0), (0, 1), (1, 1), (1, 0). Клетки, расположенные по краям таблицы, считаются соседними и обладают этим свойством.

Каждой конституенте соответствует одна ячейка таблицы. Нуль или единица в ячейке определяет значение функции на данной интерпретации.

При таком расположении минтермы (макстермы), к которым применима операция склеивания, располагаются в соседних ячейках карты, и склеивание производится графически посредством объединения ячеек в группы.

Дата добавления: 2014-10-22