
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример. Построить минимальную КНФ функции, заданной картой Карно (диаграммой Вейча), представленной в таблице 3.25
|
|
|
|
Построить минимальную КНФ функции, заданной картой Карно (диаграммой Вейча), представленной в таблице 3.25.
Таблица 3.25 − Карта Карно (диаграмма Вейча) для функции 
 

| ||||
Для получения МКНФ необходимо рассмотреть «нулевые» ячейки, максимизируя размеры их групп и минимизируя количество таких групп, и провести операцию склеивания (рис. 3.3).

Рисунок 3.3 − Карта Карно (диаграмма Вейча) для булевой функции 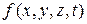
Запишем минимальную КНФ, объединив знаками конъюнкции элементарные дизъюнкции:  .
.
Минимизация частично определенных функций с использованием карт Карно. Для решения некоторых задач могут использоваться не все наборы входных данных, поэтому допустимо любое значение функции на неиспользуемых интерпретациях. Такая функция называется частично определенной. При минимизации такие функции доопределяются так, чтобы получить наиболее экономичную минимальную ДНФ (КНФ).
|
|
|
|
|
Дата добавления: 2014-10-22; Просмотров: 837; Нарушение авторских прав?; Мы поможем в написании вашей работы!