Определение. В алгебре логики из множества различных булевых функций переменных

Определение.

Типы булевых функций

В алгебре логики из множества 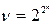различных булевых функций 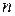переменных выделяются следующие пять типов булевых функций:

а) функции, сохраняющие константу 0;

б) функции, сохраняющие константу 1;

в) самодвойственные функции;

г) монотонные функции;

д) линейные функции.

Булева функция называется функцией, сохраняющей 0, если на нулевой наборе она равна 0, т.е. .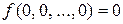

Так как на одном из 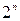наборов 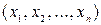значения таких функций фиксированы, то их число равно 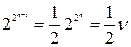, то есть половина всех функций 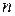переменных сохраняет константу 0.

Обозначим через 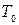класс функций, сохраняющих 0.

Булева функция называется функцией, сохраняющей 1, если на единичном наборе она равна 1, т.е. .

Их число, как и в предыдущем случае, равно половине общего числа всех функций 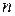переменных. Обозначим через класс функций, сохраняющих 1.

Дата добавления: 2014-10-22