Методы и критерии, используемых при построении доверительных интервалов

При моделировании экономических процессов наибольший интерес представляет возможность предсказания будущего развития процесса. Но, как известно, экономические процессы обычно являются стохастическими, поэтому указание их точечных значений лишено содержания, т.к. вероятность того, что прогнозируемый показатель в заданный момент времени будет равен значению, определяемому точечным прогнозом, практически равна нулю. Следовательно, в дополнение к точечному прогнозу необходимо дать возможные границы изменения прогнозируемого показателя – доверительные интервалы.

Доверительные интервалы учитывают неопределенность, связанную с ограниченным числом наблюдений, их возможностью отклонения от тренда, сохранением тенденции тренда.

Перед тем как перейти к оцениванию доверительных интервалов различных моделей, рассмотрим некоторые аспекты статистического оценивания параметров.

Имеются два важных типа параметрических оценок: точечные оценки и интервальные оценки. При точечном оценивании оценкой для истинного значения q₀ параметра q в 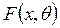служит наблюдаемая величина 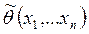, функция элементов выборки , распределение которой в некотором смысле концентрируется вокруг истинного значения q₀ параметра q. Дисперсия точечной оценки часто дает разумный критерий для измерения ее концентрации.

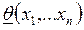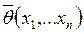При интервальном оценивании строятся две наблюдаемые случайные величины и , где 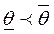, такие, что с заданной вероятностью случайный интервал 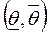содержит истинное значение q₀ и является в некотором смысле кратчайшим.

Интервальная оценка позволяет установить точность и надежность точечных оценок. Предположим, что найденная по некоторой выборке характеристика q* служит оценкой неизвестного параметра q. Ясно, что чем меньше абсолютная величина разности 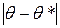, тем точнее q* определяет параметр q. Другими словами, если и 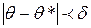, то чем меньше d, тем оценка точнее.

Однако статистические методы не позволяют категорически утверждать, что оценка q* удовлетворяет неравенству 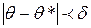, можно лишь говорить о вероятности, с которой это неравенство осуществляется.

Надежностью (доверительной вероятность) оценки q по q* называется вероятность р, с которой осуществляется неравенство .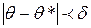

В статистической практике разработано два основных подхода к определению интервальных оценок. При байесовском подходе, основанном на теореме Байеса, рассматривается вероятностное распределение величины q р(q,х) и за меру правдоподобия интервала 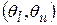принимается апостериорная вероятность того, что значение случайной величины q попадает в этот интервал.

Желательно было найти подход, который не требовал определения априорной вероятности оцениваемой величины. Проблема была пересмотрена с совершенно иных точек зрения Ю. Нейманом, исходя из идей Р. Фишера.

При предложенном подходе, основанном на понятии доверительного интервала, рассматриваются интервалы со случайными граничными точками, обладающие свойством, выраженном в терминах распределения 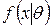: вероятность того, что интервал 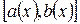содержит q равняется 1-a для заданного подходящим образом a.

Доверительным интервалом параметра q распределения случайной величины Х с уровнем доверия 100р%, порожденным выборкой 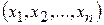, называется интервал с границам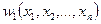и и 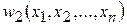, которые являются реализациями случайных величин 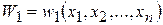и 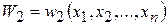, таких, что .

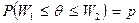Граничные точки доверительного интервала 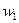и 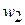называются доверительными пределами. Интерпретация доверительного интервала, основанная на интуиции, будет следующей, если р велико (скажем 0,95), то доверительный интервал почти наверняка содержит истинное значение q.

Теория доверительных интервалов для одного параметра достаточно развита. Определения и понятия интервального оценивания можно перенести на вектор q=(q₁,q₂,…,q_k) с заменой доверительного интервала доверительной областью в k -мерном пространстве. Доверительной областью вектора q генеральной совокупности является область, полностью определяемая результатами наблюдений, которая с близкой к единице доверительной вероятностью g=1-a содержит неизвестное значение вектора q. Очевидно, что существует бесконечное множество доверительных областей, соответствующих одному и тому же значению (1-a). Как правило, стараются определить доверительные области, имеющие минимальные размеры при данной вероятности (1-a).

Основную трудность в построении доверительной области представляет определение законов распределений подходящих статистик. В настоящее время эти вопросы достаточно хорошо разработаны только для нормального распределения наблюдаемых случайных величин.

В большинстве случаев, в том числе и при изучении экономических проблем, оказалось, что многомерное статистическое распределение является хорошим приближением к действительному распределению и статистические анализы, основанные на модели нормального распределения, вполне оправданы.

Для одномерного случая основой для выбора критерия или доверительного интервала является тот факт, что разность между средними значениями выборки и генеральной совокупности распределена нормально с известными математическим ожиданием и дисперсией. В математической статистике показано, что для независимых случайных величин х₁,...,х_n, распределенных по нормальному закону N(m, s²), величина 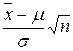имеет t-распределение c n-1 степенями свободы. Доверительный интервал определяется из формулы

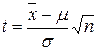. (8.1)

Условие, в силу которого значение t с вероятностью (1-a) попадет в соответствующий интервал запишется как:

,

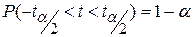где 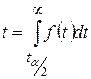. Заменив t на выражение из (8.1), получим:

.

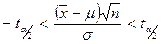Разрешив неравенство относительно m, вероятностное отношение перепишем в виде:

,

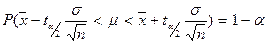то есть доверительным интервалом с вероятностью (1-a) для m будет:

.

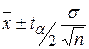Равенство (8.1) можно переписать в виде:

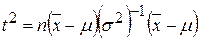. (8.2)

Полученное равенство обобщается на случай многомерной совокупности. Разработаны методы, позволяющие с помощью достаточно простых вычислений строить доверительные интервалы для многомерного распределения. Эти методы основаны на следующей теореме.

Теорема. Если m -мерный вектор T распределен N(0,T) (невырожденное распределение), то 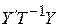имеет c² распределение с m степенями свободы.

Бозе Р. расширил данную теорему на случай совокупности N(m,S).

Рассмотрим k -мерное нормальное распределение N(m,å) с вектором средних m и ковариационной матрицей å. В многомерном случае используется тот факт, что разность между векторами среднего значения выборки и среднего значения генеральной сопокупности распределена нормально с вектором среднего значения и известной ковариационной матрицей. На случай k -мерной совокупности равенство (8.2) обобщается следующим образом:

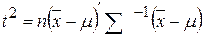. (8.3)

Статистика t² при k=1 имеет c² распределение с числом степеней свободы n=1. Статистика t² для любого k также имеет c² -распределение с числом степеней свободы n=k. Таким образом, с вероятностью a можно утверждать, что вектор m накрывается доверительной областью, задаваемой неравенством:

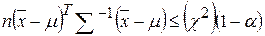, (8.4)

где å – ковариационная матрица, в случае если ковариационная матрица å не известна, используется ее несмещенная оценка . Доверительной областью в k -мерном пространстве будет эллипсоид (эллипс при k=2) с центром .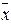

Хоттелинг ввел Т² - статистику, которая является многомерным аналогом квадрата величины t- распределения Стьюдента. Статистика Т² представляет собой просто геометрическое место точек эллипсоида доверительной области. Она выражается через объем выборки, выборочные средние и выборочную ковариационную матрицу:

,

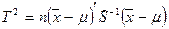Совокупность точек, координаты которых удовлетворяют неравенству:

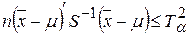
образуют в k -мерном пространстве внутренность и границу эллипсоида с центром в точке 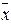, размеры и форма которого зависят от 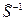и a.

Величину Т² можно связать с распределением F соотношением:

,

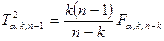где F_a имеет k и n-k степени свободы. Учитывая это, Т² можно записать следующим образом:

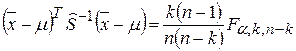. (8.5)

Как показано дальше, использование Т² - статистики Хоттелинга расширяет области построения совместных доверительных интервалов.

Дата добавления: 2014-10-22