
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическая модель операции обработки
|
|
|
|
Операция обработки представляет собой элементарный акт технологического процесса подготовки ЛА или его элемента, в результате которого меняется значение хотя бы одного из параметров этого аппарата. К абстрактной операции обработки относятся, в частности, технологические операции, связанные с изменением размеров элемента ЛА (членение), его положения в пространстве (транспортировка, повороты, подъемы) и сообщающие ему дополнительный признак (окраска, проверка) и т. д.
Комплекс технологического оборудования, обеспечивающий выполнение операции обработки, будем называть обрабатывающим агрегатом независимо от его реальной структуры и назначения. Построение математической модели операции обработки сводится к установлению соотношения между параметрами, характеризующими взаимодействие обрабатывающего агрегата и ЛА в процессе подготовки последнего к пуску.
Будем считать, что к моменту начала операции обработки tн известны значения всех параметров a1К обслуживаемого ЛА или его элемента, тогда значение параметров а2К для момента времени tК после операции будут определяться соотношениями вида
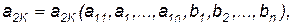 (4.2)
(4.2)
где К= 1, 2,...,n — количество параметров, характеризующих обслуживаемый ЛА или элемент; bi — некоторые параметры, характеризующие обрабатывающий агрегат; tK = tH + 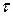 ,
, 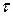 — длительность операции обработки.
— длительность операции обработки.
Поскольку параметры a1K и bi могут оказаться случайными, то и a2K представляет собой случайную величину. В связи с этим независимо от природы возникновения флуктуации обычно в этом случае пользуются соотношениями вида
 , (4.3)
, (4.3)
где δa2К — случайные отклонения величины а2К от некоторого неслучайного значения а2K0, заданные соответствующими законами распределения.
Кроме соотношений (4.2) и (4.3) операцию обработки описывают зависимости, определяющие режим функционирования обрабатывающего агрегата во времени. В том случае, когда отсутствует централизованное управление технологическими циклами во времени, операция может начинаться в любой момент времени при условии, что обрабатывающий агрегат готов к работе и к нему уже поступил очередной обслуживаемый ЛА или его элемент. Момент начала операции определяется как
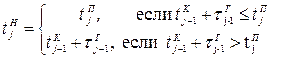 , (4.4)
, (4.4)
где tj — момент поступления j -го ЛА к обрабатывающему агрегату;
 Г — время, затрачиваемое на подготовку агрегата к выполнению следующей операции.
Г — время, затрачиваемое на подготовку агрегата к выполнению следующей операции.
В данном случае предполагается, что дополнительные простои оборудования исключаются либо включены в  Г.
Г.
Время, затрачиваемое на подготовку агрегата к выполнению следующей операции, обычно является случайной величиной с показательным законом распределения
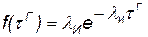 , (4.5)
, (4.5)
где λИ— интенсивность отказов, зависящая от характеристик обрабатывающего агрегата и реже от характеристик обслуживаемого ЛА.
Время выполнения операции обработки зависит обычно как от свойств обрабатывающего агрегата, так и от параметров обслуживаемого ЛА или его элемента. Если обрабатывающий агрегат функционирует нормально и случайные колебания величины 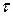 несущественны, то длительность операции обработки является фиксированной неслучайной величиной. В более общем виде
несущественны, то длительность операции обработки является фиксированной неслучайной величиной. В более общем виде 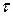 представляет собой случайную величину, вероятностные характеристики которой определяют в предположении независимости ее от других случайных величин с точностью до двух моментов, т.е. находятся ее среднее значение и дисперсия.
представляет собой случайную величину, вероятностные характеристики которой определяют в предположении независимости ее от других случайных величин с точностью до двух моментов, т.е. находятся ее среднее значение и дисперсия.
Рассмотрим следующую формализованную схему операций обработки. Обслуживаемый ЛА с номером j поступает к i -му обрабатывающему агрегату в момент tjН и имеет параметры аj1K. Если обрабатывающий агрегат свободен, то он в момент tjH приступает к обработке ЛА. В противном случае ЛА неограниченное время ожидает освобождения агрегата. Когда количество m аппаратов в очереди достигает lоч, подача их к обрабатывающему агрегату прекращается. Возобновление подачи ЛА производится по признаку m < l1. Операция обработки продолжается случайное время tопi, зависящее от 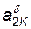 и длительности работы обрабатывающего агрегата после наладки
и длительности работы обрабатывающего агрегата после наладки 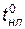 . Наладка обрабатывающего агрегата начинается по времени
. Наладка обрабатывающего агрегата начинается по времени  и продолжается tнл. Когда время t от начала процесса достигает значения Т, обработка нового ЛА не производится. Момент окончания операции обработки tK определяется по известным tН и времени занятости агрегата tзн (с учетом toп, возможного ремонта, наладки и доработки). Таким же образом определяется и момент готовности агрегата к обработке нового ЛА: TГ=tK + tГ, где tГ — случайная величина, имеющая смысл времени подготовки агрегата к операции.
и продолжается tнл. Когда время t от начала процесса достигает значения Т, обработка нового ЛА не производится. Момент окончания операции обработки tK определяется по известным tН и времени занятости агрегата tзн (с учетом toп, возможного ремонта, наладки и доработки). Таким же образом определяется и момент готовности агрегата к обработке нового ЛА: TГ=tK + tГ, где tГ — случайная величина, имеющая смысл времени подготовки агрегата к операции.
Блок-схема алгоритма операции обработки представлена на рис. 4.2.
Для построения алгоритма, моделирующего описанную операцию обработки, введены следующие операторы:
Ф1 — формирование очередного момента tjП поступления ЛА к агрегату;
Р2 — проверка условия tjП < tГ;
Р3 — проверка условия m > 1;
К4 — счетчик количества m ЛА в очереди, реализующий операцию m+ 1;
А5 — запись величин tjП в специальные ячейки;
F6 — переход к обработке очередного Л А;
F7 — формирование tj;
 ;
;
Ф9 — формирование значения tоп;
А10 — определение tKj (tKj = tНj+tзн);
А11 — подсчет наработки агрегата ;
;
Р12 — проверка условия  ;
;
Ф13 — формирование времени наладки tнл и конца наладки Тнл;
Ф14 — формирование случайных значений tГ;
А15 — определение момента ТГ;
Ф16 — формирование значений параметров ЛА после обработки;
K17 — подсчет количества обработанных ЛА;
F18 — формирование момента готовности агрегата ТГ;
К19 — счетчик количества ЛА в очереди, реализующий операцию m -1;
P20 — проверка условия β > 0 (β = 0 означает, что подача ЛА прекращена; β = 1 — подача производится);
Р21 — проверка условия m < l1;
F22 — формирование признака β = 1;
Р23 — проверка условия m < lоч;
F24 — формирование признака β = 0;
А25 — обработка результатов моделирования;
Я26 — окончание вычислений и выдача результатов.
Приведенный моделирующий алгоритм операции обработки состоит из двух частей. Первая часть, моделирующая непосредственно операцию обработки, начинается оператором Ф9 и заканчивается Ф16. Рассматривать ее, однако, удобнее с операторов F6,, F7 и P8.
Если условие, проверяемое оператором, P8(tHj < Т) выполнено, то управление передается оператору Ф9. В результате работы операторов Ф9 и Ф10 формируются tjоп и tjK.
Далее переходим к проверке условия 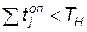 (операторы А11 и Р12), т. е. к проверке необходимости наладки обрабатывающего агрегата из-за износа. Если условие, проверяемое Р12, выполнено (в наладке необходимости нет), то переходим к формированию времени подготовки агрегата к следующей операции (оператор Ф14) после i -1 операции, определению момента готовности агрегата к обработке нового элемента ЛА (оператор А15) и формированию значений параметров элемента ЛА после обработки (оператор Ф16). В случае наладки агрегата (условие, проверяемое оператором Р12, не выполнено, оператор Ф13 формирует время наладки tнал и конца наладки Тнал и передает управления оператору А15 для определения готовности агрегата к обработке нового элемента ЛА.
(операторы А11 и Р12), т. е. к проверке необходимости наладки обрабатывающего агрегата из-за износа. Если условие, проверяемое Р12, выполнено (в наладке необходимости нет), то переходим к формированию времени подготовки агрегата к следующей операции (оператор Ф14) после i -1 операции, определению момента готовности агрегата к обработке нового элемента ЛА (оператор А15) и формированию значений параметров элемента ЛА после обработки (оператор Ф16). В случае наладки агрегата (условие, проверяемое оператором Р12, не выполнено, оператор Ф13 формирует время наладки tнал и конца наладки Тнал и передает управления оператору А15 для определения готовности агрегата к обработке нового элемента ЛА.
Вторая часть алгоритма непосредственно операцию обработки не моделирует, а обеспечивает связь и синхронизацию ее с другими актами технологического процесса подготовки ЛА (подача необработанных элементов ЛА), а также управление самим процессом моделирования (фиксация и обработка результатов, переход к очередному обрабатываемому элементу и т. д.). Эта часть алгоритма моделирует некоторую систему массового обслуживания. Оператор Ф1 формирует случайные числа tjП, которые имитируют поток однородных событий в соответствии с заданным законом распределения. Оператор Р2 проверяет условие tjП < ТГ. Если это условие выполнено, то заявка поступает в систему и обслуживается.
Операторная схема алгоритма, моделирующего работу обрабатывающего агрегата, запишется в виде
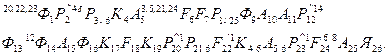
В операторной схеме приняты следующие обозначения:
ANК — арифметический оператор, означающий, что от оператора AN управления передается к оператору К;
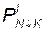 — логический оператор, означающий, что от оператора PN управление следует передавать оператору l, если условие, проверяемое
— логический оператор, означающий, что от оператора PN управление следует передавать оператору l, если условие, проверяемое
РN, выполнено, или же оператору К, если оно не выполнено;
n,lФN означает, что оператору формирования случайных процессов ФN управление передается от операторов n и I;
FN — операторы формирования неслучайных величин;
КN - счетчики.
В блок-схеме логический оператор обозначен ромбом, внутри которого записано проверяемое условие. Управление от логического оператора передается по стрелке, отмеченной единицей, если условие, проверяемое оператором, выполнено, и по стрелке, отмеченной нулем, если оно оказывается невыполненным.
Если появится необходимость в описании модифицированного процесса обработки, представленный алгоритм может быть легко видоизменен или дополнен другими операторами [25, 26].
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 325; Нарушение авторских прав?; Мы поможем в написании вашей работы!