Моделировании

Использование математических методов в макроэкономическом

Методы математического моделирования всегда находили широкое применение в естественных науках и только относительно недавно получили применение в экономике. Впервые они начали разрабатываться в рамках так называемого маржинализма – неоклассического направления в политической экономии, главным содержанием которого является теория предельной полезности. В ходе развития неоклассического направления постепенно осуществился переход от социально-экономической проблематики к общим проблемам функционирования экономических систем, рыночных и ценовых механизмов, реализации принципа экономичности и рациональности в условиях совершенной конкуренции, условий частного и общего равновесия. Родоначальником математической школы считается французский ученый О. Курно (1801 – 1877). В 1838 г. вышла его книга «Исследование математических принципов теории богатства» (О. Курно был известным математиком, философом, историком и экономистом).

Основным научным результатом неоклассического направления является разработка моделей частного и общего равновесия, условий использования ресурсов и их оптимального распределения по различным направлениям, условий равновесия обмена и потребления. Сюда относятся разработка моделей поведения потребителя, построение функций спроса, зависимостей спроса от цен и дохода, построение производственной функции, моделей поведения фирмы, моделей общего экономического равновесия.

В 1931 г. было создано международное эконометрическое общество. Термин «эконометрика» норвежский ученый Р. Фриш (1895 – 1973) ввел для обозначения направления, которое должно было представлять синтез экономической теории, математики и статистики. В дальнейшем круг проблем, разрабатываемых в рамках данного направления, сузился и сегодня в понятие «эконометрика» включается главным образом построение математико-статистических моделей экономических процессов (так называемых эконометрических моделей), использование методов математической статистики для определения параметров этих моделей.

Вторым важным направлением развития методов математического моделирования в экономике является теория исследования операций и принятия решений, большая роль в развитии которой принадлежит советским ученым: Л. В. Канторовичу, В. В. Новожилову, В. С. Немчинову, В. Леонтьеву. Предметом ее исследования являются задачи эффективного управления организационными системами. Такие задачи часто связаны с оптимизацией прибыли, себестоимости, трудозатрат и т. д. при наличии некоторых ограничений на использование ресурсов. Оптимизационные модели разного характера, как правило, сводятся к задачам линейного программирования.

Единой системы классификации экономико-математических моделей не существует. Для стратификации их на виды могут использоваться различные основания. По степени агрегирования объектов моделирования модели экономических систем разделяются на макроэкономические и микроэкономические. Хотя четко разграничения между ними нет, к первым принято относить модели, отражающие функционирование экономики как единого целого, в то время как ко вторым относят модели деятельности отдельных фирм, предприятий, организаций.

В настоящей главе будут кратко охарактеризованы два класса математических моделей в экономике, которые мы будем называть эконометрическими (ЭМ) и оптимизационными (ОМ).

Эконометрические модели. Математические исследования, которые проводятся в курсах “Макроэкономика”, “Микроэкономика”, “Экономическая теория” при изучении производственных функций, функций спроса и предложения, зависимости уровня безработицы от инфляции и т.п. носят качественный характер. Позволяя понять, каким образом те или иные параметры в целом влияют на экономические показатели, они не дают возможности анализировать реальные процессы в экономике. Во-первых, потому, что последние формируются под действием такого множества факторов, что они в принципе не могут быть учтены одновременно, во-вторых, не все эти факторы доступны прямому внешнему контролю. Неконтролируемые (неучтенные) факторы обусловливают случайность данных, которые они определяют. Например, производительность труда работника из общих соображений зависит от его квалификации, стажа работы, но также еще и от того женат ли он, владеет ли акциями предприятия, на котором работает, и любит ли футбол. Эти факторы являются случайными и никак не могут быть учтены в рамках аналитического подхода. Поскольку сама природа экономических данных носит статистический характер, то, очевидно, что для их анализа должны применяться специальные методы, которыми собственно и оперирует эконометрия.

Эконометрия - это наука, изучающая количественные закономерности и взаимосвязи в экономике методами математической статистики. Целью эконометрии является эмпирический вывод экономических законов, а основным инструментом – построение ЭМ с последующей их верификацией. Эконометрический анализ служит основой для экономического анализа и краткосрочного прогнозирования.

Методологическая особенность эконометрии заключается в применении общих гипотез о статистических свойствах экономических параметров и ошибок при их измерении. Полученные при этом результаты могут оказаться нетождественными тому содержанию, которое вкладывается в реальный объект. Поэтому важная задача эконометрики – создание как более универсальных, так и специальных методов для обнаружения наиболее устойчивых характеристик в поведении реальных экономических показателей. Эконометрия разрабатывает методы «подгонки» формальной модели с целью наилучшего имитирования ею поведения моделируемого объекта на основе гипотезы о том, что отклонение модельных параметров от реально наблюдаемых случайны и вероятностные характеристики их известны.

Главным инструментом эконометрии служит эконометрическая модель – модель факторного анализа, параметры которой оцениваются средствами математической статистики. Такая модель выступает в качестве средства анализа и прогнозирования конкретных экономических процессов на основе реальной статистической информации.

Статистической или корреляционной зависимостью называется связь переменных, на которую накладывается действие случайных факторов, причем изменение одной переменной приводит к изменению математического ожидания (среднего значения) другой. Эконометрия является лишь инструментом для изучения статистических зависимостей между экономическими показателями и не ставит своей целью установление причинно-следственных связей между ними.

К числу типичных экономико-математических моделей, которые разрабатывает и изучает эконометрия, относятся производственные функции, функции спроса, целевые функции потребления разных групп потребителей, статические и динамические межотраслевые модели производства. Общие объекты исследования тесно связывают макро- и микроэкономику с эконометрией. Таким образом, два подхода (условно назовем их качественным и количественным) взаимно дополняют друг друга, и только их совместное применение может обеспечить хорошие результаты.

Каждое эконометрическое исследование проводится в рамках некоторой модели – умозрительной конструкции, выделяющей главные, существенные стороны интересующего исследователя фрагмента экономического мира и отбрасывающей те, которые представляются незначимыми.

Как уже отмечалось выше, связь между различными явлениями в экономике сложна и разнообразна. На уровень одного показателя могут влиять с разной интенсивностью множество факторов. Для изучения формы связи между показателем и факторами на основе статистических данных используется регрессионный анализ, лежащий в основе эконометрического подхода.

Эконометрическая модель, оперирует с числовыми выборочными данными, характеризующими изучаемые экономические величины, и, как правило, представленными в виде таблицы. Выборочными они называются потому, что представляют собой выборку (или часть) генеральной совокупности – множества всех значений, которые может принимать исследуемый фактор. Данные в ЭМ бывают двух типов: пространственные и временные. Пространственные данные – это данные по какому-либо экономическому показателю, полученные на разных однотипных объектах (странах, предприятиях, отраслях) в один момент времени; временные данные характеризуют один и тот же объект в разные моменты времени, например, ежесуточные данные по индексу Доу-Джонса, ежегодные данные по урожайности пшеницы и т.п.

В наиболее общем виде ЭМ можно записать в виде:

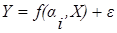
где 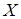- независимая переменная (или фактор); 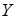- зависимая переменная (или показатель); 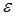- случайная переменная, учитывающая воздействие на 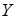других, неучтенных в уравнении факторов; a_i – параметры уравнения, поиск которых и является основной задачей моделирования.

Обычно предполагается, что все факторы, неучтенные явно в модели, в сумме описываются именно случайной переменной. Построить ЭМ – значит установить наличие или отсутствие связи между 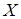и 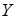, а также вид этой связи (функциональной зависимости). При этом ЭМ варьируется по определенным показателям.

1. По наличию либо отсутствию причинно-следственной связи:

- переменные 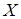и 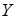не разделяются на первичную и вторичную, то есть 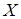и 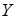можно поменять местами. Такими парами, например, являются средняя зарплата на предприятии и количество работников на нем; объемы добычи в стране нефти и железной руды и т.п. Эконометрия позволяет включать в экономическую модель подобные переменные, связь между которыми является не прямой, а опосредованной;

- изменение 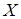является причиной изменения 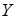, что следует, например, из макроэкономических моделей. К таким переменным относятся, например, курс валюты страны и сбалансированность внешней торговли; инвестиции в предприятия и объемы производства на нем. При этом, поскольку изменение 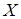приводит к неодинаковому изменению 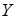на разных исследуемых объектах (одинаковые инвестиции в разные предприятия приводят к разным результатам), то анализировать можно только влияние 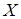на среднее значение (математическое ожидание) 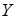, таким образом, применение методов регрессионного анализа является оправданным.

2. По количеству факторов в модели: формула статистической связи двух переменных (зависимой и независимой) называется парной или простой регрессией, при нескольких независимых переменных – множественной регрессией (в этом случае следует писать X_i, i = 1… n; n – число независимых переменных).

3. По виду функциональной зависимости 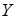(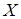) (линейная, нелинейная).

В простейшей модели парной линейной регрессии зависимость между переменными в генеральной совокупности представляется в виде:

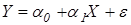
По данным выборки (y_i, x_i) строится выборочное уравнение регрессии:

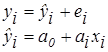
где 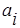– оценки параметров 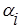; 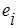- оценка ошибки 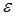. Линейная модель – самая распространенная ЭМ. Тем на менее, часто приходится иметь дело и с нелинейными моделями (например, при моделировании производственной функции Кобба-Дугласа). Нелинейность регрессии может проявляться как по переменным, так и по параметрам. Нелинейность по переменным устраняется путем замены переменной. Например, нелинейное гиперболическое уравнение 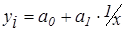приводится к линейному путем замены 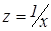. Нелинейность по параметру часто устраняется путем логарифмирования левой и правой части уравнения. Например, следующие нелинейные уравнения после логарифмирования сводятся к линейным:

- степенная функция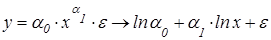

- экспонента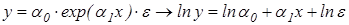

Поиск параметров 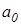, 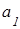обычно проводится по методу наименьших квадратов (МНК), обеспечивающему наилучшее приближение набора эмпирических данных линейным уравнением. Суть данного метода заключается в том, что минимизируется квадрат суммы разностей между фактическим значением признака и его теоретическим значением (см. рис.А.1):

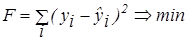
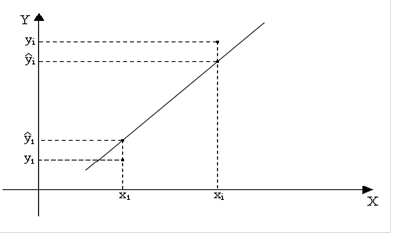
Рисунок А.1 – МНК для однофакторной линейной регрессии

Для однофакторной линейной регрессии выражения для 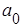, 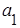имеют вид:

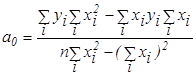
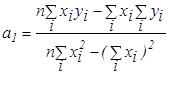
Дальнейшие действия по построению ЭМ заключаются в проверке качества модели. На этом этапе оцениваются статистическая значимость параметров 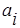по отдельности и значимость модели в целом. Кроме того, модель проверяется на:

- мультиколлинеарность – наличие корреляции двух или более независимых переменных в уравнении регрессии; при ее наличии МНК-оценки параметров 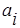имеют большие стандартные ошибки и малую значимость;

- гетероскедастичность (см. рис.А.2) – зависимость дисперсии случайного члена 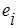(3) от номера наблюдения i, приводит к неэффективности оценок параметров ;

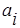- автокорреляцию остатков (см. рис.А.3) – наличие корреляции между случайными членами 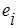, которая также приводит к неэффективности оценок параметров .

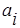Существуют специальные методы диагностирования и устранения гетероскедастичности и автокорреляции остатков. При обнаружении мультиколлинеарности необходимо исключить из модели те из взаимозависимых факторов, которые оказывают относительно меньшее влияние на признак.

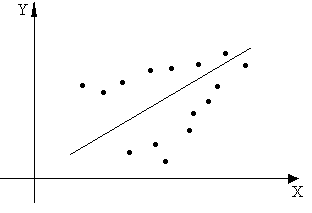
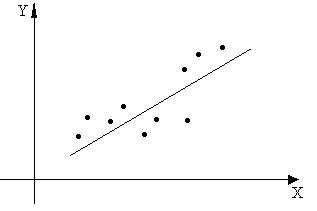
Рисунок А.2 – Гетероскедастичность Рисунок А.3 – Автокорреляция остатков

Математическая статистика является тем универсальным аппаратом, который удачно вписывается в содержание различных эконометрических исследований. Такие ее разделы, как корреляционный и регрессионный анализ, метод наименьших квадратов и прогнозирование как нельзя лучше подходят для выявления статистических закономерностей в экономике.

Корреляционный анали з позволяет количественно оценить связи между большим числом взаимодействующих экономических явлений как между случайными величинами или группой величин. Корреляционный анализ тесно связан с регрессионным анализом, задача которого состоит в экспериментальном определении параметров корреляционных зависимостей между экономическими показателями путем наблюдений за характером их изменений. Одним из основных методов определения параметров регрессионных уравнений в рамках регрессионного анализа является метод наименьших квадратов. Модели, составленные с помощью применения регрессионного анализа, позволяют прогнозировать варианты развития экономических явлений и процессов, изучать тенденции изменения экономических показателей.

Таким образом, можно обозначить следующие этапы построения ЭМ:

1. Анализ экономической проблемы, качественное рассмотрение возможных взаимосвязей между переменными, входящими в задачу.

2. Подготовка данных, подбор математической функции, предположительно описывающей связь между показателем и факторами модели.

3. Оценка параметров модели.

4. Верификация модели (проверка значимости параметров, модели в целом, анализ остатков e_i).

5. Подгонка эконометрической модели (корректирование набора факторов, уточнение функции, описывающей их связь с показателем).

6. Составление прогноза на базе построенной ЭМ – оценка независимой переменной для некоторого набора независимых переменных, которых нет в исходных наблюдениях.

Особое внимание следует обратить на построение системы показателей и определение совокупности факторов, влияющих на каждый из показателей. К включаемым в эконометрическую модель факторам предъявляются следующие требования:

- включение каждого фактора в модель должно быть обосновано теоретически;

- целесообразно учитывать только те факторы, которые оказывают существенное влияние на изучаемые показатели, при этом рекомендуется, чтобы количество включаемых в модель факторов не превышало одной трети от числа наблюдений в выборке;

- между факторами не должно существовать линейной зависимости, поскольку ее наличие будет означать, что они характеризуют влияние одной и той же по сути причины на показатель. Например, размер заработной платы работников зависит, в том числе, и от роста производительности труда и от объема выпускаемой продукции. Однако эти два фактора могут быть тесно взаимосвязаны, коррелированны, следовательно, в модель целесообразно включить лишь один из них. Включение в модель линейно зависимых факторов приводит к возникновению мультиколлинеарности, которая отрицательно сказывается на качестве модели;

- в модель рекомендуется включать только те факторы, которые могут быть измерены количественно;

- в одну модель не следует включать какой-либо фактор одновременно с образующими его частными факторами. Это приведет к не соответствующему реальности увеличению их влияния на зависимые переменные модели и, как следствие, к искажению отображения реальной действительности.

При отборе факторов, влияющих на зависимые переменные модели, используются статистические методы отбора. Так, существенного сокращения числа факторов (а значит – сделать модель менее громоздкой) можно достичь с помощью применения пошаговых процедур отбора переменных. Их можно сочетать и с другими подходами к решению проблемы, например, с экспертными методами оценки значимость факторов.

Метод исключения предполагает построение уравнения, включающего некоторую начальную совокупность переменных с последующим последовательным сокращением их числа до тех пор, пока не будет выполнено заданное изначально при составлении уравнения условие. Применение метода включения подразумевает последовательное включение в модель все новых переменных, пока модель не станет соответствовать установленному критерию качества модели. Последовательность включения переменных в модель определяется с помощью частных коэффициентов корреляции: те переменные, для которых значение такого коэффициента, показывающего их связь с исследуемым показателем, больше, чем для прочих, включаются в регрессионное уравнение в первую очередь.

Разработка эконометрических моделей воплощает в себе применение функционального подхода к описанию систем. Эконометрические модели по сравнению с аналитическими более точны и подробны, не требуют грубых допущений, позволяют учесть большое количество факторов. Основные их недостатки – с целью быть точными в учете факторов, они часто громоздки, имеют плохую обозримость, большой расход машинного времени при их построении и анализе; крайняя трудность поиска оптимальных решений (что от них, по большому счету, и не требуется), которые требуется искать путем проб и ошибок (в отличие от более приспособленных к применению оптимизационных процедур аналитических моделей). Наиболее эффективным в свете этого является не изолированная, а совместная разработка и использование аналитических и эконометрических моделей.

Реальные эконометрические задачи могут включать значительное (иногда десятки и сотни) число уравнений и переменных, тем не менее, для демонстрации схемы построения ЭМ достаточно привести следующую упрощенную модель.

Дата добавления: 2014-10-15