Основные теоретические сведения. Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение

Случайной величиной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Случайные величины делятся на дискретные и непрерывные.

Дискретной (прерывной) случайной величинойназывается случайная величина, которая принимает отдельные, изолированные возможные значения с определёнными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Непрерывной случайной величинойназывается случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений непрерывной случайной величины бесконечно.

Законом распределения случайной величиныназывается всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она «распределена» по данному закону распределения или «подчинена» этому закону распределения. Для дискретной случайной величины закон распределения может быть задан в виде таблицы, аналитически (в виде формулы) и графически. Простейшей формой задания закона распределения дискретной случайной величины 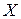является таблица, в которой перечислены в порядке возрастания все возможные значения случайной величины и соответствующие их вероятности:

			…		…
			…		…

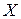
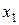
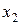
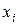
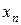
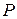
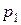
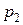
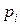
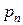
Такая таблица называется рядом распределения дискретной случайной величины. События 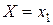, , 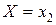…, 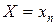состоящие в том, что в результате испытания случайная величина 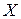примет соответственно значения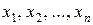, являются несовместными и единственно возможными (так как в таблице перечислены все возможные значения случайной величины), то есть образуют полную группу. Следовательно, сумма их вероятностей равна единице. Таким образом, для любой дискретной случайной величины:

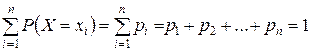(1)

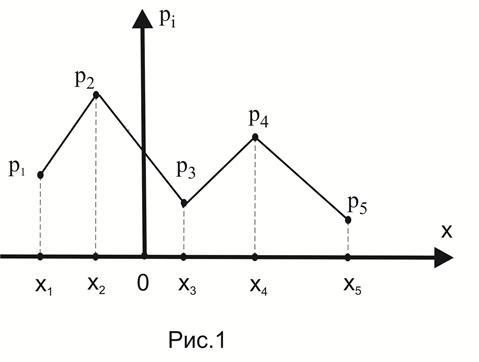
Многоугольником распределения (полигоном) вероятностей дискретной случайной величины называется ломаная, состоящая из отрезков, соединяющих точки с координатами 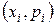(см. рис.1). Многоугольник распределенияпредставляет собой графическое изображение ряда распределения.

Функцией распределения случайной величины 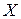называется функция 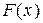, определяющая вероятность того, что случайная величина 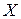в результате испытания примет значение, меньшее :

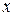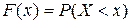, (2)

где 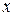- текущая переменная.

Функцию 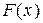также называют интегральной функцией распределения или интегральным законом распределения. Геометрически функция распределения интерпретируется как вероятность того, что случайная точка 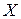попадёт левее заданной точки 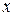(см. рис.2)

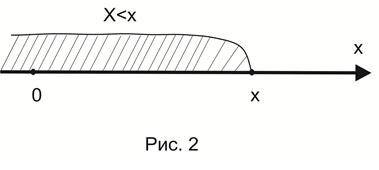
Функция распределения обладает следующими свойствами:

1.) Функция распределения случайной величины есть неотрицательная функция, заключённая между нулём и единицей:

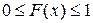(3)

2.) Функция распределения случайной величины есть неубывающая функция на всей числовой оси.

3.) На минус бесконечности функция распределения равна нулю, на плюс бесконечности равна единице:

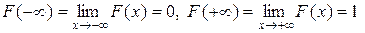(4)

4.) Вероятность попадания случайной величины в интервал 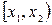равна приращению её функции распределения на этом интервале:

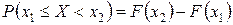(5)

Исходя из определения и свойств функции распределения, для дискретной случайной величины, заданной рядом распределения и имеющей 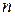значений получаем:

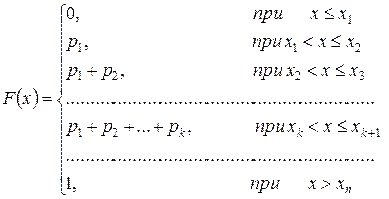(6)

График функции распределения дискретной случайной величины представляет собой совокупность горизонтальных отрезков, длина которых равна длине интервалов 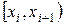. Если ввести обозначения для формулы (6):

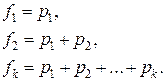(7)

то получим график, изображённый на рис.3.

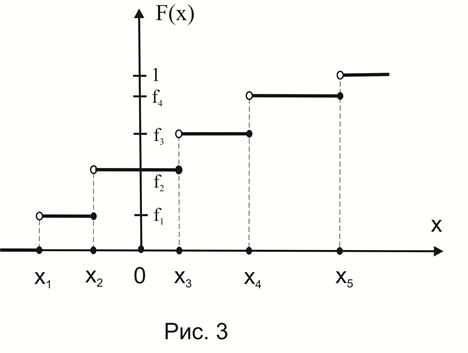
После введения понятия функции распределения можно дать ещё одно, более точное, определение понятия непрерывной случайной величины:

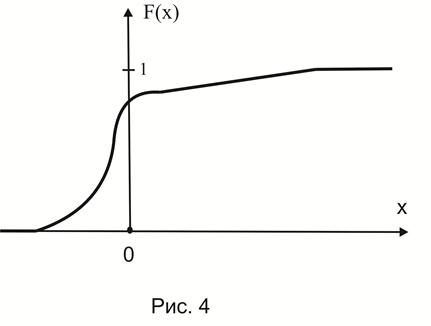
Случайная величина называется непрерывной, если её функция распределения непрерывна в любой точке и дифференцируема всюду, кроме быть может отдельных точек. Один из возможных примеров графика функции распределения непрерывной случайной величины представлен на рис.4.

Плотностью вероятности (плотностью распределения или просто плотностью) непрерывной случайной величины 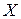называется производная от её функции распределения:

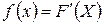(8)

Плотность вероятности называют также дифференциальной функцией распределения или дифференциальным законом распределения. Для дискретной случайной величины понятия плотности распределения не существует.

Плотность распределения вероятностей непрерывной случайной величины обладает следующими свойствами:

1.) Плотность вероятности – неотрицательная функция:

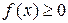(9)

2.) Вероятность попадания непрерывной случайной величины в интервал 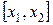равна определённому интегралу от её плотности вероятности в пределах от 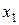до :

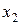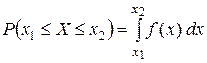(10)

3.) Функция распределения непрерывной случайной величины может быть выражена через плотность вероятности по формуле:

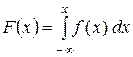(11)

4.) Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

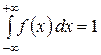(12)

Один из возможных примеров графика плотности распределения непрерывной случайной величины представлен на рис.5.

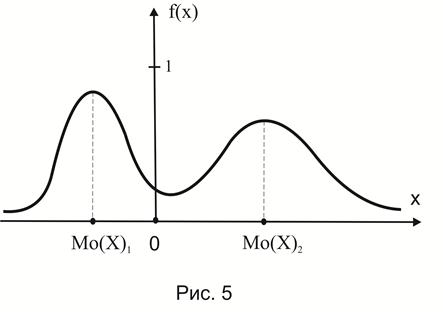
График плотности вероятности 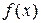называется кривой распределения.

Числовыми характеристиками (параметрами распределения) случайной величиныназываются числа, которые описывают случайную величину суммарно, то есть сразу в целом всё распределение, а не отдельные значения случайной величины. К ним относятся: математическое ожидание, дисперсия, среднее квадратическое отклонение, мода и т.д. Рассмотрим некоторые из них.

Математическим ожиданием дискретной случайной величины 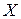называют сумму произведений всех её возможных значений на их вероятности:

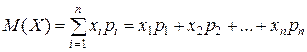(13)

Математическим ожиданием непрерывной случайной величины 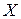, возможные значения которой принадлежат всей оси 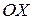, называют определённый интеграл:

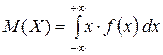(14)

Отклонением случайной величины от её математического ожидания называется разность между случайной величиной и её математическим ожиданием:

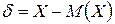(15)

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

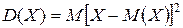(16)

Для дискретной случайной величины формула (16) приобретает вид:

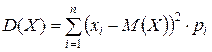(17)

Для непрерывной случайной величины формула (16) приобретает вид:

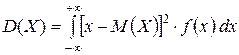(18)

Дисперсию случайной величины также можно посчитать по-другому: дисперсия равна разности между математическим ожиданием квадрата случайной величины 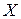и квадратом её математического ожидания:

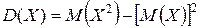(19)

Для дискретной случайной величины формула (19) приобретает вид:

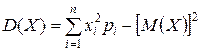(20)

Для непрерывной случайной величины формула (19) приобретает вид:

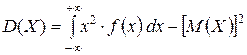(21)

Средним квадратическим отклонением (стандартным отклонением или стандартом) случайной величины 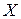называется арифметическое значение корня квадратного из её дисперсии:

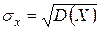(22)

Модой 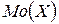дискретной случайной величины 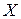называется её значение 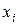, принимаемое с наибольшей вероятностью по сравнению с двумя соседними значениями. Если все значения дискретной случайной величины 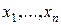расположены в порядке возрастания, то для вероятности модального значения 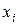выполняются неравенства:

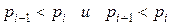(23)

Модой 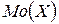непрерывной случайной величины называют точку локального максимума плотности распределения .

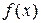Если вероятность (для дискретной случайной величины) или плотность (для непрерывных случайных величин) достигает максимума только в одной точке, то распределение называется унимодальным (одномодальным). Если в в двух разных точках – то бимодальным (двухмодальным), и вообще, если в нескольких точках, то распределение называется полимодальным (мультимодальным). Например, распределение дискретной случайной величины, представленное на рис.1 имеет две моды 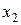и 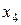, следовательно, оно является бимодальным или полимодальным. Распределение непрерывной случайной величины, представленное на рис.5 имеет две моды и 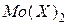, следовательно, оно является бимодальным или полимодальным.

Наивероятнейшим значением случайной величины называют моду, при которой достигается глобальный максимум вероятности (дискретной случайной величины) или плотности распределения (непрерывной случайной величины).

Медианой 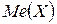непрерывной случайной величины 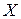называется такое её значение, для которого вероятность того, что случайная величина 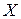примет значение, меньшее медианы или большее её, одна и та же и равна 0.5:

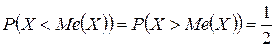(24)

Для непрерывных случайных величин вертикальная прямая 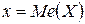делит площадь фигуры под кривой распределения на две равные части. И очевидно, что в точке 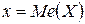функция распределения равна 0.5.

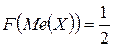(25)

Дата добавления: 2014-10-23