
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Образец выполнения лабораторной работы
|
|
|
|
Порядок выполнения лабораторной работы.
1. Найти функцию распределения дискретной случайной величины и построить её график.
2. Вычислить математическое ожидание дискретной случайной величины.
3. Вычислить дисперсию дискретной случайной величины двумя способами (по формулам (17) и (20)) и сравнить результаты.
4. Вычислить среднеквадратическое отклонение дискретной случайной величины.
5. Найти моду (моды) дискретной случайной величины.
6. Найти функцию распределения непрерывной случайной величины.
7. Начертить график плотности распределения непрерывной случайной величины.
8. Начертить график функции распределения непрерывной случайной величины.
9. Вычислить математическое ожидание непрерывной случайной величины.
10. Вычислить дисперсию непрерывной случайной величины.
11. Вычислить среднеквадратическое отклонение непрерывной случайной величины.
12. Найти моду (моды) непрерывной случайной величины.
13. Найти медиану непрерывной случайной величины.
14. Изобразить медиану на графике плотности рапределения.
Запускаем OpenOffice и выбираем приложение «Электронная таблица». Открываем файл, соответствующий номеру варианта. Загружается файл с данными. (Можно просто щёлкнуть мышью по файлу, соответствующему номеру варианта). В середине поля электронной таблицы расположены данные по дискретному распределению в Вашем варианте. Фрагмент середины поля электронной таблицы приведён на рис.6.

Рис. 6
В лист отчёта поставьте цифру один и напишите «Обработка дискретной случайной величины». В первом столбце слева расположены значения дискретной случайной величины 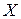 , во втором столбце соответствующие вероятности. Перепишем в лист отчёта таблицу представленную на рис.6. Найдём значения функции распределения
, во втором столбце соответствующие вероятности. Перепишем в лист отчёта таблицу представленную на рис.6. Найдём значения функции распределения 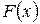 . Для этого в первую пустую ячейку столбца
. Для этого в первую пустую ячейку столбца 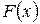 (сверху) запишем значение нуль. Для этого нужно щёлкнуть левой клавишей мыши на эту ячейку и набрать с клавиатуры символ 0. Затем щёлкнуть мышкой в следующую ячейку. Во вторую ячейку этого столбца необходимо вписать формулу. Если вторая ячейка выделена, то необходимо набрать с клавиатуры выражение:
(сверху) запишем значение нуль. Для этого нужно щёлкнуть левой клавишей мыши на эту ячейку и набрать с клавиатуры символ 0. Затем щёлкнуть мышкой в следующую ячейку. Во вторую ячейку этого столбца необходимо вписать формулу. Если вторая ячейка выделена, то необходимо набрать с клавиатуры выражение: 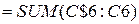 и нажать кнопку Enter на клавиатуре. После этого во второй ячейке должно появиться значение 0,1 – то есть вероятность
и нажать кнопку Enter на клавиатуре. После этого во второй ячейке должно появиться значение 0,1 – то есть вероятность 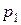 из второй колонки. В третьей ячейке сверху в третьей колонке вписываем выражение
из второй колонки. В третьей ячейке сверху в третьей колонке вписываем выражение 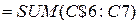 , что обозначает суммирование значений из второй колонки от строки
, что обозначает суммирование значений из второй колонки от строки 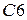 до строки
до строки 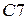 . Нажав Enter, видим, что в ячейке появилось значение 0,3. Теперь необходимо выделить сразу две ячейки в третьей колонке – те ячейки, в которых содержаться значения 0,1 и 0,3. Для этого, удерживая клавишу Ctrl нажатой, щёлкнем левой клавишей мыши по второй ячейке, а затем по третьей. При этом обе ячейки должны выделиться цветом. После этого, подводим указатель мышки к правому нижнему углу третьей ячейки, после этого в углу должен появиться крестик, как показано на рисунке 7.
. Нажав Enter, видим, что в ячейке появилось значение 0,3. Теперь необходимо выделить сразу две ячейки в третьей колонке – те ячейки, в которых содержаться значения 0,1 и 0,3. Для этого, удерживая клавишу Ctrl нажатой, щёлкнем левой клавишей мыши по второй ячейке, а затем по третьей. При этом обе ячейки должны выделиться цветом. После этого, подводим указатель мышки к правому нижнему углу третьей ячейки, после этого в углу должен появиться крестик, как показано на рисунке 7.
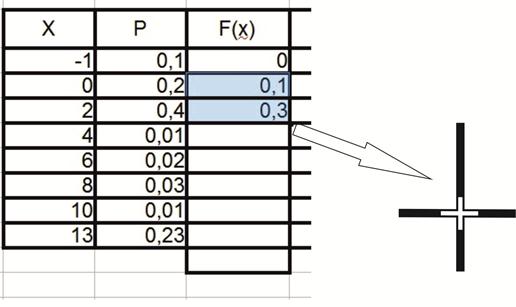
Рис.7
Нажав левую клавишу мыши, протянем область рамки выделения вниз до самой последней ячейки 3-ей колонки таблицы и отпустим левую клавишу мыши. В результате должны появиться числа, как показано на рисунке 8.
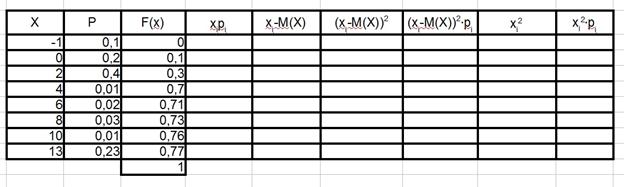
Рис.8
Проверьте правильность Ваших действий: в самой нижней ячейке должна получиться единица. Если это не так, то Вы что-то сделали неправильно. В лист отчёта ниже таблицы запишите подробно вычисление значений функции распределения по её свойствам и формулам (6,7), взяв уже вычисленные значения из колонки 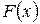 :
:
1.) Если 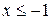 , то
, то 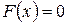 ;
; 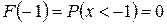 .
.
2.) Если 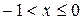 , то
, то 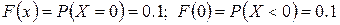 .
.
3.) Если  , то
, то 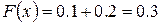
4.) Если 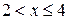 , то
, то 
5.) Если 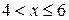 , то
, то 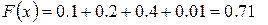
6.) Если 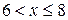 , то
, то 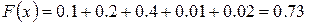
7.) Если 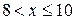 , то
, то 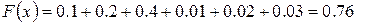
8.) Если 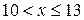 , то
, то 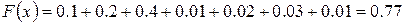
9.) Если 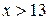 , то
, то 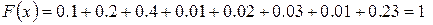
Используя форму записи как в формуле (7) запишем:
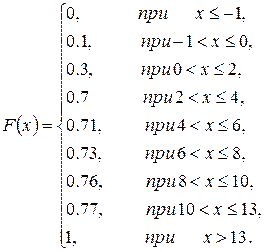
Ниже изобразим график функции распределения дискретной случайной величины, как мы это делали на рис.3. Получившийся график функции распределения в рассматриваемом примере приведён на рисунке 9.
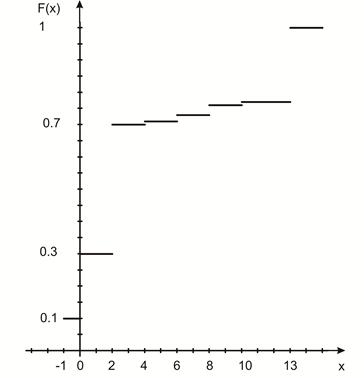
Рис. 9
Далее найдём математическое ожидание. Для этого посчитаем сначала произведения 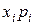 . В соответствующей колонке открытого приложения OpenOffice Calc (четвёртая колонка) щёлкнем левой клавишей мыши на пустую первую ячейку (сверху) и введём формулу
. В соответствующей колонке открытого приложения OpenOffice Calc (четвёртая колонка) щёлкнем левой клавишей мыши на пустую первую ячейку (сверху) и введём формулу 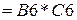 и нажмём Enter. В ячейке должно появиться число -0,1. Теперь снова щёлкнем левой клавишей мыши по этой ячейке и подведя указатель мыши к правому нижнему углу этой ячейки добьёмся появления в углу белого крестика. После этого нажмём левую клавишу мыши и протянем область обрамления до последней ячейки в колонке. Отпустим левую клавишу мыши и увидим результат вычисления (см. рис. 10.)
и нажмём Enter. В ячейке должно появиться число -0,1. Теперь снова щёлкнем левой клавишей мыши по этой ячейке и подведя указатель мыши к правому нижнему углу этой ячейки добьёмся появления в углу белого крестика. После этого нажмём левую клавишу мыши и протянем область обрамления до последней ячейки в колонке. Отпустим левую клавишу мыши и увидим результат вычисления (см. рис. 10.)
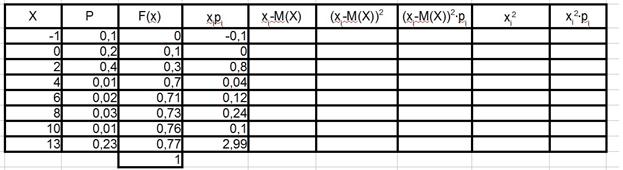
Рис.10
Перепишем с экрана полученные значения в таблицу в листе отчёта. Затем кликнув на первую ячейку (сверху) с числовым значением в колонке 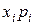 и удерживая левую кнопку мыши протянем область выделения цветом до самой нижней ячейки. После этого кликнем левой клавишей мыши на значёк
и удерживая левую кнопку мыши протянем область выделения цветом до самой нижней ячейки. После этого кликнем левой клавишей мыши на значёк  - значёк суммирования в меню OpenOffice Calc. В результате внизу колонки
- значёк суммирования в меню OpenOffice Calc. В результате внизу колонки 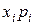 появится ещё одно числовое значение, которое и будет являться математическим ожиданием. В лист отчёта необходимо записать:
появится ещё одно числовое значение, которое и будет являться математическим ожиданием. В лист отчёта необходимо записать:
Используя формулу (13) получаем:
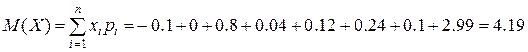
Теперь вычислим отклонения случайных величин от их математического ожидания, воспользовавшись формулой (15). Для этого кликнем мышью в первую пустую ячейку сверху в колонке 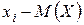 и введём формулу
и введём формулу 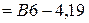 (в Вашем варианте не 4,19, а Ваше значение
(в Вашем варианте не 4,19, а Ваше значение 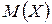 ) и нажмём Enter. В ячейке должно появиться значение -5,19 (В Вашем варианте – Ваше значение). Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения отклонений. Перепишем их в таблицу в листе отчёта. Теперь получим квадраты отклонений. Для этого в столбце
) и нажмём Enter. В ячейке должно появиться значение -5,19 (В Вашем варианте – Ваше значение). Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения отклонений. Перепишем их в таблицу в листе отчёта. Теперь получим квадраты отклонений. Для этого в столбце 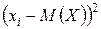 кликнем на первую свободную ячейку сверху и введём выражение
кликнем на первую свободную ячейку сверху и введём выражение 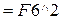 , нажмём Enter. Появится первое вычисленное значение квадрата отклонения 26,9361. Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения квадратов отклонений. Перепишем их в таблицу в листе отчёта. Теперь перемножим каждый квадрат отклонения на вероятность соответствующего значения случайной величины. Для этого в столбце
, нажмём Enter. Появится первое вычисленное значение квадрата отклонения 26,9361. Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения квадратов отклонений. Перепишем их в таблицу в листе отчёта. Теперь перемножим каждый квадрат отклонения на вероятность соответствующего значения случайной величины. Для этого в столбце 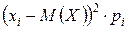 кликнем на первую свободную ячейку сверху и введём выражение
кликнем на первую свободную ячейку сверху и введём выражение 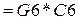 , нажмём Enter. Появится первое вычисленное значение 2,69361. Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения произведений. Перепишем их в таблицу в листе отчёта. Для вычисления дисперсии выделим все числовые значения колонки
, нажмём Enter. Появится первое вычисленное значение 2,69361. Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения произведений. Перепишем их в таблицу в листе отчёта. Для вычисления дисперсии выделим все числовые значения колонки 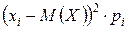 и нажмём на значёк
и нажмём на значёк 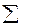 в меню OpenOffice Calc. В лист отчёта запишем: Используя формулу (17) получаем:
в меню OpenOffice Calc. В лист отчёта запишем: Используя формулу (17) получаем:
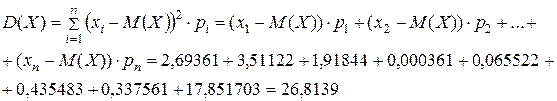
Теперь вычислим дисперсию по другой формуле. Для этого сначала посчитаем квадраты значений случайной величины. Для этого в столбце 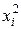 кликнем на первую свободную ячейку сверху и введём выражение
кликнем на первую свободную ячейку сверху и введём выражение 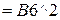 , нажмём Enter. Появится первое вычисленное значение 1. Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения квадратов. Перепишем их в таблицу в листе отчёта. Теперь посчитаем значения в столбце
, нажмём Enter. Появится первое вычисленное значение 1. Подведём указатель мыши к правому нижнему углу нижней ячейки так чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения квадратов. Перепишем их в таблицу в листе отчёта. Теперь посчитаем значения в столбце 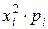 . Для этого в этом столбце кликнем на первую свободную ячейку сверху и введём выражение
. Для этого в этом столбце кликнем на первую свободную ячейку сверху и введём выражение 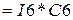 , нажмём Enter. Появится первое вычисленное значение 0,1. Подведём указатель мыши к правому нижнему углу нижней ячейки так, чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения произведений. Перепишем их в таблицу в листе отчёта. Для вычисления математического ожидания квадрата случайной величины выделим все числовые значения колонки
, нажмём Enter. Появится первое вычисленное значение 0,1. Подведём указатель мыши к правому нижнему углу нижней ячейки так, чтобы появился крестик и протянем выделенную область до самой нижней ячейки. В результате вычислим все значения произведений. Перепишем их в таблицу в листе отчёта. Для вычисления математического ожидания квадрата случайной величины выделим все числовые значения колонки 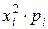 и нажмём на значёк
и нажмём на значёк  в меню OpenOffice Calc. И далее запишем в лист отчёта: найдём математическое ожидание квадрата случайной величины:
в меню OpenOffice Calc. И далее запишем в лист отчёта: найдём математическое ожидание квадрата случайной величины:
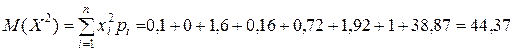
Теперь для вычисления по формуле (20) можно кликнуть мышкой в свободную ячейку ниже таблицы и написать туда выражение 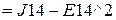 . В лист отчёта запишем: По формуле (20) получаем:
. В лист отчёта запишем: По формуле (20) получаем:
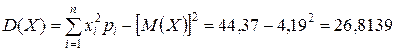
Таким образом, совпали значения дисперсии вычисленной по формуле (17) и по формуле (20). Для вычисления среднего квадратического отклонения в свободное поле ниже таблице кликнем мышкой и введём выражение 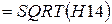 . В лист отчёта запишем: По формуле (22) вычислим среднее квадратическое отклонение:
. В лист отчёта запишем: По формуле (22) вычислим среднее квадратическое отклонение:
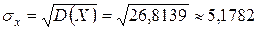
После всех вышеприведённых вычислений рабочее поле электронной таблицы выглядит, как показано на рисунке 11.
Построим полигон распределения, как это показано на рис.1. Для этого выделим цветом столбцы 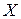 и
и 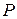 (только ячейки с числами) и кликнем мышью на значёк диаграммы в меню OpenOffice Calc. Открывается диалоговое окно мастера диаграмм. В поле «Выберете тип диаграммы» кликнете мышью на «Диаграмма XY». В окне, открывшемся справа,
(только ячейки с числами) и кликнем мышью на значёк диаграммы в меню OpenOffice Calc. Открывается диалоговое окно мастера диаграмм. В поле «Выберете тип диаграммы» кликнете мышью на «Диаграмма XY». В окне, открывшемся справа,
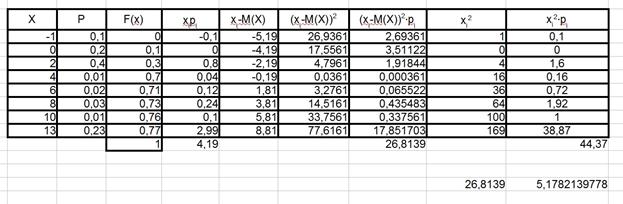
Рис.11
кликнете левой клавишей мыши на картинку с названием «Линии и точки». Затем нажмите «Готово». В результате на экране появится полигон распределения приведённый на рисунке 12.
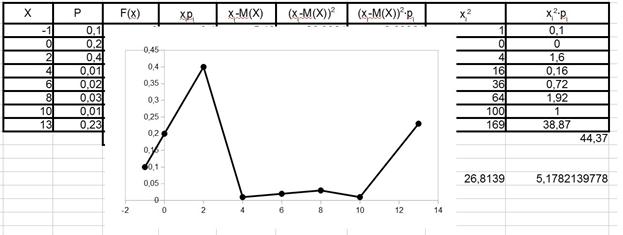
Рис.12
Перерисуем его в лист отчёта, не забывая подписывать оси. Теперь найдём моду дискретной случайной величины. Исходя из определения моды для дискретной случайной величины, по полигону распределения видно, что модами будут являться: 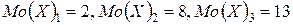 . Таким образом, данное распределение является полимодальным (мультимодальным).
. Таким образом, данное распределение является полимодальным (мультимодальным).
В лист отчёта поставьте цифру два и напишите «Обработка непрерывной случайной величины». Выполнение этой части работы производится без компьютера. Компьютер может быть использован лишь для арифметических расчётов с помощью калькулятора, встроенного в операционную систему.
Выписываем в лист отчёта плотность распределения непрерывной случайной величины из варианта заданий.
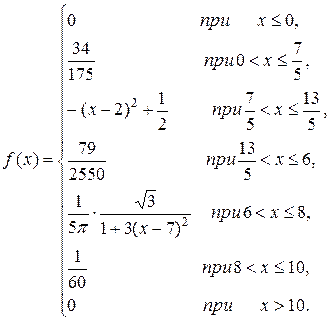
Найдём значения функции распределения 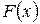 . Для этого воспользуемся формулой (11) и свойствами функции распределения. В соответствии с интервалами разобьём решение на пункты:
. Для этого воспользуемся формулой (11) и свойствами функции распределения. В соответствии с интервалами разобьём решение на пункты:
а) если 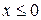 , то
, то 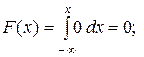
б) если 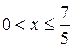 , то
, то 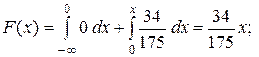
в) если  , то
, то 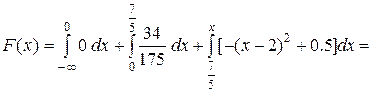
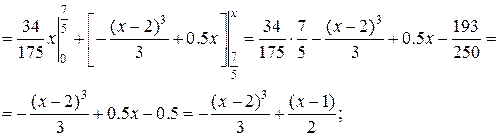
г) если  , то
, то 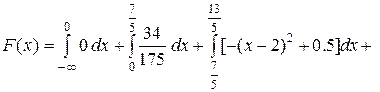

д) если 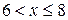 , то
, то 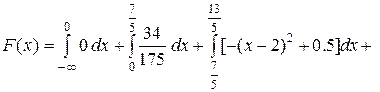
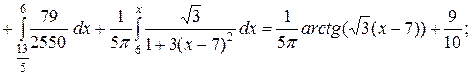
е) если 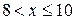 , то
, то 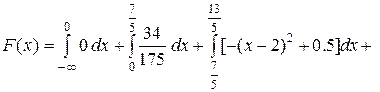

ё) если 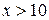 , то
, то 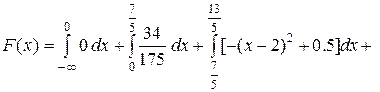

Таким образом, получаем:
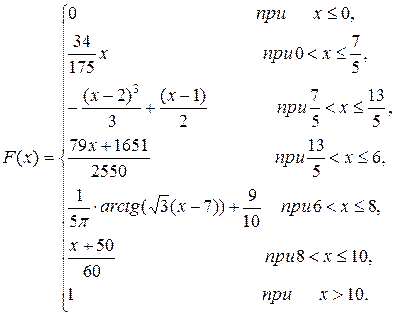
Построим графики плотности распределения (рис.13) и функции распределения (рис.14).
Вычислим математическое ожидание непрерывной случайной величины. Для этого воспользуемся формулой (14).
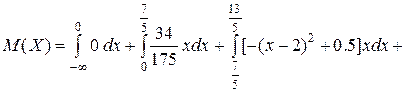
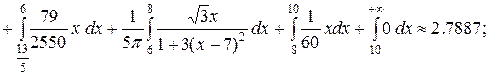
Вычислим дисперсию непрерывной случайной величины. Для этого воспользуемся формулой (21).

Рис.13
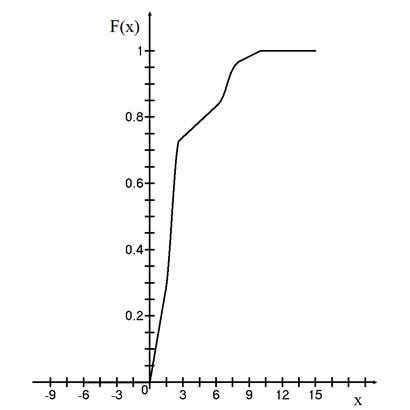
Рис.14
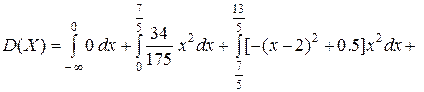
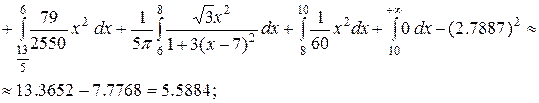
Найдём среднее квадратическое отклонение по формуле (22):
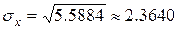
Найдём моду непрерывной случайной величины. Из рис.13 видно, что плотность распределения имеет два локальных максимума. Первый принадлежит интервалу  . Найдём производную функции, принадлежащей этому интервалу:
. Найдём производную функции, принадлежащей этому интервалу:
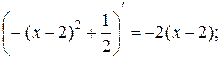
Приравниваем производную к нулю:
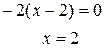
Таким образом в точке 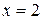 распределение имеет моду. Второй локальный максимум принадлежит интервалу
распределение имеет моду. Второй локальный максимум принадлежит интервалу 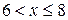 . Найдём производную функции, принадлежащей этому интервалу:
. Найдём производную функции, принадлежащей этому интервалу:
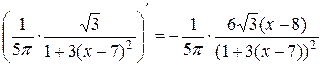 .
.
Приравниваем производную к нулю:
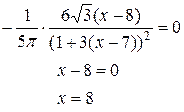
Таким образом, в точке 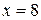 распределение также имеет моду.
распределение также имеет моду.
Запишем 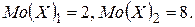
В некоторых случаях, для нахождения моды непрерывной случайной величины не нужно применять необходимое условие существования экстремума функции, то есть не нужно искать производную и приравнивать её к нулю. Это относится к тем случаям, когда максимум достигается на границе интервала кусочно-заданной функции плотности распределения.
Найдём медиану непрерывной случайной величины. Для этого воспользуемся формулой (25):
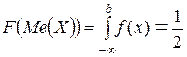
То есть необходимо вычислить интеграл, разбив его также на сумму интегралов по каждому интервалу, подставив в верхний предел последнего суммируемого интеграла неизвестную величину b. В некоторых случаях суммировать интегралы нужно не по всем интервалам, а только до среднего интервала. Это нужно для того, чтобы суммарная площадь под кривой распределения не превысила значение 0,5. Затем, вычислить интегралы и приравнять полученное выражение к 0,5, получить уравнение относительно b. Если полученное уравнение не имеет действительных решений, то необходимо изменить количество суммируемых интегралов. Поскольку рассматриваемый выше пример даёт уравнение, решение которого является трудоёмкой задачей, рассмотрим другие примеры.
Пример 1.
Пусть задана плотность распределения:
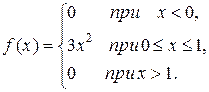
Находим медиану:
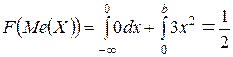
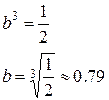
Ответ: 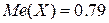 .
.
Пример 2.
Пусть задана плотность распределения:
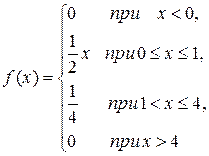
Находим медиану:
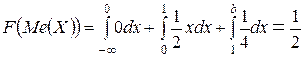 ,
,
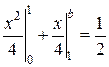 ,
,
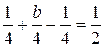 ,
,
 ,
,
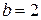 .
.
Ответ: 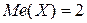 .
.
5. Содержание отчёта
Отчёт по лабораторной работе «Случайные величины» должен содержать:
─ фамилию и инициалы курсанта, номер учебной группы, название выполняемой лабораторной работы и номер варианта, указанного преподавателем;
─ ряд распределения дискретной случайной величины из варианта;
─ заполненную таблицу для расчётов математического ожидания, дисперсии, среднего квадратического отклонения;
─ вычисленную функцию распределения дискретной случайной величины;
─ график функции распределения дискретной случайной величины;
─ формулы и расчёт по ним математического ожидания, дисперсии, среднего квадратического отклонения дискретной случайной величины;
─ полигон распределения вероятностей дискретной случайной величины;
─ найденное значение моды (мод) дискретной случайной величины;
─ функцию плотности распределения непрерывной случайной величины;
─ формулы и расчёт для нахождения функции распределения непрерывной случайной величины;
─ найденную функцию распределения случайной величины;
─ графики плотности и функции распределения непрерывной случайной величины;
─ формулы и расчёт для нахождения математического ожидания, дисперсии и среднего квадратического отклонения непрерывной случайной величины;
─ описание методики нахождение моды и найденные значения моды (мод) непрерывной случайной величины;
─ описание методики нахождение медианы и найденные значения медианы непрерывной случайной величины;
─ изображение медианы на графике плотности распределениенепрерывной случайной величины.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 460; Нарушение авторских прав?; Мы поможем в написании вашей работы!