Примеры расчета центрально сжатых элементов

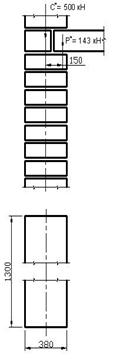
Исходные данные Рассчитать простенок третьего этажа

примера 5. пятиэтажного здания в связи с надстройкой

шестого этажа. Размеры простенка в плане и нагрузки на простенок приведены на рис.10. Высота простенка составляет Н= 3,2 м.

Простенок нагружен расчетной постоянной нагрузкой G= 500 кН и нагрузкой от междуэтажного перекрытия Р= 143 кН, приложенной с эксцентриситетом 15см.

Решение.

Толщина стены превышает 30см и поэтому влияние длительного действия нагрузки можно не учитывать - m_g =1.

Полная нагрузка на простенок

N= G+ Р= 500 + 148 = 643 кН.

Нагрузка от перекрытия создает момент относительно оси простенки

М= Р х ℮ = 143х 15 = 2140 кН.см.

Эксцентриситет приложения полной нагрузки N относительно оси простенка

M 2140 h 39

℮ _о = ---- = ------- = 3,33см<0,45 --- = 0,45 --- =

N 643 2 2

= 8,8 см.

Имеет место внецентренное сжатие с

малым эксцентриситетом.

Гибкость простенка

H 320

λ_hс = ----------- = ------ = 8,42

h –2℮_о38

Упругая характеристика кладки из керамических камней на растворе марки 25 и выше по табл.11

a= 1000.

Рис. 10. К примеру 5.

Коэффициент продольного изгиба по табл.

φ =0,9

Площадь простенка, вводимая в расчет

А= 130 х 38 = 4940 см² = 0,494 м²

Напряжения в кладке простенка

2е_о 2х 3,33

N (1+ -----) 643 (+ ---------)

h 38

σ = --------------------- = ------------------------ = 1700кПа=1,7МПа

φ х А 0,9 х 0,494

По табл.2 принимаем керамические камни марки 100 на растворе марки 75 с расчетным сопротивлением R= 1,7 МПа или камни марки 150 на растворе марки 50 с расчетным сопротивлением R= 1,8 МПа.

Несущая способность простенка

φ х R х А 0,9 х 1,7 х 10³х 0.494

N₍₁₀₀₎= --------------- = ------------------------------ = 643,4 кН≈ N= 643кН.

2е_о 2 х 3,33

1 + --------- 1+ ------------

h 38

0,9 х 1,8 х 10³х 0,494

N₍₁₅₀₎= ---------------------------- = 680,9 кН > N= 643кН.

2 х 3,33

1+ ---------------

Прочность простенка в обеих случаях обеспечена.

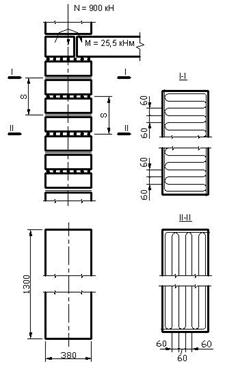
Исходные данные Рассчитать простенок первого этажа

примера 6. пятиэтажного здания в связи с

надстройкой шестого этажа. Размеры простенка и нагрузки на простенок приведены на рис.11. Высота простенка

составляет Н= 3,6м.

Простенок нагружен расчетной продольной силой G= 730 кН и нагрузкой от перекрытия 1-го этажа Р= 170 кГ, приложенной с эксцентриситетом е = 15см.

Решение.

Полная нагрузка на простенок 1-го этажа n= 730 + 170 = 900 кН.

Нагрузка от перекрытия 1-го этажа создает момент относительно оси простенка.

М= 170 х 15 = 2550 кН.см

Эксцентриситет приложения полной нагрузки N относительно оси простенка

M 2550 h 38

е_о = ---- = ------ = 2,85см<0,45 --- = 0,45 ---- =

N 900 2 2

= 8,8 см.

Имеет место случай малых

эксцентриситетов.

Гибкость простенка

H 360

λ_hс = ------- = ----- = 9,5

h 38

Упругая характеристика кладки из керамических камней на растворе марки 25 и выше по табл.

a = 1000.

Рис.11. К примеру 6

Коэффициент продольного изгиба по табл.

φ =0,885

Площадь простенка, вводимая в расчет

А= 130 х 38 = 4940 см² = 0,494 м²

Напряжения в кладке простенка

2е_о 2х 2,85

N (1+ ------) 900 (+ ---------)

h 38

σ = --------------------- = ------------------ = 2370кПа=2,37МПа

φ х А 0,885 х 0,494

Простенок сложен из керамических камней марки 150 на растворе марки 50 с расчетным сопротивлением R= 1,8 МПа.

Так как σ = 2,37 МПа >R= 1,8 МПа, то кладку простенка необходимо армировать. При гибкости простенка λ_hс = 8,42 <15 принимаем сетчатое армирование простенка из обыкновенной проволоки ВI с R_s = 180 МПа.

Определяем процент армирования μ, при котором расчетное сопротивление армированной кладки R_s.c. = 2,4 МПа ≈ σ

(σ – R) х 50 (2,4 – 1,8) х 50

μ = ---------------------- = ------------------------------- = 0,24%

4 е_о 4 х 2,85

R_s (1- ------) 180 (1- -----------)

h 38

Так как кладка армирована, необходимо внести поправку в величину упругой характеристики кладки и повторить расчет.

Упругая характеристика армированной кладки

R 1,8

a _s = a_. --------- = 1000 ------ = 750

R_s.k. 2,4

Коэффициент продольного изгиба при гибкости λ_hс = 8,42 и = 750

по табл. равен φ = 0,86

Напряжения в кладке простенка при φ = 0,86

2х 2,85

900 (+ ---------)

σ = --------------------- = 2436кПа=2,436МПа

0,86 х 0,494

Процент армирования кладки при σ= 2,436 МПа

(2,436-1,8) х 50

μ = -------------------------- = 0,253%

4 х 2,85

180 (1- ----------)

Расчетное сопротивление армированной кладки при внецентренном сжатии из кирпича марки 150 на растворе марки 50 при μ = 0,253%

2 R_s 4 е _о 2 х 180 4 х 2,85

R_s.k. = R + -------------- μ х 1- ----- = 1,8 + ------ х 0,253 (1- -----------) = 2,44МПа

100 h 100 38

Несущая способность простенка из кладки. армированной сетками

1 1

N= φ х R_s.k. х А ------------------ = 0,86 х 2,44 х (1000) х 0,494 х ------- = 901,4кН>900 кН

2 е_о 2х2,85

1+ ------- 1+------

h 38

Шаг между стержнями сетки при диаметре стержней 5мм с а_s = 0,196см² и при шаге сеток в кладке s= 22,5 см.

200 х а_s 200 х 0,196

с = ---------- = ---------------- = - 6,88 см

μ х s 0,253 х 22,5

Назначаем шаг стержней в сетке равным 6,0 см. Армирование простенка показано на рис.11

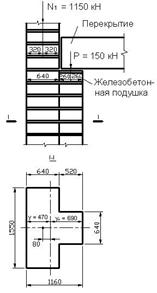
Исходные данные Подобрать марки камня и раствора для

примера 7 кирпичного простенка с пилястром

(таврового сечения) на 3-ем этаже

промышленного здания.

Высота простенка составляет 5.1 м. Нагрузки на простенок и его размеры в плане приведены на рис.12. Простенок загружен продольной силой от вышележащих этажей N₁ = 1150 кН и нагрузкой от междуэтажного перекрытия Р= 150 кН, приложенной к пилястру.

Решение

Так как толщина простенка больше 30см, то влияние длительного действия нагрузки не учитывается = m_g=1.

Определяем геометрические

характеристики простенка:

- площадь сечения.

А = А_ст + А_пил. = 155 х 64 + 64 х 52 =

=9920 + 3320 = 13240 см²

-статический момент сечения относительно грани пилястра

h_ст h_ст

S= А_ст (------- + h _пил.) + А_пил.--------------- =

2 2

64 52

= 9920 (------- + 52) + 3320--------- = 918000см³

2 2

-положение центра тяжести сечения

относительно грани пилястра

Рис. 12. К примеру 7.

S 918000

у_о= ----- = ----------- = 69 см;

А 13240

-расстояние от центра тяжести сечения до грани стены

у= d – у_о = 116 – 69 = 47 см.

Эксцентриситет приложения нагрузки относительно центра тяжести

сечения

-N₁ х е₁ + Р х е₁ - 1150+ 15 + 150 х 43

е_о = ------------------- = ---------------------------- = - 8 см,

N₁ + Р 1150 + 150

h_ст 64

где е₁ = h_пил + ------- - у_о = 52 + ---- - 69 = 15см;

2 2

h_пил 52

е₂ = у_о + ------- = 69 - ---- = 43см;

2 2

Эксцентриситет приложения нагрузки е_о = 8см < 0,45у = 0,45х47=21см. Следовательно, имеет место случай малых эксцентриситетов.

Момент инерции сечения простенка относительно центра тяжести

155х 64³ 64 64х 52³ 52

I = ---------- + 155 х 64 (47- -----)² + -------- + 64 х 52 (69- ----)² =12521408см⁴

12 2 12 2

Радиус инерции сечения простенка

I 12521408

r = √ ----- = √ ------------------ = 31 см.

А 13240

Упругая характеристика кладки на растворе марки 25 и выше по табл.

= 1000

Приведенная гибкость простенка высотой ℓ_о = Н= 5,1м

ℓ_о 510

λ_r = ------- = ----- = 16,5

r 31

Коэффициент продольного изгиба простенка по табл.

φ =0,985

Напряжения в кладке простенка

℮_о 8

N (1+ -------) (1150+150) (1+ --------)

h-у 116-47

σ = --------------------- = ------------------------------------ = 1160кПа=1,16МПа

φ х А 0,885 х 0,494

По табл. 2 принимаем кирпич марки 100 на растворе марки 25. Им соответствует кладка с расчетным сопротивлением R= 1,3 МПа > σ = 1,16 МПа.

Несущая способность простенка при принятой кладке

1 1

N=φ х R_. х А -------------- = 0,985 х 1,3 х(1000) х 1,324 х ------------ = 1519кН>1300 кН

е _о 8

(1+ ----) (1+---------)

h-у 116-47

Несущая способность простенка обеспечена.

Исходные данные Рассчитать простенок первого этажа

примера 8. промышленного здания с размерами,

приведенными в примере 7.

Нагрузки на простенок приведены на рис.13. Величины нагрузок N₁=2200кН; Р= 250кН и полная N = 2150кН.

Высота простенка Н= 6,1м.

Решение

Так как размеры сечения не изменились, то и геометрические характеристики сечения остались неизменными:

-площадь сечения А= 13240см^2;

-момент инерции I= 12521408см⁴;

-радиус инерции ч= 31см;

-положение центра тяжести сечения

у_о= 69см;

-расстояние границ стены у-47см.

эксцентриситет равнодействующей

всех сил N= 2450 кН относительно центра тяжести сечения

Рис.13. К примеру 8

-N₁ х е₁ + Р х е₂ - 2200х 15 + 250 х 43

е_о = ------------------- = ---------------------------- = 9,1 см.<

N 2450

< 0,45у = 0,45х47 = 21см.

Имеет место случай малых эксцентриситетов.

Упругая характеристика кладки = 1000

Приведенная гибкость простенка λ_ч = 16,5

Коэффициент продольного изгиба φ = 0,985

Напряжения в кладке простенка

℮_о 9,1

N (1+ ----) 2450 (1+ --------)

h-у 116-47

σ = --------------------- = ------------------------------- = 2130кПа=2,13МПа

φ х А 0,985

По табл.2 принимаем кирпич марки 100 на растворе марки 50. Этой кладке соответствует расчетное сопротивление R= 1,5МПа. Так как R< σ, то столб армируем горизонтальными прямоугольными сетками.

Необходимый процент армирования простенка при прямоугольных сетках из обыкновенной проволоки В-I с R_s = 180 МПа.

(σ – R) х 50 (2,4 – 1,8) х 50

μ = ---------------------- = --------------------- = 0,286%

2 е _о 2х 9,1

R_s (1- -------) 180 (1----------)

у 47

Так как кладка армирована, то вносим поправку в величину упругой характеристики кладки и повторяем расчет.

Упругая характеристика армированной кладки при R_s.k = 2,15Ма

R 1,5

a _s = a --------- = 1000 ------ = 700

R_s.k. 2,15

Коэффициент продольного изгиба армированной кладки при λ_ч = 16,5 и a _s.k. = 700 по табл.

φ = 0,977

Расчетное сопротивление армированной кладки при μ= 0,3%

2R_s ℮_о 2х180 2х9,1

R_s.k= R + ---------- μ (1- -----) = 1,5+ --------- х 0,3 (1- ---------)=2,16МПа

100 у 100 47

Несущая способность простенка из армированной кладки при внецентренном сжатии

1 1

N=φ х R_s.k._. х А --------- = 0,977 х 2,16х(1000) х 1,324 х ------------------- =2468,5кН>2450 кН

℮_о9,1

(1+ ----) (1+----------)

h-у 116-47

Прочность армированного простенка достаточна для восприятия действующей нагрузки.

Исходные данные Подобрать необходимые марки камня и

примера 9. раствора для простенка прямоугольного

сечения и проверить его несущую спо-

собность.

Высота простенка составляет Н= 4,2м. Размеры сечения простенка в х h = 103 х 51см. Простенок нагружен продольной силой N= 230кН и силой Р=190кН, приложенной с эксцентриситетом ℮ = 18,5см. Нагрузки на простенок приведены на рис.14.

Решение.

Площадь простенка составляет А = 103х51 = 5253см² > 3000см²

Следовательно, влияние длительного действия нагрузки можно не учитывать – m_g =1.

Изгибающий момент от действия силы Р

М= Р х ℮= 190 х 18,5 = 3515кНсм

Эксцентриситет приложения полной

нагрузки

М 3515

℮_о = ------ = ------ = 15,3 см

N 230

Имеет место случай больших

эксцентриситетов, так как

h 51

℮_о = 15,3см > 0,45 – = 0,45 х --- = 11,5см.

2 2

Принимаем упругую характеристику кладки, отвечающу марке

раствора 25 и выше (см. табл.)

a = 1000

Гибкость сжатой части простенка и коэффициент продольного изгиба

для нее

λ_п = ----- = 8, 25; φ = 0,91

Гибкость сжатой части простенка и коэффициент продольного изгиба

для нее

λ_hс = ----- = 20,6; φ_с = 0,63

20,4

h

Приведенный коэффициент продольного изгиба при ℮_о ≥ 0,45 ---- равен

φ + φ_с 0,91+0,63

φ₁ ------------- = ------------------- = 0,77

2 2

Фактические напряжения в кладке простенка

N 420

σ = --------------------------- = -------------------------------------- = 1913кПа=1,91МПа

℮_о 2х15,3

φ₁ х А √ (1+ ------) 0,77 х 0,5253 √ (1+--------)²

h 51

По табл.2 принимаем кирпич марки 150 на растворе марки 75. Им соответствует кладка с расчетным сопротивлением R= 2,0 МПа.

Несущая способность простенка

2℮_о 2х15,3

N= φ₁ х Rх А √ (1- ----)² =0,77х2,0(1000)х0,5253 √ (1- -------)² =

h 51

= 439,2 кН >420 кН.

Прочность простенка при принятых марках кирпича и раствора обеспечена.

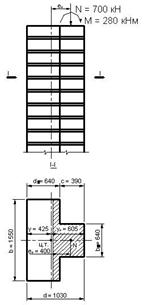
Исходные данные Подобрать марки камня и раствора для

примера 10 кирпичного простенка таврового сечения

(с пилястром) высотой 5,1м.

Нагрузки на простенок и его размеры в плане приведены на рис.15. Простенок загружен продольной силой N= 700кН и изгибающим моментом М= 280 кН.м.

Решение

Так как толщина простенка больше 30см, то влияние длительного действия нагрузки можно не учитывать –m_g =1.

Определяем геометрические характери-

стики простенка:

-площадь сечения

А= А_ст- А_пил. = 155х64+64х39= 9920+

+2496 = 12406см²;

-статический момент сечения относи-

тельно грани пилястра

h_ст h_ст

S= А_ст (----- + h _пил.) + А_пил.----- =

2 2

64 39

= 9920(---- + 39) + 2496---- = 752992см³

2 2

-положение центра тяжести сечения

относительно грани пилястра

S

Рис. 15. К примеру 10 у_о=----- = 752992/12400=60,5см;

А

-расстояние от центра тяжести сечения до грани стены

у= 64+ 39 –60,5 = 42,5 см.

Момент инерции сечения простенка относительно центра тяжести

155х 64³ 64х 39³

I = ---------- + 155 х 64 (42,5-0,5х64)² + -------- + 64 х 39 (69- 0,5х39)² =

=8675483см⁴ = 0,868 м⁴

Радиус инерции сечения простенка

r= √ I/ А = √ 8675483/ 12416 = 26,4см

Эксцентриситет приложения нагрузки относительно центра тяжести

сечения М 280

℮_о = ------- = ------ = 0,4м= 40см.

N 700

Так как ℮_о = 40см > 0,45у = 0,45 х 42,5 = 19,125см, то имеет место случай больших эксцентриситетов.

Упругая характеристика кладки = 1000

Гибкость простенка для всего сечения

ℓ_о 510

λ_r = ------- = ----- = 19,3

r 26,4

Коэффициент продольного изгиба простенка (для всего сечения)

φ =0,965

Площадь сжатой части сечения

А_с= 2(у_о- ℮_о )в_о – 2(60,5-40) х 64 = 2624см²

Гибкость сжатой части сечения

ℓ_о 510

λ_ч = ------- = ---------------- = 12,44

(у_о- ℮_о ) 2(60,5-40)

Коэффициент продольного изгиба сжатой части сечения φ_с =0,825

Приведенный коэффициент продольного изгиба

φ₁ = 0,5(φ + φ_с ) = 0,5 (0,965+0,825) = 0,895

Определяем напряжения в кладке сжатой зоны

N 420

σ = --------------------------- = -------------------------------------- = 1775кПа=1,78МПа

φ₁ х А_с √А/А_с 0,895 х 0,2624√ ---------

По табл. принимаем кирпич марки 150 на растворе марки 50. Им соответствует кладка с расчетным сопротивлением R= 1,8 МПа.

Дата добавления: 2014-10-23