К I e V

11101011 11101001 11100101 11110111

00010110010100111101010101.

§ 6. Арифметичні операції

у двійковій системі числення

Правила виконання арифметичних операцій із двійковими числами відрізняються великою простотою.

Звернемося спочатку до правила рахунка в двійковому численні:

Оскільки маємо лише дві цифри, правило переносу формулюється так: коли в який-небудь розряд, у якому стоїть 1 (сама старша цифра), додається ще одна 1, цей розряд піднімається в 0 і посилає одиницю переносу в наступний старший розряд. При безупинному додаванні одиниці в даний розряд його показання увесь час міняються на зворотні: якщо в цьому розряді стоявла 1, то вона замінюється на 0 і при цьому видається одиниця переносу.

Давайте, керуючись цими правилами, складемо самі

прості числа ID + ID:

записуємо:

+

0001

Для того щоб перевести десяткове число в двійкове, досить знати структуру коду і вагові значення розрядів. Вони зростають справа наліво у порядку зростання номерів розрядів. Їх легко запам'ятати: 1, 2, 4, 8, 16...

Користуючись цією таблицею, неважко знайти десятковий еквівалент будь-якого двійкового числа розрядністю не більш 8.

Пояснимо, як це робиться на конкретному прикладі.

Десяткове число 7 представляється сумою трьох вагових значень молодших розрядів: 4, 2, 1.

7D = 4 + 2 + 1

Відповідно до цього позначаємо одиниці в правих трьох розрядах: 7D = 111В. В всіх інших розрядах (у цьому прикладі — перед трьома одиницями) позначаємо нулі, тобто можна було записати: 7D= 00000111B. Це був би еквівалентний запис (нуль завжди нуль!). Неважко переконатися, що число 13 у двійковій формі буде мати вид 00001101.

Відзначимо, що найбільше десяткове число, яке можна представити 8-розрядним двійковим числом, 256, а 16-розрядним — 65535 (відповідно 2⁸ = 256, а 2¹⁶ = 65536). Отже, максимальний обсяг пам'яті не може перевищувати 65536 байт.

Точно так само кодуються і дробові числа. Для цього важливо враховувати, що вагові значення розрядів дробової частини числа зменшуються після коми в наступному порядку: 0,5; 0,25;

0,125 і т.д. Так, дробовому числу 7,125 відповідає двійковий код 00000111, 0010000, а числу 58,5625 — 111010,1001.

Але, як поступити, якщо десятковий дріб не кратний п'яти?

Існує правило:

Необхідно дробову частину числа помножити на 2, якщо результат по кількості знаків виходить більше дробової частини, то отриману одиницю (а виникає тільки 1) записують у розряд цілої частини (це і є двійковий код), а якщо результат по кількості знаків збігається з числом дробової частини, то на місце цілої частини ставлять нуль (це теж двійковий код).

Описаний процес необхідно продовжувати доти, поки в правій частині не одержимо чи нуль не буде досягнута необхідна точність обчислень. Підтвердимо сказане прикладами:

Приклад!. Перевести десятковий дріб 0,28125. Обчислення робимо за наступною схемою:

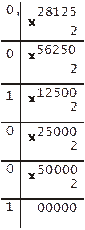
Результат: 0,28125D = 0,01001В.

Приклад 2. Перевести десятковий дріб 0.9 у двійкову систему числення.

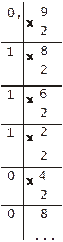
Проробіть цю операцію двома способами: використовуючи правило поділу на 2 і за допомогою таблиці вагових значень.

II. Переведіть у десятковий запис двійкові числа:

а) 101; б) 1001; в) 1100; г) 10111; д) 11011; е) 1011000;

ж) 10111011; з) 100010011; і) 1000000011;

к) 010101010101.

III. Чи можна сказати, що записані числа в двійковій

формі рівні між собою:

а) 000101101 і 101101;

б) 111011101 і 101110111;

в) 1110001101 і 01110001101;

г) 00011010,0101 і 11010,0101;

д) 11010101,01000 і 11010101,01.

IV. Двійкове число записане у виді багаточлена:

а) 1х2⁴ + 0х2³ + 1х2² + 0х2¹ + 1х2°;

б) 1х2⁶ + 1х2³ + 1х2° + 1х2^-2 + 1х2^-4;

в) 1х2⁷ + 1х2⁴ + 1х2^-3 + 1х2^-5.

Який вид має його десятковий запис?

V. Наступні двійкові числа розташуєте в порядку

зростання:

1001; 111; 100001; 010; 1101; 100; 110000; 10001.

VI. Доведіть рівність:

а) 5D = 00000101В;

б) 101111В = 47D;

в) 636D = 1001111100В;

г) 1200,875D = 10010110000,111В;

д) 01111, 125D = 10001010111, 001В.

VII. Переведіть десяткові дроби в двійкову систему

числення (відповідь запишіть із шістьма двійковими знаками):

а) 0,371D;

б) 0,7156D;

в) 0.5473D;

г) 0.8457D;

д) 0,6945В.

«И» — 11101001, буква «Е» — 11100101, буква «В» — 11110111. Таким чином, слово «КИЕВ» кодується послідовністю з 32 біт:

К И Ї В

Послідовностями нулів і одиниць можна закодувати і графічну інформацію.

У графічному середовищі Windows для IBM PC-сумісних комп'ютерів використовується так назване ANSI кодування, що відрізняється від кодування OEM для DOS-програм тим, що в ній не використовуються псевдографічні символи. Багато Windows-програм при експорті й імпорті файлів автоматично виконують перетворення з однієї системи кодування в іншу і назад.

Питання:

1. Чому двійкова система числення зручна для автоматизації?

2. Для розпізнавання чисел у різних системах числення служать покажчики. Що вони собою являють?

3. Що таке вагове значення позиції?

4. Як за допомогою «ваги» позиції двійкового числа визначити його десятковий еквівалент?

5. Приведіть правило перекладу чисел з десяткової системи числення в двійкову.

6. Яким чином перекласти дробову частину десяткового

числа в двійковий код?

7. Що позначає абревіатура ASCII?

8. Розповісти, де і навіщо застосовується алфавітний стандартний код обробки інформації.

Тренування:

I. Переведіть у двійковий запис десяткові числа:

а) 7; б) 17; в) 37; г) 48; д) 98; е) 102; ж) 193; з) 254; і) 513; к) 999.

Очевидно, що цей процес може продовжуватися нескінченно, даючи всі нові і нові знаки в зображенні двійкового еквівалента числа 0,9D. Так, за чотири кроки ми одержуємо число 0,1110В, а за сім кроків —число 0,1110011В, що є більш точним представленням числа 0,9D у двійковій системі числення, і т.д. Такий нескінченний процес обривають на деякому кроці, коли вважають, що отримано необхідну точність представлення числа.

Переклад змішаних чисел, що містять цілу і дробову частини, здійснюється в два етапи. Окремо переводиться ціла частина, окремо — дробова. У підсумковому записі отриманого числа ціла частина відокремлюється від дробової коми (крапкою).

Подібно прямому перетворенню чисел (від десяткових до двійкових) виконується і зворотне перетворення. Шукане десяткове число виходить як сума вагових значень одиничних розрядів. Наприклад: двійкове число 111010 представляється в десятковій формі по таблиці як сума ваг одиниць розрядів:

1 1 1 0 1 0

32 +16 + 8+ 0+ 2 + 0=58D

Оскільки люди в науковій і виробничій практиці користуються десятковою системою числення, то виникає задача пошуку простих правил (а точніше, алгоритмів) для перекладу чисел з десяткової системи в двійкову:

1) розділити число на 2. Зафіксувати залишок (0 або 1) і частка;

2) якщо частка не дорівнює 0, то розділити його на 2, і так далі. Якщо частка дорівнює 0, то записати всі отримані залишки, починаючи з першого, ліворуч праворуч.

Приклад:

Представити число 58D у двійковій системі числення. Розподіл здійснюється стовпчиком так, як показано нижче.

Цифрами шуканого числа, рівного даному, є усі виникаючі залишки. Поява в частці нуля означає кінець процесу розподілу:

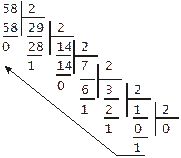
Залишки, починаючи з останнього, виписані зліва направо, утворять шукане двійкове число:

58D = 111010В

Всі операції прямого і зворотнього перетворення чисел здійснюються комп'ютером автоматично за допомогою спеціальних функціональних вузлів, зокрема регістрів, шифраторів і дешифраторів.

Основними воротами для введення інформації в комп'ютер є його клавіатура. Шляхом натискання тієї чи іншої клавіши користувач вводить у комп'ютер відповідний знак, символ» букву. Але машина в стані «сприйняти» тільки число, його двійковий код. Тому всі клавіші відповідно до їхніх позначень і положення реєстрових перемикачів з'єднані з пронумерованими електричними ланцюгами таким чином, що введення кожного символу буде рівнозначним введенню визначеного числа.

Одним з найбільш розповсюджених кодів є код ASCII (від англ. American standart code for information inter-chage — американський стандартний код для інформаційного обміну). У російському розширенні цей код одержав назву АСКИ — алфавітний код обробки інформації. Цей код (його версія КОИ-8) прийнятий як стандарт.

Кожен символ у цьому коді представляється восьмирозрядним двійковим числом (байтом). Усього існує 256 різних послідовностей з 8 нулів і одиниць — це дозволяє закодувати 256 різних символів, наприклад, великі і малі букви російського і

латинського алфавіту, цифри, розділові знаки і т.д. Відповідність байтів і символів задається за допомогою таблиці, у якій для кожного коду вказується відповідний символ. Ось фрагмент такої таблиці для кодування КОИ-8:

Таблиця 2

Код Символ	Код Символ	Код Символ	Код Символ
	110000 0	1000000 @	1010000 Р
100001!	110001 1	1000001 А	1010001 Q
100010 “	110010 2	1000010 B	1010010 R
100011 #	110011 3	1000011 С	1010011 S
100100 $	110100 4	1000100 D	1010100 Т
100101 %	110101 5	1000101 E	1010101 U
100110 &	110110 6	1000110 F	1010110 V
100111 ‘	110111 7	1000111 G	1010111 W
101000 (	111000 8	1001000 H	1011000 X
101001)	111001 9	1001001 I	1011001 Y
101010 *	111010:	1001010 J	1011010 Z
101011 +	111011;	1001011 K	1011011 [
101100,	111100 <	1001100 L	1011100 \
101101.	111101 =	1001101 M	1011101 ]
101110.	111110 >	1001110 N	1011110 ^
101111 •/	111111?	1001111 0	•••

Коду 00100000 у цій таблиці відповідає пробіл - порожній проміжок в один символ, що використовується для відділення одного слова від іншого.

Якщо, наприклад, користувач на клавіатурі набрав слово «KIEV», то, з огляду на відповідність кожної клавіші, що натискається, визначеному коду, у пам'ять комп'ютера надійде наступна послідовність двійкових чисел:

Дата добавления: 2014-10-23