Обобщенный закон Гука

Деформации при объемном напряженном состоянии.

Рассматривая вопросы прочности при объемном и плоском напряженных состояниях, необходимо в соответствии с основными гипотезами считать, что материал изотропный, следует закону Гука, а деформации малы.

Изучая центральное растяжение, сжатие, было установлено, что относительные продольная и поперечная деформации определяются выражениями

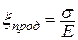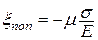, (4.12)

Эти равенства выражают закон Гука при простом растяжении или сжатии, т.е. при линейном напряженном состоянии (рис. 4.14).

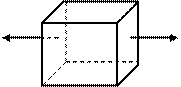Рассмотрим зависимость между напряжениями и деформациями в случае объемного напряженного состояния.

Рис.4.14

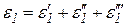Применяя принцип суперпозиции, объемное напряженное состояние изобразим как сумму трех линейных напряженных состояний (рис. 4.15). В этом случае деформацию по направлению первого главного напряжения s₁ можно записать , где 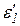, , 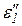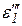- относительные удлинения в

направлении s₁, вызванные соответственно действием только

Рис. 4.15

напряжениями s₁, s₂, s₃.

Поскольку 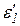является для напряжения s₁ продольной деформацией, а 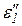, 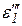- поперечными деформациями, то из формул (4.12) следует:

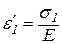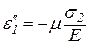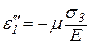, , . (4.13)

Складывая эти величины, получим .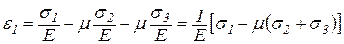

Аналогично получаются выражения для двух других главных удлинений. В результате

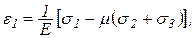
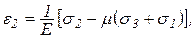(4.14)

.

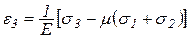Эти формулы носят название обобщенного закона Гука для изотропного тела, т. е. определяют зависимость между линейными деформациями и главными напряжениями в общем случае объемного напряженного состояния. Из этих формул легко получить закон Гука для плоского напряженного состояния. Например, :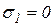

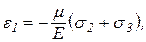
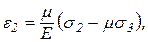
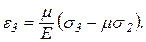
Выражения (4.14) справедливы не только для главных деформаций, но и для относительных деформаций по любым трем взаимно перпендикулярным направлениям.

При выводе аналитического выражения обобщенного закона Гука в этом случае будем

исходить из условия, что угловые деформации не зависят от нормальных напряжения, а ли-нейные деформации не зависят от касательных напряжений. В этом случае относительное удлинение по направлению оси х будет обусловлено напряжением σ_х и равно 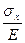. Напряжениям 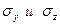в этом направлении будут соответствовать удлинения 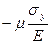и 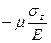.По аналогии получим такие же выражения для 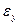и .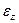

Таким образом,

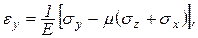(4.15)

.

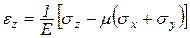Угловые деформации определяются соответствующими касательными напряжениями

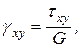
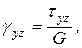
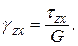(4.16)

Совокупность деформаций, возникающих по различн ым направлениям и в различных плоскостях, проходящих через данную точку, называется деформированным состоянием в точке.

Наряду с линейной и угловой деформацией в сопротивлении материалов приходится рассматривать иногда и объёмную деформацию, т.е., относительное изменение объема в точке. Линейные размеры ребер элементарного параллелепипеда 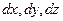в результате деформации меняются и становятся равными 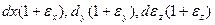. Абсолютное приращение объёма определится разностью

-.

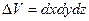
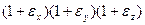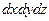Раскрывая скобки и пренебрегая произведениями линейных деформаций, как величинами второго порядка малости, получим .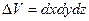

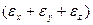Относительное изменение объёма обозначается буквой е и определится из отношения

е.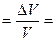

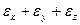Заменив деформации их выражениями по закону Гука, получим

e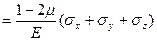 (4.17)

Это соотношение на ряду с формулами (4.14)-(4.16) относится к обобщенному закону Гука.

4.8 П отенциальная энергия деформации

Дата добавления: 2014-10-23