Момент очередного отсчета определяется выполнением равенства 2 страница

Кроме того, так как мера неопределенности связывается нами только с фактом выбора, а не с множеством конкретных значений наблюдаемых явлений, то Н(р₁ … ρ_N) должна быть функцией от функции распределения случайной величины и не должна зависеть от ее конкретных значений. Иначе говоря, Η(ρ₁...ρ_N) должна являться функционалом распределения вероятностей.

Еще одно условие состоит в том, что мера неопределенности не должна зависеть от пути выбора состояния в ансамбле. Выбор может быть как непосредственным, так и многоступенчатым. В последнем случае неопределенность выбора состояния складывается из неопределенности выбора группы состояний и неопределенностей выбора состояния в каждой группе, рассчитанных с учетом вероятности выбора данной группы:

где q₁, q₂ и q₃, q₄ — вероятности состояний, образующих соответственно группы Ν—1 и Ν, причем ρ_N-1 = q₁ + q₂ и p_N-1 = q₃ + q₄.

Мера неопределенности выбора дискретным источником состояния из ансамбля U, удовлетворяющая указанным условиям, была предложена американским ученым К. Шенноном [36]. Ее называют энтропией дискретного источника информации или энтропией конечного ансамбля:

где С — произвольное положительное число.

К. Шенноном высказано утверждение, а советским ученым Л. Я- Хинчиным математически строго доказано, что это единственный функционал, удовлетворяющий сформулированным условиям.

Если снова ориентироваться на измерение неопределенности в двоичных единицах, то основание логарифма следует принять равным двум. Примем также С= 1. Из (3.5)

Предложенная мера была названа энтропией не случайно. Дело в том, что формальная структура выражения (3.5) совпадает с энтропией физической системы, определенной ранее Больцманом. Согласно второму закону термодинамики энтропия H замкнутого пространства определяется выражением

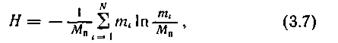
где M_n — число молекул в данном пространстве; m_i — число молекул, обладающих скоростью u_I + Du.

Так как m_i/М_п есть вероятность того, что молекула имеет скорость u_i + Δu, то (3.7) можем записать в виде

Совпадение имеет глубокий физический смысл, так как в обоих случаях величина H характеризует степень разнообразия состояний системы.

Рассмотрим взаимосвязь меры К. Шеннона с мерой Хартли. Если в источнике может быть реализовано N равновероятных состояний, то вероятность каждого из них равна р_i = (1/N)(1iN) и неопределенность, по Хартли, приходящаяся на каждое состояние, выражается числом

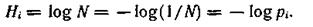
Будем теперь считать вероятности событий различными, а неопределенность, приходящуюся на одно конкретное состояние источника, характеризовать по аналогии величиной

Эта частная неопределенность представляет собой случайную величину, зависящую от того, какое состояние источника в действительности реализуется. Усреднив по всему ансамблю U состояний источника, найдем неопределенность, приходящуюся в среднем на одно состояние:

Следовательно, мера К. Шеннона является естественным обобщением меры Хартли на случай ансамбля с неравновероятными состояниями. Она позволяет учесть статистические свойства источника информации.

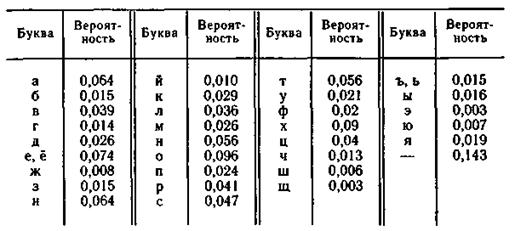
Пример 3.2. Сравнить неопределенность, приходящуюся на букву источника информации u (алфавита русского языка), характеризуемого ансамблем, представленным в табл. 3.1, с неопределенностью, которая была бы у того же источника при равновероятном использовании букв.

Таблица 3.1

При одинаковых вероятностях появления всех 32 букв алфавита неопределенность, приходящаяся на одну букву, составляет

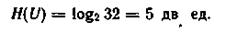
Энтропию источника, характеризуемого заданным ансамблем (табл. 3.1), находим, используя формулу (3.6):

Таким образом, неравномерность распределения вероятностей использования букв снижает энтропию источника с 5 до 4.42 дв. ед.

§ 3.2 СВОЙСТВА ЭНТРОПИИ

Рассмотрим основные свойства энтропии, обратив внимание на то, что сформулированные условия для меры неопределенности выполняются.

1. Энтропия является вещественной и неотрицательной величиной, так как для любого i(1) р_i изменяется в интервале от 0 до 1, log p_i отрицателен и, следовательно, — p_i log p_i положительна.

2. Энтропия — величина ограниченная. Для слагаемых - p_i log p_i в диапазоне 0<р_i1 ограниченность очевидна. Остается определить предел, к которому стремится слагаемое — p_i log p_i, при р_i—>0, поскольку — log p_i при этом неограниченно возрастает:

Обозначив a= 1/р_i и воспользовавшись правилом Лопиталя, получим

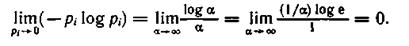
3. Энтропия обращается в нуль лишь в том случае, если вероятность одного из состояний равна единице; тогда вероятности всех остальных состояний, естественно, равны нулю. Это положение соответствует случаю, когда состояние источника полностью определено.

4. Энтропия максимальна, когда все состояния источника равновероятны, что легко доказывается методом неопределенных множителей Лагранжа [23]:

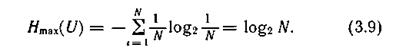
5. Энтропия источника и с двумя состояниями u₁ и u₂ изменяется от нуля до единицы, достигая максимума при равенстве их вероятностей:

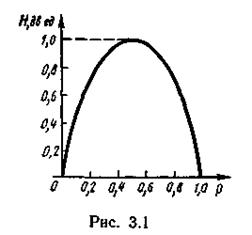
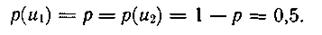
График зависимости H(U) в функции ρ

приведен на рис. 3.1. При ρ «(1- р)частная неопределенность, приходящаяся на состояние u₁, велика, однако такие состояния источника весьма редки. Состояния u₂ реализуются часто, но неопределенность, приходящаяся на такое состояние, очень мала. Поэтому энтропия, характеризующая среднюю неопределенность на одно состояние ансамбля, также мала. Аналогичная ситуация наблюдается при р» (1—р)·

Отметим, что энтропия непрерывно зависит от вероятностей отдельных состояний, что непосредственно вытекает из непрерывности функции - p log p.

6. Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропии исходных источников.

Не теряя общности, ограничимся рассмотрением объединения, включающего два источника информации u и u. Под объединением двух источников u и u понимают обобщенный источник информации (u,u), характеризующийся вероятностями p(u_iu_i) всех возможных комбинаций состояний u_i, источника u и u_i, источника u. Аналогично трактуется и объединение ансамблей.

В соответствии с определением энтропия объединения

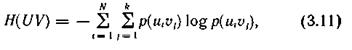
здесь p(u_iu_i) — вероятности совместной реализации состояний

В случае статистической независимости источников информации u и υ запишем

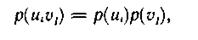
тогда

Учитывая, что

получим

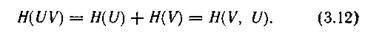
Соответственно для энтропии объединения нескольких независимых источников u, u, z имеем

В дальнейшем для придания общности получаемым результатам о неопределенности выбора будем говорить в основном применительно к математическим моделям источников информации в виде ансамблей.

7. Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля. При ее определении используют только вероятности состояний, полностью игнорируя их содержательную сторону. Поэтому энтропия не может служить средством решения любых задач, связанных с неопределенностью. Например, при использовании этой меры для оценки неопределенности действия лекарства, приводящего к полному выздоровлению больных в 90 % случаев и улучшению самочувствия в остальных 10 % случаев, она получится такой же, как и у лекарства, вызывающего в 90 % случаев смерть, а в 10 % — ухудшение состояния больных.

8. Энтропия как мера неопределенности согласуется с экспериментальными данными, полученными при изучении психологических реакций человека, в частности реакции выбора. Установлено, что время безошибочной реакции на последовательность беспорядочно чередующихся равновероятных раздражителей (например, загорающихся лампочек) растет с увеличением их числа так же, как энтропия. Это время характеризует неопределенность выбора одного раздражителя.

Замена равновероятных раздражителей неравновероятными приводит к снижению среднего времени реакции ровно настолько, насколько уменьшается энтропия.

Пример 3.3. Заданы ансамбли U и V двух дискретных случайных величин U' и V¢:

Сравнить их энтропии.

Так как энтропия не зависит от конкретных значений случайной величины, а вероятности их появления у обеих величин одинаковы, то

§ 3.3. УСЛОВНАЯ ЭНТРОПИЯ И ЕЕ СВОЙСТВА

При оценке неопределенности выбора часто необходимо учитывать статистические связи, которые в большинстве случаев имеют место как между состояниями двух или нескольких источников, объединенных в рамках одной системы, так и между состояниями, последовательно выбираемыми одним источником.

Определим энтропию объединения двух статистически связанных ансамблей U и V. Объединение ансамблей характеризуется матрицей p(UV) вероятностей р(u_iu_i) всех возможных комбинаций состояний u_i(1£ i £ N) ансамбля U и состояний u_j(1 £ j £ k) ансамбля V:

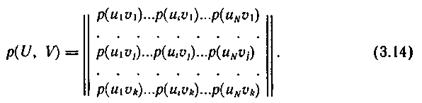
Суммируя столбцы и строки матрицы (3.14), получим информацию об ансамблях U и V исходных источников u и u:

Вероятности р(u_iu_i) совместной реализации взаимозависимых состояний и, и ν·, можно выразить через условные вероятности р(u_i/u_i) или p(u_j/u_i) в соответствии с тем, какие состояния принять за причину, а какие — за следствие:

где p(u_i/u_j) — вероятность реализации состояний u_i ансамбля U при условии, что реализовалось состояние u_j ансамбля V; P(u_j/u_i) — вероятность реализации состояния u_j ансамбля V при условии, что реализовалось состояние u_i ансамбля U. Тогда выражение (3.11) для энтропии объединения принимает вид

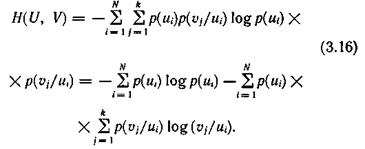
Сумма

представляет собой случайную величину, характеризующую неопределенность, приходящуюся на одно состояние ансамбля V при условии, что реализовалось конкретное состояние u_i ансамбля U.

Назовем ее частной условной энтропией ансамбля V и обозначим H_ui(V):

При усреднении по всем состояниям ансамбля U получаем среднюю неопределенность, приходящуюся на одно состояние ансамбля V при известных состояниях ансамбля U:

или

Величину Н_U(V) называют полной условной или просто условной энтропией ансамбля V по отношению к ансамблю U.

Подставляя (3.19) в (3.16), получаем

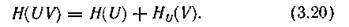
Выражая в (3.11) p(u_iu_j) через другую условную вероятность в соответствии с (3.15), найдем

где

и

Таким образом, энтропия объединения двух статистически связанных ансамблей U и V равна безусловной энтропии одного ансамбля плюс условная энтропия другого относительно первого.

Распространяя правило (3.19) на объединение любого числа зависимых ансамблей, получим

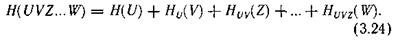
Покажем теперь, что в объединении ансамблей условная энтропия любого ансамбля всегда меньше или равна безусловной энтропии того же ансамбля.

Для объединения двух ансамблей U и V данное утверждение принимает вид соотношений

Из (3.20) и (3.25) следует, что объединение двух произвольных ансамблей удовлетворяет соотношению

Для объединения нескольких произвольных ансамблей соответственно имеем

Действительно, наличие сведений о результатах реализации состояний одного ансамбля никак не может увеличить неопределенность выбора состояния из другого ансамбля. Эта неопределенность может только уменьшиться, если существует взаимосвязь в реализациях состояний из обоих ансамблей.

В случае отсутствия статистической связи в реализациях состояний u_i, из ансамбля U и υ_j из ансамбля V сведения о результатах выбора состояний из одного ансамбля не снижают неопределенности выбора состояний из другого ансамбля, что находит отражение в равенствах

Если имеет место однозначная связь в реализациях состояний u_i(1 £ i £ N) из ансамбля U и u_j(1 £ j £ N) из ансамбля V, то условная энтропия любого из ансамблей равна нулю:

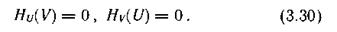
Действительно, условные вероятности р(u_i/u_j) и P(u_j/u_i) в этом случае принимают значения, равные нулю или единице. Поэтому все слагаемые, входящие в выражения (3.17) и (3.23) для частных условных энтропии, равны нулю. Тогда в соответствии с (3.18) и (3.22) условные энтропии также равны нулю.

Равенства (3.30) отражают факт отсутствия дополнительной неопределенности при выборе событий из второго ансамбля.

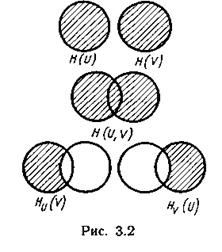
Уяснению соотношений между рассмотренными энтропиями дискретных источников информации (ансамблей) способствует их графическое отображение (рис. 3.2).

Пример 3.4. Определить энтропии Н(U), H(V), Η_u(U), H(UV), если задана матрица вероятностей состояний системы, объединяющей источники u и u:

Вычисляем безусловные вероятности состояний каждой системы как суммы совместных вероятностей по строкам и столбцам заданной матрицы:

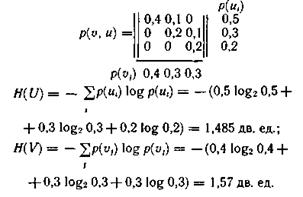
Определяем условные вероятности

Пример 3.5. Известны энтропии двух зависимых источников: H(U) = 5 дв. ед., H(V) = 10 дв. ед. Определить, в каких пределах будет изменяться условная энтропия Ηυ(V) при изменении H_V(U) в максимально возможных пределах.

При решении удобно использовать графическое отображение связи между этропиями. Из рис. 3.3. видим, что максимального значения Hu(V) достигает при отсутствии взаимосвязи и будет равно H(V), т.е. 10 дв. ед. По мере увеличения взаимосвязи Н_u(V) будет уменьшаться до значения H(V) — H(U) = 5 дв. ед. При этом H_V(U) = 0.

§ 3.4. ЭНТРОПИЯ НЕПРЕРЫВНОГО ИСТОЧНИКА ИНФОРМАЦИИ (ДИФФЕРЕНЦИАЛЬНАЯ ЭНТРОПИЯ)

В предыдущих параграфах была рассмотрена мера неопределенности выбора для дискретного источника информации. На практике мы в основном встречаемся с источниками информации, множество возможных состояний которых составляет континуум. Такие источники называют непрерывными источниками информации.

Во многих случаях они преобразуются в дискретные посредством использования устройств дискретизации и квантования. Вместе с тем существует немало и таких систем, в которых информация передается и преобразуется непосредственно в форме непрерывных сигналов. Примерами могут служить системы телефонной связи и телевидения.

Оценка неопределенности выбора для непрерывного источника информации имеет определенную специфику. Во-первых, значения, реализуемые источником, математически отображаются непрерывной случайной величиной. Во-вторых, вероятности значений этой случайной величины не могут использоваться для оценки неопределенности, поскольку в данном случае вероятность любого конкретного значения равна нулю.

Естественно, однако, связывать неопределенность выбора значения непрерывной случайной величины с плотностью распределения вероятностей этих значений. Учитывая, что для совокупности значений, относящихся к любому сколь угодно малому интервалу непрерывной случайной величины, вероятность конечна, попытаемся найти формулу для энтропии непрерывного источника информации, используя операции квантования и последующего предельного перехода при уменьшении кванта до нуля.

С этой целью разобьем диапазон изменения непрерывной случайной величины U, характеризующейся плотностью распределения вероятностей р(u), на конечное число n малых интервалов шириной Δu (рис. 3.4). При реализации любого значения u, принадлежащего интервалу (), будем считать, что реализовалось значение дискретной случайной величины U. Поскольку Δu мало, вероятность реализации значения u из интервала :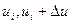

Тогда энтропия дискретной случайной величины Ữ может быть записана в виде:

или

Так как

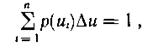
то

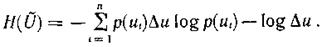
По мере уменьшения Δu 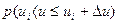все больше приближается к вероятности , равной нулю, а свойства дискретной величины Ữ — к свойствам непрерывной случайной величины U.

Переходя к пределу при Δu→0, получаем следующее выражение для энтропии H(U) непрерывного источника:

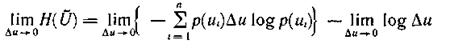
или

Эта величина при Δu→0 стремится к бесконечности, что полностью соответствует интуитивному представлению о том, что неопределенность выбора из бесконечно большого числа возможных состояний (значений) бесконечно велика.

Первый член в правой части соотношения (3.31) имеет конечное значение, которое зависит только от закона распределения непрерывной случайной величины U и не зависит от шага квантования Δu. Он имеет точно такую же структуру, как энтропия дискретного источника.

Второй член того же соотношения, наоборот, зависит лишь от шага квантования случайной величины U. Именно в нем кроется причина того, что величина H(U) обращается в бесконечность.

К использованию и трактовке соотношения (3.31) для получения конечной характеристики информационных свойств непрерывного источника известны два подхода.

Один подход состоит в том, что в качестве меры неопределенности непрерывного источника принимают первый член соотношения (3.31):

Поскольку для определения этой величины используется только функция плотности вероятности, т. е. дифференциальный закон распределения, она получила название относительной дифференциальной энтропии или просто дифференциальной энтропии непрерывного источника информации (непрерывного распределения случайной величины U).

Ее можно трактовать как среднюю неопределенность выбора случайной величины U с произвольным законом распределения по сравнению со средней неопределенностью выбора случайной величины U', изменяющейся в диапазоне, равном единице, и имеющей равномерное распределение.

Действительно, запишем соотношение (3.31) для случайной величины U', равномерно распределенной в интервале δ:

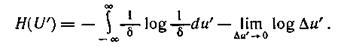
При δ=1

откуда при Δu=Δu'

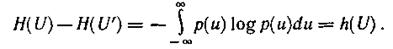
Аналогично, используя операции квантования и предельного перехода, найдем выражение для условной энтропии непрерывного источника информации:

Отметим, что второй член в первой части выражения (3.33) идентичен соответствующему члену в соотношении (3.31). Обозначим первый член правой части выражения (3.33) через h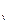(U):

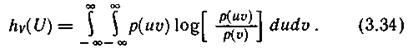
Эта величина конечна и называется относительной дифференциальной условной энтропией или просто дифференциальной условной энтропией непрерывного источника. Она характеризует неопределенность выбора непрерывной случайной величины U при условии, что известны результаты реализации значений другой статистически связанной с ней непрерывной случайной величины V, и по сравнению со средней неопределенностью выбора случайной величины U', изменяющейся в диапазоне, равном единице, и имеющей равномерное распределение вероятностей.

При втором подходе к использованию соотношения (3.31) для количественного определения информационных свойств непрерывного источника информации предлагается принять во внимание практическую невозможность обеспечения бесконечно высокой точности различения определенных значений непрерывной величины U. Поэтому все бесконечное число значений U в пределах заданной точности измерений следует рассматривать как одно значение.

Из средней неопределенности выбора источником u некоторого значения в этом случае необходимо вычесть среднюю неопределенность того же источника, полученную при условии, что мы знаем результаты определения U с некоторой определенной точностью ε. Тогда информационные свойства непрерывного источника будут оцениваться разностью безусловной и условной энтропий, определяемых соотношениями (3.31) и (3.33) соответственно. Такая разность, как будет показано в § 3.5, является мерой снятой неопределенности, называемой количеством информации.

Таким образом, при втором подходе безусловная и условная энтропии непрерывного источника рассматриваются лишь как некоторые вспомогательные величины, с помощью которых можно определить количество информации. Соотношение между понятиями энтропии и количества информации для непрерывного источника информации подобно соотношению между потенциалом, определенным с привлечением понятия бесконечности, и напряжением, определенным как разность потенциалов.

Поскольку вторые члены в правых частях соотношений (3.31) и (3.33) одинаковы, разность безусловной и условной энтропий непрерывного источника информации равна разности дифференциальных безусловной и условной энтропий того же источника, причем относительность их уже несущественна, так как разность не зависит от стандарта, с которым они сравнивались.

§ 3.5. СВОЙСТВА ДИФФЕРЕНЦИАЛЬНОЙ ЭНТРОПИИ

1. Дифференциальная энтропия в отличие от энтропии дискретного источника является относительной мерой неопределенности. Ее значение зависит от масштаба случайной величины U, а следовательно, и от выбора единицы ее измерения.

Изменим масштаб случайной величины U, например, в k раз, оставив неизменным масштаб равномерно распределенной в единичном интервале случайной величины U', принятой за эталон. Если 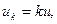то .

Тогда

Если одновременно изменить масштаб величины U', то относительная неопределенность также изменится, так как значение эталона будет уже иным.

Из относительности дифференциальной энтропии следует, что энтропия может принимать положительные, отрицательные и нулевые значения.

2. Дифференциальная энтропия не зависит от конкретных значений случайной величины U и, в частности, от изменения всех ее значений на постоянное. Действительно, масштаб U при этом не меняется и справедливо равенство

3. Какие же непрерывные распределения обладают максимальной дифференциальной энтропией?

а. Если единственным ограничением для случайной величины U является область ее возможных значений [α, β], то максимальной дифференциальной энтропией обладает равномерное распределение вероятностей в этой области.

При доказательстве решается задача определения плотности распределения р(u), обеспечивающей максимальное значение функционала

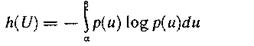
при ограничении

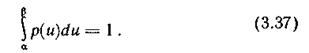
Используя, например, метод неопределенных множителей Лагранжа, получим

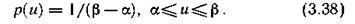
Нетрудно убедиться в том, что найденная функция р(u) обеспечивает максимум функционала h(U), причем

б. Если ограничения на область значений непрерывной случайной величины U отсутствуют, но известно, что дисперсия ее ограничена, то максимальной дифференциальной энтропией обладает нормальное распределение величины U.

Дата добавления: 2014-10-23