Момент очередного отсчета определяется выполнением равенства 3 страница

При доказательстве решается задача определения функции р(u), обеспечивающей максимальное значение функционала

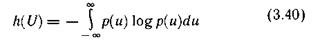
при ограничениях

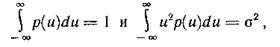
где σ — среднеквадратическое отклонение от математического ожидания Ū =0 (σ — заданное ограничение).

Искомую плотность распределения р(u) находят, например, методом неопределенных множителей Лагранжа.

Она оказывается гауссовской:

Вычислив функционал (3.40) для этого распределения, получим значение максимальной дифференциальной энтропии 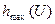. В двоичных единицах неопределенности

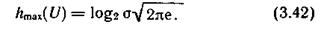
Поскольку в информационных системах сигнал, описываемый случайной величиной U, часто представляет собой электрическое напряжение (или ток), дисперсия U пропорциональна средней мощности сигнала. Тогда в соответствии с (3.41) можно утверждать, что при заданной мощности наибольшей средней неопределенностью выбора будет обладать источник, генерирующий сигналы, амплитуды которых распределены по нормальному закону.

4. Соотношения для дифференциальной энтропии объединения статистически зависимых непрерывных источников аналогичны соответствующим формулам для дискретных источников:

где

Справедливость соотношения (3.43) легко проверить подстановкой выражения (3.32), заданного для h(V), и выражения (3.34) —для .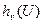

Так как

то

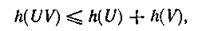
причем равенство имеет место только в случае отсутствия статистической связи между U и V.

Пример 3.6. Определить, насколько мы выиграем в мощности, используя для организации мешающего воздействия, характеризующегося энтропией, источник шума с гауссовской плотностью распределения по сравнению с источником, имеющим в интервале [α, β] равномерную плотность распределения.

В соответствии с (3.42) дифференциальная энтропия гауссовского распределения

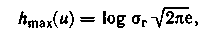
где σ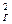— дисперсия, характеризующая мощность, выделяемую на резисторе с сопротивлением в 1 Ом.

Для равномерного распределения энтропия определена соотношением (3.39):

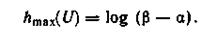
Вычислим дисперсию σравномерного на интервале [α, β] распределения:

Из условия обеспечения равенства энтропий следует

Возведя (3.46) в квадрат и подставив в (3.44), получим

Следовательно, искомый выигрыш составляет 42 %.

§ 3.6. КОЛИЧЕСТВО ИНФОРМАЦИИ КАК МЕРА СНЯТОЙ НЕОПРЕДЕЛЕННОСТИ

Передача информации инициируется либо самим источником информации, либо осуществляется по запросу. Она диктуется желанием устранить неопределенность относительно последовательности состояний, реализуемых некоторым источником информации. Обычно запрос обусловлен отсутствием возможности наблюдать состояния источника непосредственно. Поэтому абонент обращается к информационной системе, которая извлекает интересующую его информацию из источника посредством некоторого первичного преобразователя и направляет ее по каналу связи абоненту.

Информация проявляется всегда в форме сигналов. Сигналы z, поступающие с выхода первичного преобразователя источника информации на вход канала связи, принято называть сообщениями в отличие от сигнала u, формирующихся на входе линии связи. В зависимости от формы создаваемых сообщений различают источники дискретных и непрерывных сообщений.

Отдельные первичные сигналы с выхода источника дискретных сообщений называют элементами сообщения. Каждому элементу сообщения соответствует определенное состояние источника информации. В случае параллельной реализации источником информации множества состояний, как это имеет место, например, в документах с печатным текстом, первичный преобразователь, в частности, обеспечивает их последовательное отображение элементами сообщения. Таким преобразователем может быть как автоматическое читающее устройство, так и человек.

Основное понятие теории информации — количество информации — рассматривается в данном параграфе применительно к передаче отдельных статистически несвязанных элементов сообщения. Дискретный источник сообщений при этом полностью характеризуется ансамблем

а непрерывный — одномерной плотностью распределения случайной величины — z — ρ(z). Особенности определения количества информации при передаче сообщений изложены в § 4.2.

Передача информации от дискретного источника. Выясним, насколько будет изменяться неопределенность относительно состояния источника сообщения при получении адресатом элемента сообщения с выхода канала связи. Алфавиты передаваемых и принимаемых элементов сообщения считаем идентичными.

Вследствие воздействия помех полученный элемент сообщения в общем случае отличается от переданного. Подчеркнем это различие. Обозначив принимаемые элементы сообщения другими буквами: .

Априорная неопределенность (неопределенность до получения элемента сообщения) относительно состояния источника не является полной. Предполагается, что адресату известен алфавит элементов сообщения, а из прошлого опыта он знает вероятности их появления. Считая, что состояния источника реализуются независимо, априорная частная неопределенность появления элемента сообщения

где — априорная вероятность появления элемента сообщения .

Предполагаются также известными некоторые сведения относительно помехи в канале связи. Обычно считают, что между элементами сообщения и помехой статистические связи отсутствуют, искажения отдельных элементов сообщения являются событиями независимыми и адресату известна совокупность условных вероятностей 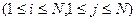того, что вместо элемента сообщения , будет принят элемент сообщения .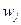

При получении конкретного элемента сообщения 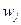, адресату становится известным значение условной вероятности , называемой апостериорной (послеопытной) вероятностью реализации источником элемента сообщения . Это позволяет найти апостериорную частную неопределенность, остающуюся у адресата относительно выдачи источников элемента сообщения после получения конкретного элемента сообщения :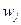

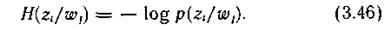
Поскольку получение информации мы связываем с уменьшением неопределенности, естественно определить частное количество информации , получаемое при приеме элемента сообщения 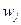относительно некоторого реализованного источником элемента сообщения как разность частных неопределенностей, имевшихся у адресата до и после получения элемента сообщения (априорной и апостериорной):

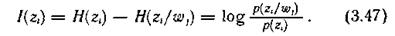
Анализ формулы (3.47) позволяет сделать следующие заключения:

1) частное количество информации растет с уменьшением априорной и увеличением апостериорной вероятностей реализации элемента сообщения источником, что находится в полном соответствии с нашими интуитивными представлениями;

2) частное количество информации об элементе сообщения может быть не только положительным, но и отрицательным, а также нулем, что зависит от соотношения априорной и апостериорной вероятностей. Если вероятность того, что источником был реализован элемент сообщения увеличилась после приема элемента сообщения 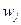, т. е. >, то полученное частное количество информации положительно. Если эта вероятность не изменилась, т. е. =, то имевшая место неопределенность тоже не изменилась и частное количество информации равно нулю.

Наконец, случай <соответствует увеличению неопределенности относительно реализации после получения элемента сообщения 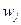, и, следовательно, частное количество информации отрицательно;

3) в случае отсутствия помехи апостериорная вероятность = 1. При этом частное количество информации численно совпадает с частной априорной неопределенностью реализации данного элемента сообщения :

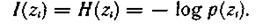
Это максимальное частное количество информации, которое можно получить об элементе сообщения ;

4) частное количество информации относительно реализации источником элемента сообщения , содержащееся в принятом элементе сообщения 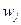, равно частному количеству информации относительно 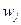, содержащемуся в элементе сообщения :

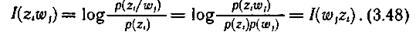
Хотя имеют место случаи, где важно оценить частное количество информации , для задач анализа и оптимизации функционирования информационных систем более рациональны усредненные характеристики, отражающие статистические свойства источника информации и канала связи.

Найдем среднее количество информации, содержащееся в любом принятом элементе сообщения относительно переданного (реализованного) источником. До получения конкретного элемента сообщения средняя неопределенность, имеющаяся у адресата, относительно реализации источником любого элемента сообщения равна энтропии источника. Ее называют априорной энтропией источника.

Средняя неопределенность относительно любого состояния источника, остающаяся у адресата после получения конкретного элемента сообщения 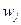, характеризуется частной условной энтропией :

Это случайная величина, зависящая от того, какой конкретно элемент сообщения принят.

Средняя неопределенность по всему ансамблю принимаемых элементов сообщений равна условной энтропии источника :

или

Эту условную энтропию называют апостериорной энтропией источника информации.

Таким образом, при наличии помех среднее количество информации, содержащееся в каждом принятом элементе сообщения, относительно любого переданного равно разности априорной и апостериорной энтропии источника:

Представив априорную и апостериорную энтропии соответственно выражениями (3.6) и (3.50) и проведя несложные преобразования, получим формулу для количества информации непосредственно через вероятности:

Если частный характер количества информации специально не оговаривается, мы всегда имеем дело с количеством информации, приходящимся в среднем на один элемент сообщения. Поэтому указание об усреднении опускается.

Передача информации от непрерывного источника. Количество информации, получаемой от непрерывного источника по каналу с помехами, определяется так же, как в случае, рассмотренном выше, но с использованием понятия дифференциальной энтропии.

Для источника, имеющего непрерывное множество состояний, среднее количество информации, содержащееся в каждом принятом значении случайной величины относительно переданного значения случайной величины Ζ, можно получить как разность априорной и апостериорной дифференциальных энтропий:

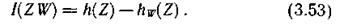
Соотношение (3.53) несложно выразить в виде, подобном (3.52):

Относительность дифференциальных энтропий в этом случае не принимается во внимание, поскольку количество информации не зависит от выбранного стандарта сравнения.

Основные свойства количества информации. 1. Несмотря на то, что частное количество информации может быть величиной отрицательной, количество информации неотрицательно.

Действительно, согласно выражению

Тогда

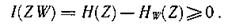
2. При отсутствии статистической связи между случайными величинами Ζ и W

следовательно, в этом случае

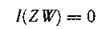
(принятые элементы сообщения не несут никакой информации относительно переданных).

3. Количество информации в W относительно Ζ равно количеству информации в Ζ относительно W.

Для доказательства этого утверждения воспользуемся выражением

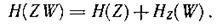
Аналогично можно записать

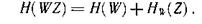
Так как

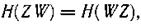
то

откуда

4. При взаимно однозначном соответствии между множествами передаваемых и принимаемых элементов сообщений, что имеет место в отсутствии помехи, апостериорная энтропия равна нулю и количество информации численно совпадает с энтропией источника:

Это максимальное количество информации о состоянии дискретного источника. Для непрерывного источника оно равно бесконечности.

Пример 3.7. Выстрел из орудия не поражает цель с вероятностью р. Через какое число выстрелов следует поинтересоваться у разведчика-корректировщика, уничтожена ли цель, чтобы в результате ответа получить максимальное количество информации?

Ансамбль интересующих нас событий включает: — цель поражена; — цель не поражена. Вероятность того, что цель не поражена после k выстрелов, равна . Вероятность противоположного события (1—). Поскольку после ответа корректировщика неопределенность устраняется полностью, количество информации равно энтропии, а она максимальна при равновероятности событий. Следовательно,

откуда

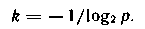
Пример 3.8. Определить среднее количество информации, получаемое при передаче элемента сообщения по каналу, описанному матрицей совместных вероятностей передачи и приема элементов сообщения

Безусловные вероятности посылаемых z и принимаемых w элементов сообщения определены при рассмотрении примера 3 4. Там же получены значения для априорной H(Z) и апостериорной энтропий.

В соответствии с (3.51)

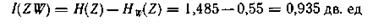
§ 3.7. ЭПСИЛОН-ЭНТРОПИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Ранее было показано, что неопределенность реализации непрерывным источником информации состояния в конкретный момент времени (отсчета) равна бесконечности. Тем более равна бесконечности неопределенность реализации непрерывным источником конкретного сигнала длительности Т.

Однако такой результат получен в предположении возможности фиксировать любые сколь угодно малые различия между реализациями. На практике такая возможность отсутствует. Это объясняется тем, что воспринимающие информацию датчики, включая человека, обладают ограниченной чувствительностью и конечной разрешающей способностью, а также тем, что процесс восприятия сопровождается помехами.

Если учесть, что нас интересует приближенное восприятие реализации, то количество информации, приходящееся на отсчет или на единицу времени, можно вычислить.

Ограничимся рассмотрением простейшего случая, когда отдельные состояния источника информации представляют собой независимые реализации случайной величины U. (Эпсилон - энтропия случайного процесса рассмотрена в § 4.4.)

Ансамбль реализаций случайной величины U описывается плотностью распределения вероятностей р(u). О значениях случайной величины U можно судить по значениям другой случайной величины Ζ, если мера их различия не превышает заданной верности воспроизведения. В этом случае говорят, что Ζ воспроизводит U.

Для количественной оценки степени сходства сигналов целесообразно ввести какую-либо функцию ρ(z, u), имеющую природу «расстояния». Тогда удобным критерием верности V(Z, U) является среднее значение функции p(z, u), взятое по всему множеству значений z и u:

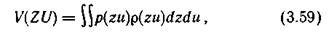
где ρ(z, u) — плотность совместного распределения вероятностей величин Ζ и U.

Наиболее широко используется среднеквадратический критерий, при котором ρ(z, u) представляет собой квадрат обычного евклидова расстояния между точками в соответствующем пространстве (см. § 2.12).

Требование к верности в данном случае задается с использованием критерия V(ZU):

где 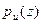— условная плотность распределения — функция правдоподобия того, что конкретный сигнал u будет воспроизведен как сигнал z; ε — заданное значение верности.

Так как плотность р(u) определена, то для выполнения условия (3.60) варьировать можно только условной плотностью распределения .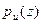

Если случайная величина Ζ воспроизводит случайную величину U с некоторой верностью ε, то количество информации, содержащееся в воспроизводящей величине Ζ относительно U, конечно и в соответствии с (3.54) может быть записано в форме

где

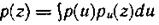
- плотность воспроизводящей величины Ζ.

Желательно обеспечить заданную верность воспроизведения при минимальном количестве получаемой информации. Поэтому среди множества функций 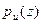, удовлетворяющих условию (3.60), целесообразно выбрать такую, которая обеспечивает наименьшее I(ZU) [10, 35].

Минимальное количество информации в одной случайной величине Ζ относительно другой U, при котором удовлетворяется заданное требование к верности воспроизведения величины U, называется ε-энтропией величины U и обозначается :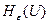

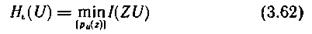
при

Используя безусловную и условную дифференциальные энтропии величины U, выражение (3.63) можно представить в виде

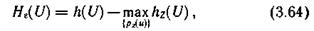
где — условная плотность вероятности того, что в тех случаях, когда был принят сигнал z, передавался сигнал u.

Пример 3.9. Найти 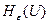источника информации, ансамбль состояний которого описывается нормально распределенной случайной величиной U с дисперсией 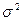при верности воспроизведения .

Будем считать, что заданная верность воспроизведения обусловлена действием аддитивной статистически не связанной с сигналом помехой Ξ, причем Μ [Ξ] =0 и Μ[Ξ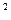] = ε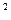. Передаваемый сигнал u рассматриваем как сумму воспроизводящего сигнала z и помехи u=z+.

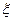Так как в данном случае в выражении (3.64) полностью определяется помехой

то

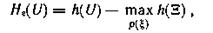
где h(Ξ) — дифференциальная энтропия помехи; ρ(ξ) — плотность распределения помехи Ξ.

Ранее [см. (3.41)] нами установлено, что при ограничении на дисперсию случайной величины максимальной дифференциальной энтропией обладает нормальное распределение. Поэтому в соответствии с (3.42) получаем

откуда

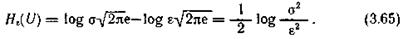
Так как σ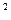определяет среднюю мощность Рсигнала, а ε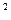— среднюю мощность ρпомехи Ξ, то выражение (3.65) характеризует зависимость эпсилон - энтропии от величины , называемой отношением сигнал/помеха.

При заданном отношении сигнал/помеха значение H(U) для нормально распределенной случайной величины является максимально возможным.

Для произвольно распределенной случайной величины U при том же критерии верности и малых ε [когда H(U) велико] справедливо приближенное равенство

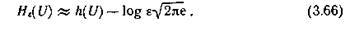
Контрольные вопросы

1. В чем сущность требования аддитивности к мере неопределенности выбора?

2. Назовите основной недостаток меры неопределенности, предложенной Хартли.

3. В каких единицах измеряется неопределенность выбора?

4. Какие требования предъявляются к мере неопределенности выбора из дискретного ансамбля?

5. Охарактеризуйте сущность понятия энтропии.

6. Изложите основные свойства энтропии дискретного ансамбля.

7. Запишите выражение для условной энтропии и поясните ее смысл.

8. Как определить энтропию нескольких взаимозависимых ансамблей?

9. Какова особенность определения энтропии непрерывного источника информации?

10. Дайте определение дифференциальной энтропии и сформулируйте ее основные свойства.

11. Какие распределения обладают максимальной дифференциальной энтропией:

а) при ограничении на диапазон изменения случайной величины?

б) при ограничении на дисперсию случайной величины?

12. Как связаны между собой понятия количества информации и энтропии?

13. Чем различаются понятия частного и среднего количества информации?

14. Сформулируйте основные свойства количества информации.

15. Запишите выражения для определения количества информации при неполной достоверности передачи:

а) от дискретного источника;

б) от непрерывного источника.

16. В чем сущность эпсилон - энтропии случайной величины?

17. Охарактеризуйте среднеквадратический критерий верности воспроизведения.

18. Покажите, что при среднеквадратическом критерии верности воспроизведения эпсилон - энтропия максимальна для нормально распределенной случайной величины с ограниченной дисперсией.

ГЛАВА 4. ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ ИСТОЧНИКА СООБЩЕНИЙ И КАНАЛА СВЯЗИ

§ 4.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Опираясь на формализованное описание сигналов и введенную меру количества информации, рассмотрим информационные характеристики источников сообщений и каналов связи, позволяющие установить пути повышения эффективности систем передачи информации, и, в частности, определить условия, при которых можно достигнуть максимальной скорости передачи сообщений по каналу связи как в отсутствие, так и при наличии помех.

Дата добавления: 2014-10-23