Момент очередного отсчета определяется выполнением равенства 10 страница

Элемент В, естественно, содержится в этом смежном классе, так как любая подгруппа содержит нулевой элемент. Взяв последовательно некоторые элементы В_j группы, не вошедшие в уже образованные смежные классы, можно разложить всю группу на смежные классы по подгруппе А.

Элементы B_j называют образующими элементами смежных классов подгруппы.

В таблице разложения, иногда называемой групповой таблицей, образующие элементы обычно располагают в крайнем левом столбце, причем крайним левым элементом подгруппы является нулевой элемент.

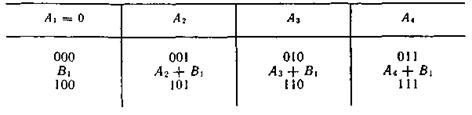
Пример 6.3. Разложим группу трехразрядных двоичных кодовых комбинаций по подгруппе двухразрядных кодовых комбинаций.

Разложение выполняем в соответствии с табл. 6.2.

Таблица 6.2

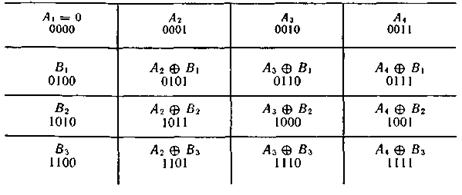
Пример 6.4. Разложим группу четырехразрядных двоичных кодовых комбинаций по подгруппе двухразрядных кодовых комбинаций.

Существует много вариантов разложения в зависимости от того, какие элементы выбраны в качестве образующих смежных классов. Один из вариантов представлен в табл. 6.3.

Таблица 6.3

Кольцом называют множество элементов R, на котором определены две операции (сложения и умножения), такие, что:

1) множество R является коммутативной группой по сложению;

2) произведение элементов aR и bR есть элемент R (замкнутость по отношению к умножению);

3) для любых трех элементов а, b и с из R справедливо равенство a(bc) = (ab)c (ассоциативный закон для умножения);

4) для любых трех элементов а, b и с из R выполняются соотношения а(b+с) = =ab+ас и (b+c)a = bа+са (дистрибутивные законы).

Если для любых двух элементов кольца справедливо соотношение ab = bа, кольцо называют коммутативным. Кольцо может не иметь единичного элемента по умножению и обратных элементов.

Примером кольца может служить множество действительных четных целых чисел относительно обычных операций сложения и умножения.

Полем F называют множество по крайней мере двух элементов, в котором определены две операции — сложение и умножение, и выполняются следующие аксиомы:

1) множество элементов образует коммутативную группу по сложению;

2) множество ненулевых элементов образует коммутативную группу по умножению;

3) для любых трех элементов множества а, b, с выполняется соотношение (дистрибутивный закон)

Поле F является, следовательно, коммутативным кольцом с единичным элементом по умножению, в котором каждый ненулевой элемент обладает обратным элементом. Примером поля может служить множество всех действительных чисел.

Поле GF(P), состоящее из конечного числа элементов Р, называют конечным полем или полем Галуа. Для любого числа Р, являющегося степенью простого числа q, существует поле, насчитывающее Р элементов. Например, совокупность чисел по модулю q, если q — простое число, является полем.

Поле не может содержать менее двух элементов, поскольку в нем должны быть по крайней мере единичный элемент относительно операции сложения (0) и единичный элемент относительно операции умножения (1). Поле, включающее только 0 и 1, обозначим GF (2). Правила сложения и умножения в поле с двумя элементами следующие:

Двоичные кодовые комбинации, являющиеся упорядоченными последовательностями из n элементов поля GF (2), рассматриваются в теории кодирования как частный случай последовательностей из n элементов поля GF(P). Такой подход позволяет строить и анализировать коды с основанием, равным степени простого числа.

В общем случае суммой кодовых комбинаций A_j, и A_i называют комбинацию A_f = A_i+A_j, в которой любой символ A_k (k=1, 2,..., n) представляет собой сумму k-x символов исходных комбинаций, причем суммирование производится по правилам поля GF(P). При этом вся совокупность n-разрядных кодовых комбинаций оказывается абелевой группой.

В частном случае, когда основанием кода является простое число q, правило сложения в поле GF(q) совпадает с правилом сложения по заданному модулю q.

Линейный код как подпространство линейного векторного пространства. В рассмотренных алгебраических системах (группа, кольцо, поле) операции относились к одному классу математических объектов (элементов). Такие операции называют внутренними законами композиции элементов.

В теории кодирования широко используются модели, охватывающие два класса математических объектов (например, L и Ω). Помимо внутренних законов композиции в них задаются внешние законы композиции элементов, по которым любым элементам ωΩ и a L ставится в соответствие элемент cL.

Линейным векторным пространством над полем элементов F (скаляров) называют множество элементов V (векторов), если для него выполняются следующие аксиомы:

1) множество V является коммутативной группой относительно операции сложения;

2) для любого вектора ν из V и любого скаляра с из F определено произведение с v, которое содержится в V (замкнутость по отношению умножения на скаляр);

3) если u и ν из V векторы, а с и d из F скаляры, то справедливо (дистрибутивные законы);

4) если ν — вектор, а с и d — скаляры, то (cd)v = c(dv) и 1 · ν = ν (ассоциативный закон для умножения на скаляр).

Выше было определено правило поразрядного сложения кодовых комбинаций, при котором вся их совокупность образует абелеву группу. Определим теперь операцию умножения последовательности из n элементов поля GF(P) (кодовой комбинации) на элемент поля а _i из GF(P) аналогично правилу умножения вектора на скаляр:

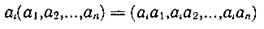
[умножение элементов производится по правилам поля GF(P)].

Поскольку при выбранных операциях дистрибутивные законы и ассоциативный закон (п. 3, 4) выполняются, все множество n-разрядных кодовых комбинаций можно рассматривать как векторное линейное пространство над полем GF(P), а кодовые комбинации — как его векторы.

В частности, при двоичном кодировании векторы состоят из элементов поля GF (2) (т. е. 0 и 1). Сложение проводят поразрядно по модулю 2. При умножении вектора на один элемент поля (1) он не изменяется, а умножение на другой (0) превращает его в единичный элемент векторного пространства, обозначаемый символом 0= (0 0...0).

Если в линейном пространстве последовательностей из n элементов поля GF(P) дополнительно задать операцию умножения векторов, удовлетворяющую определенным условиям (ассоциативности, замкнутости, билинейности по отношению к умножению на скаляры), то вся совокупность n-разрядных кодовых комбинаций превращается в линейную коммутативную алгебру над полем коэффициентов GF(P).

Подмножество элементов векторного пространства, которое удовлетворяет аксиомам векторного пространства, называют подпространством.

Линейным кодом называют множество векторов, образующих подпространство векторного пространства всех n-разрядных кодовых комбинаций над полем GF(P).

В случае двоичного кодирования такого подпространствo комбинаций над полем GF (2) образует любая совокупность двоичных кодовых комбинаций, являющаяся подгруппой группы всех n-разрядных двоичных кодовых комбинаций. Поэтому любой двоичный линейный код является групповым.

§ 6.4. ПОСТРОЕНИЕ ДВОИЧНОГО ГРУППОВОГО КОДА

Построение конкретного корректирующего кода производят, исходя из требуемого объема кода Q, т. е. необходимого числа передаваемых команд или дискретных значений измеряемой величины и статистических данных о наиболее вероятных векторах ошибок в используемом канале связи. Вектором ошибки называют n-разрядную двоичную последовательность, имеющую единицы в разрядах, подвергшихся искажению, и нули во всех остальных разрядах. Любую искаженную кодовую комбинацию можно рассматривать теперь как сумму (или разность) по модулю 2 исходной разрешенной кодовой комбинации и вектора ошибки.

Исходя из неравенства (нулевая комбинация часто не используется, так как не меняет состояния канала связи), определяем число информационных разрядов k, необходимое для передачи заданного числа команд обычным двоичным кодом.

Каждой из 2^k-1 ненулевых комбинаций k-разрядного безызбыточного кода нам необходимо поставить в соответствие комбинацию из n символов. Значения символов в n — k проверочных разрядах такой комбинации устанавливаются в результате суммирования по модулю 2 значений символов в определенных информационных разрядах.

Поскольку множество 2^k комбинаций информационных символов (включая нулевую) образует подгруппу группы всех n-разрядных комбинаций, то и множество 2^k n-разрядных комбинаций, полученных по указанному правилу, тоже является подгруппой группы n-разрядных кодовых комбинаций. Это множество разрешенных кодовых комбинаций и будет групповым кодом.

Нам надлежит определить число проверочных разрядов и номера информационных разрядов, входящих в каждое из равенств для определения символов в проверочных разрядах.

Разложим группу 2ⁿ всех n-разрядных комбинаций на смежные классы по подгруппе 2^k разрешенных n-разрядных кодовых комбинаций, проверочные разряды в которых еще не заполнены. Помимо самой подгруппы кода в разложении насчитывается 2^n-k —1 смежных классов. Элементы каждого класса представляют собой суммы по модулю 2 комбинаций кода и образующих элементов данного класса. Если за образующие элементы каждого класса принять те наиболее вероятные для заданного канала связи вектора ошибок, которые должны быть исправлены, то в каждом смежном классе сгруппируются кодовые комбинации, получающиеся в результате воздействия на все разрешенные комбинации определенного вектора ошибки. Для исправления любой полученной на выходе канала связи кодовой комбинации теперь достаточно определить, к какому классу смежности она относится. Складывая ее затем (по модулю 2) с образующим элементом этого смежного класса, получаем истинную комбинацию кода.

Ясно, что из общего числа возможных ошибок групповой код может исправить всего разновидностей ошибок по числу смежных классов.

Чтобы иметь возможность получить информацию о том, к какому смежному классу относится полученная комбинация, каждому смежному классу должна быть поставлена в соответствие некоторая контрольная последовательность символов, называемая опознавателем (синдромом).

Каждый символ опознавателя определяют в результате проверки на приемной стороне справедливости одного из равенств, которые мы составим для определения значений проверочных символов при кодировании.

Ранее указывалось, что в двоичном линейном коде значения проверочных символов подбирают так, чтобы сумма по модулю 2 всех символов (включая проверочный), входящих в каждое из равенств, равнялась нулю. В таком случае число единиц среди этих символов четное. Поэтому операции определения символов опознавателя называют проверками на четность. При отсутствии ошибок в результате всех проверок на четность образуется опознаватель, состоящий из одних нулей. Если проверочное равенство не удовлетворяется, то в соответствующем разряде опознавателя появляется единица. Исправление ошибок возможно лишь при наличии взаимно однозначного соответствия между множеством опознавателей и множеством смежных классов, а следовательно, и множеством подлежащих исправлению векторов ошибок.

Таким образом, количество подлежащих исправлению ошибок является определяющим для выбора числа избыточных символов n — k. Их должно быть достаточно для того, чтобы обеспечить необходимое число опознавателей.

Если, например, необходимо исправить все одиночные независимые ошибки, то исправлению подлежат n ошибок:

Различных ненулевых опознавателей должно быть не менее n. Необходимое число проверочных разрядов, следовательно, должно определяться из соотношения

или

Если необходимо исправить не только все единичные, но и все двойные независимые ошибки, соответствующее неравенство принимает вид

В общем случае для исправления всех независимых ошибок кратности до s включительно получаем

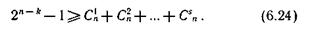
Стоит подчеркнуть, что в приведенных соотношениях указывается теоретический предел минимально возможного числа проверочных символов, который далеко не во всех случаях можно реализовать практически. Часто проверочных символов требуется больше, чем следует из соответствующего равенства.

Одна из причин этого выяснится при рассмотрении процесса сопоставления каждой подлежащей исправлению ошибки с ее опознавателем.

Составление таблицы опознавателей. Начнем для простоты с установления опознавателей для случая исправления одиночных ошибок. Допустим, что необходимо закодировать 15 команд. Тогда требуемое число информационных разрядов равно четырем. Пользуясь соотношением 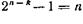, определяем общее число разрядов кода, а следовательно, и число ошибок, подлежащих исправлению (n = 7). Три избыточных разряда позволяют использовать в качестве опознавателей трехразрядные двоичные последовательности.

В данном случае ненулевые последовательности в принципе могут быть сопоставлены с подлежащими исправлению ошибками в любом порядке. Однако более целесообразно сопоставлять их с ошибками в разрядах, начиная с младшего, в порядке возрастания двоичных чисел (табл. 6.4).

Таблица 6.4

При таком сопоставлении каждый опознаватель представляет собой двоичное число, указывающее номер разряда, в котором произошла ошибка.

Коды, в которых опознаватели устанавливаются по указанному принципу, известны как коды Хэмминга.

Возьмем теперь более сложный случай исправления одиночных и двойных независимых ошибок. В качестве опознавателей одиночных ошибок в первом и втором разрядах можно принять, как и ранее, комбинации 0...001 и 0...010.

Однако в качестве опознавателя одиночной ошибки в третьем разряде комбинацию 0...011 взять нельзя. Такая комбинация соответствует ошибке одновременно в первом и во втором разрядах, а она также подлежит исправлению и, следовательно, ей должен соответствовать свой опознаватель 0...011.

В качестве опознавателя одиночной ошибки в третьем разряде можно взять только трехразрядную комбинацию 0...0100, так как множество двухразрядных комбинаций уже исчерпано. Подлежащий исправлению вектор ошибки 0...0101 также можно рассматривать как результат суммарного воздействия двух векторов ошибок 0...0100 и 0...001 и, следовательно, ему должен быть поставлен в соответствие опознаватель, представляющий собой сумму по модулю 2 опознавателей этих ошибок, т.е. 0...0101.

Аналогично находим, что опознавателем вектора ошибки 0...0110 является комбинация 0...0110.

Определяя опознаватель для одиночной ошибки в четвертом разряде, замечаем, что еще не использована одна из трехразрядных комбинаций, а именно 0...0111. Однако, выбирая в качестве опознавателя единичной ошибки в i -м разряде комбинацию с числом разрядов, меньшим i, необходимо убедиться в том, что для всех остальных подлежащих исправлению векторов ошибок, имеющих единицы в ί-м и более младших разрядах, получатся опознаватели, отличные от уже использованных. В нашем случае подлежащими исправлению векторами ошибок с единицами в четвертом и более младших разрядах являются:

0...01001, 0...01010, 0...01100.

Если одиночной ошибке в четвертом разряде поставить в соответствие опознаватель 0...0111, то для указанных векторов опознавателями должны были бы быть соответственно

Однако эти комбинации уже использованы в качестве опознавателей других векторов ошибок, а именно: 0...0110, 0...0101, 0...0011.

Следовательно, во избежание неоднозначности при декодировании в качестве опознавателя одиночной ошибки в четвертом разряде следует взять четырехразрядную комбинацию 1000. Тогда для векторов ошибок 0...01001, 0...01010, 0...01100 опознавателями соответственно будут: 0...01001, 0...01010, 0...01100.

Аналогично можно установить, что в качестве опознавателя одиночной ошибки в пятом разряде может быть выбрана не использованная ранее четырехразрядная комбинация 01111.

Действительно, для всех остальных подлежащих исправлению векторов ошибок с единицей в пятом и более младших разрядах получаем опознаватели, отличающиеся οт ранее установленных:

Векторы ошибок Опознаватели

0 010001 0 0110

0 010010 0 01101

0 010100 0 01011

0 011000 0 00111

Продолжая сопоставление, можно получить таблицу опознавателей для векторов ошибок данного типа с любым числом разрядов. Так как опознаватели векторов ошибок с единицами в нескольких разрядах устанавливаются как суммы по модулю 2 опознавателей одиночных ошибок в этих разрядах, то для определения правил Построения кода и составления проверочных равенств Достаточно знать только опознаватели одиночных ошибок в каждом из разрядов. Для построения кодов, исправляющих двойные независимые ошибки, таблица таких опознавателей определена [27] с помощью вычислительной машины вплоть до 29-го разряда. Опознаватели одиночных ошибок в первых пятнадцати разрядах приведены в табл. 6.5.

Таблица 6.5

По тому же принципу аналогичные таблицы определены и для ошибок других типов, например для тройных независимых ошибок, пачек ошибок в два и три символа.

Определение проверочных равенств. Итак, для любого кода, имеющего целью исправлять наиболее вероятные векторы ошибок заданного канала связи (взаимно независимые ошибки или пачки ошибок), можно составить таблицу опознавателей одиночных ошибок в каждом из разрядов. Пользуясь этой таблицей, нетрудно определить, символы каких разрядов должны входить в каждую из проверок на четность.

Рассмотрим в качестве примера опознаватели для кодов предназначенных исправлять единичные ошибки (табл. 6.6).

Таблица 6.6

В принципе можно построить код, усекая эту таблицу на любом уровне. Однако из таблицы видно, что оптимальными будут коды (7, 4), (15, 11), где первое число равно n, а второе k, и другие, которые среди кодов, имеющих одно и то же число проверочных символов, допускают наибольшее число информационных символов.

Усечем эту таблицу на седьмом разряде и найдем номера разрядов, символы которых должны войти в каждое из проверочных равенств.

Предположим, что в результате первой проверки на четность для младшего разряда опознавателя будет получена единица. Очевидно, это может быть следствием ошибки в одном из разрядов, опознаватели которых в младшем разряде имеют единицу. Следовательно, первое проверочное равенство должно включать символы 1, 3, 5 и 7-го разрядов;

Единица во втором разряде опознавателя может быть следствием ошибки в разрядах, опознаватели которых имеют единицу во втором разряде. Отсюда второе проверочное равенство должно иметь вид

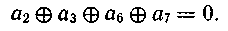
Аналогично находим и третье равенство:

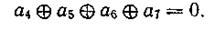
Чтобы эти равенства при отсутствии ошибок удовлетворялись для любых значений информационных символов в кодовой комбинации, в нашем распоряжении имеется три проверочных разряда. Мы должны так выбрать номера этих разрядов, чтобы каждый из них входил только в одно из равенств. Это обеспечит однозначное определение значений символов в проверочных разрядах при кодировании. Указанному условию удовлетворяют разряды, опознаватели которых имеют по одной единице. В нашем случае это будут первый, второй и четвертый разряды.

Таким образом, для кода (7, 4), исправляющего одиночные ошибки, искомые правила построения кода, т. е. соотношения, реализуемые в процессе кодирования, принимают вид:

Поскольку построенный код имеет минимальное хэммингово расстояние d_min = =3, он в соответствии с (6.15) может использоваться с целью обнаружения единичных и двойных ошибок. Обращаясь к табл. 6.6, легко убедиться, что сумма любых двух опознавателей единичных ошибок дает ненулевой опознаватель, что и является признаком наличия ошибки.

Пример 6.5. Построим групповой код объемом 15 слов, способный исправлять единичные и обнаруживать двойные ошибки.

В соответствии с (6.17) код должен обладать минимальным хэмминговым расстоянием, равным 4. Такой код можно построить в два этапа. Сначала строим код заданного объема, способный исправлять единичные ошибки. Это код Хэмминга (7, 4). Затем добавляем еще один проверочный разряд, который обеспечивает четность числа единиц в разрешенных комбинациях.

Таким образом, получаем код (8, 4). В процессе кодирования реализуются соотношения:

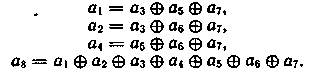
Обозначив синдром кода (7, 4) через S_i, результат общей проверки на четности через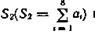

и пренебрегая возможностью

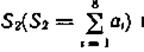
возникновения ошибок кратности 3 и выше, запишем алгоритм декодирования:

при S₁ = 0 и S₂ = 0 ошибок нет;

при S₁=0 и S₂ = 1 ошибка в восьмом разряде;

при S₁=0 и S₂ = 0 двойная ошибка (коррекция блокируется, посылается запрос повторной передачи),

при S₁=0 и S₂=1 одиночная ошибка (осуществляется ее исправление).

Пример 6.6. Используя табл. 6.6, составим правила построения кода (8,2), исправляющего все одиночные и двойные ошибки.

Усекая табл. 6.5 на восьмом разряде, найдем следующие проверочные равенства:

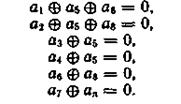
Соответственно правила построения кода выразим соотношениями

Отметим, что для построенного кода d_min=5, и, следовательно, он может использоваться обнаружения ошибок кратности от 1 до 4.

Соотношения, отражающие процессы кодирования и декодирования двоичных линейных кодов, могут быть реализованы непосредственно с использованием сумматоров по модулю два. Однако декодирующие устройства, построенные таким путем для кодов, предназначенных исправлять многократные ошибки, чрезвычайно громоздки. В этом случае более эффективны другие принципы декодирования.

Мажоритарное декодирование групповых кодов. Для линейных кодов, рассчитанных на исправление многократных ошибок, часто более простыми оказываются декодирующие устройства, построенные по мажоритарному принципу. Это метод декодирования называют также принципом голосования или способом декодирования по большинству проверок. В настоящее время известно значительное число кодов, допускающих мажоритарную схему декодирования, а также сформулированы некоторые подходы при конструировании таких кодов.

Мажоритарное декодирование тоже базируется на системе проверочных равенств. Система последовательно может быть разрешена относительно каждой из независимых переменных, причем в силу избыточности это можно сделать не единственным способом.

Любой символ a_i, выражается d (минимальное кодовое расстояние) различными независимыми способами в виде линейных комбинаций других символов. При этом может использоваться тривиальная проверка а_i = а_i. Результаты вычислений подаются на соответствующий этому символу мажоритарный элемент. Последний представляет собой схему, имеющую d входов и один выход, на котором появляется единица, когда возбуждается больше половины его входов, и нуль, когда возбуждается число таких входов меньше половины. Если ошибки отсутствуют, то проверочные равенства не нарушаются, и на выходе мажоритарного элемента получаем истинное значение символа. Если число проверок d^2s+1 и появление ошибки кратности s и менее не приводит к нарушению более s проверок, то правильное решение может быть принято по большинству неискаженных проверок. Чтобы указанное условие выполнялось, любой другой символ a_j(j неравно i) не должен входить более чем в одно проверочное равенство. В этом случае мы имеем дело с системой разделенных проверок.

Пример 6.7. Построим систему разделенных проверок для декодирования информационных символов рассмотренного ранее группового кода (8,2).

Поскольку код рассчитан на исправление любых единичных и двойных ошибок, число проверочных равенств для определения каждого символа должно быть не менее 5. Подставив в равенства (6.26 а) и (6.26 б) значения a₈, полученные из равенств (6.26д) и (6.26е), и записав их относительно а₅ совместно с равенствами (6.26 в) и (6.26г) и тривиальным равенством a₅ = a₅, получим следующую систему разделенных проверок для символа а₅:

Для символа а₈ систему разделенных проверок строим аналогично

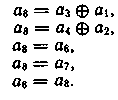
Матричное представление линейных кодов. Матрицей размерности lxn называют упорядоченное множество lxn элементов, расположенных в виде прямоугольной таблицы с l строками и n столбцами:

Транспонированной матрицей к матрице А называют матрицу, строками которой являются столбцы, а столбцами строки матрицы А:

Матрицу размерности nxn называют квадратной матрицей порядка n. Квадратную матрицу, у которой по одной из диагоналей расположены только единицы, а все остальные элементы равны нулю, называют единичной матрицей I. Суммой двух матриц А = |а_ij| и В = |b_ij| размерности lxn называют матрицу размерности lxn:

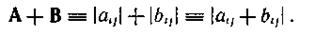
Умножение матрицы Α = |а_ij| размерности lxn на скаляр с дает матрицу размерности lxn:

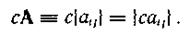
Матрицы А == |а_ij| размерности lxn и В = |b_ij| размерности nxm могут быть перемножены, причем элементами C_ik матрицы — произведения размерности lxm являются суммы произведений элементов l-й строки матрицы А на соответствующие элементы k-ro столбца матрицы В:

В теории кодирования элементами матрицы являются элементы некоторого поля GF(P), а строки и столбцы матрицы рассматриваются как векторы. Сложение и умножение элементов матриц осуществляется по правилам поля GF(P).

Пример 6.8. Вычислим произведение матриц с элементами из поля GF(2):

Элементы C_ik матрицы произведения М=М₁М₂ будут равны:

Следовательно,

Дата добавления: 2014-10-23