Момент очередного отсчета определяется выполнением равенства 12 страница

Полученный циклический код с проверкой на четность способен обнаруживать не только одиночные ошибки в отдельных разрядах, но и ошибки в любом нечетном числе разрядов.

Исправление одиночных или обнаружение двойных ошибок. Прежде чем исправить одиночную ошибку в принятой комбинации из n разрядов, необходимо определить, какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенном разряде соответствуют свой класс вычетов и свой опознаватель. Так как в циклическом коде опознавателями ошибок являются остатки от деления многочленов ошибок на образующий многочлен кода g(x), то g(x) должно обеспечить требуемое число различных остатков при делении векторов ошибок с единицей в искаженном разряде. Как отмечалось, наибольшее число остатков дает неприводимый многочлен. При степени многочлена m = n — k он может дать 2^n-k-1 ненулевых остатков (нулевой остаток является опознавателем безошибочной передачи).

Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравенства

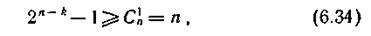
где С_n — общее число разновидностей одиночных ошибок в кодовой комбинации из n символов; отсюда находим степень образующего многочлена кода

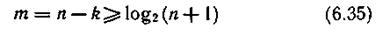
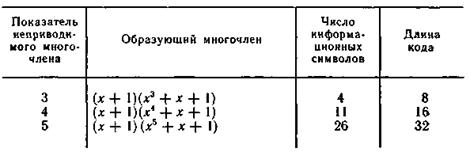
и общее число символов в кодовой комбинации. Наибольшие значения k и n для различных m можно найти, пользуясь табл. 6.11.

Как указывалось, образующий многочлен g(x) должен быть делителем двучлена хⁿ⁺¹. Доказано [20], что любой двучлен типа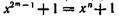может быть представлен произведением всех неприводимых многочленов, степени которых являются делителями числа m (от 1 до m включительно). Следовательно, для любого m существует по крайней мере один неприводимый многочлен степени m, входящий сомножителем в разложение двучлена хⁿ⁺¹.

Таблица 6.11

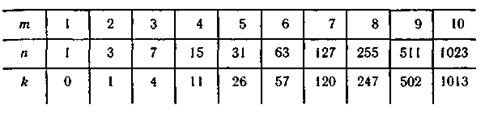
Пользуясь этим свойством, а также имеющимися в ряде книг [20] таблицами многочленов, неприводимых при двоичных коэффициентах, выбрать образующий многочлен при известных n и m несложно. Определив образующий многочлен, необходимо убедиться в том, что он обеспечивает заданное число остатков.

Пример 6.13. Выберем образующий многочлен для случая n = 15 и m = 4.

Двучлен x¹⁵+1 можно записать в виде произведения всех неприводимых многочленов, степени которых являются делителями числа 4. Последнее делится на 1, 2, 4.

В таблице неприводимых многочленов находим один многочлен первой степени, а именно х+1, один многочлен второй степени х² + х+1 и три многочлена четвертой степени: х⁴ + x + 1, х⁴ + х³+1, х⁴ + х³+х + 1. Перемножив все многочлены, убедимся в справедливости соотношения (х+1)(х² + х + 1)(х⁴ + х+1)(х⁴ + х³+ l)(x⁴ + x³ + +x²+x+1) = x¹²+1.

Один из сомножителей четвертой степени может быть принят за образующий многочлен кода. Возьмем, например, многочлен х⁴ + х³ + 1, или в виде двоичной последовательности 11001.

Чтобы убедиться, что каждому вектору ошибки соответствует отличный от других остаток, необходимо поделить каждый из этих векторов на 11001.

Векторы ошибок т младших разрядов имеют вид:

00...0001, 00...0010, 00...0100, 00...1000.

Степени соответствующих им многочленов меньше степени образующего многочлена g(x). Поэтому они сами являются остатками при нулевой целой части. Остаток, соответствующий вектору ошибки в следующем старшем разряде, получаем при делении 00...10000 на 11001, т.е.

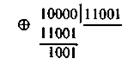
Аналогично могут быть найдены и остальные остатки. Однако их можно получить проще, деля на g(x) комбинацию в виде единицы с рядом нулей и выписывая все промежуточные остатки:

При последующем делении остатки повторяются.

Таким образом, мы убедились в том, что число различных остатков при выбранном g(x) равно n = 15, и, следовательно, код, образованный таким g(x), способен исправить любую одиночную ошибку С тем же успехом за образующий многочлен кода мог быть принят и многочлен х⁴+x+1. При этом был бы получен код, эквивалентный выбранному.

Однако использовать для тех же целей многочлен x⁴ + х³ + х² + x + 1 нельзя. При проверке числа различных остатков обнаруживается, что их у него не 15, а только 5 Действительно,

Это объясняется тем, что многочлен x⁴ + х³ + х² + x + 1 входит в разложение не только двучлена x¹⁵ + 1, но и двучлена х⁵ + 1.

Из приведенного примера следует, что в качестве образующего следует выбирать такой неприводимый многочлен g(x) (или произведение таких многочленов), который, являясь делителем двучлена хⁿ⁺¹, не входит в разложение ни одного двучлена типа x^ λ+1, степень которого λ меньше n. В этом случае говорят, что многочлен q(x) принадлежит показателю степени n.

В табл. 6.12 приведены основные характеристики некоторых кодов, способных исправлять одиночные ошибки или обнаруживать все одиночные и двойные ошибки.

Таблица 6.12

Это циклические коды Хэмминга для исправления одной ошибки, в которых в отличие от групповых кодов Хэмминга все проверочные разряды размещаются в конце кодовой комбинации.

Эти коды могут быть использованы для обнаружения любых двойных ошибок. Многочлен, соответствующий вектору двойной ошибки, имеет вид ξ(χ) = xⁱ + xⁱ, или ξ(x) = xⁱ(x^j-i + 1) при j>i. Так как j-i<n а g(x) не кратен x и принадлежит показателю степени n, то ξ(x) не делится на g(x), что и позволяет обнаружить двойные ошибки.

Обнаружение ошибок кратности три и ниже. Образующие многочлены кодов, способных обнаруживать одиночные, двойные и тройные ошибки, можно определить, базируясь на следующем указании Хэмминга. Если известен образующий многочлен p(x^m) кода длины n, позволяющего обнаруживать ошибки некоторой кратности z то образующий многочлен g(x) кода, способного обнаруживать ошибки следующей кратности (z+1), может быть получен умножением многочлена р(х^m) на многочлен x+1, что соответствует введению дополнительной проверки на четность. При этом число символов в комбинациях кода за счет добавления еще одного проверочного символа увеличивается до n + 1.

В табл. 6.13 приведены основные характеристики некоторых кодов, способных обнаруживать ошибки кратности три и менее.

Таблица 6.13

Обнаружение и исправление независимых ошибок произвольной кратности. Важнейшим классом кодов, используемых в каналах, где ошибки в последовательностях символов возникают независимо, являются коды Боуза — Чоудхури — Хоквингема. Доказано, что для любых целых положительных чисел m и s<n/2 существует двоичный код этого класса длины n = 2^m—1 с числом проверочных символов не более ms, который способен обнаруживать ошибки кратности 2s или исправлять ошибки кратности s. Для понимания теоретических аспектов этих кодов необходимо ознакомиться с рядом новых понятий высшей алгебры. Вопросы их построения и технической реализации рассмотрены в § 6.9. — Обнаружение и исправление пачек ошибок. Для произвольного линейного блокового (n, k)-кода, рассчитанного на исправление пакетов ошибок длины b или менее, основным соотношением, устанавливающим связь корректирующей способности с числом избыточных символов, является граница Рейджера:

При исправлении линейным кодом пакетов длины b или менее с одновременным обнаружением пакетов длины l>=b или менее требуется по крайней мере b + l проверочных символов.

Из циклических кодов, предназначенных для исправления пакетов ошибок, широко известны коды Бартона, Файра и Рида — Соломона.

Первые две разновидности кодов служат для исправления одного пакета ошибок в блоке. Коды Рида — Соломона способны исправлять несколько пачек ошибок.

Особенности декодирования циклических кодов, исправляющих пакеты ошибок, рассмотрены далее на примере кодов Файра.

Методы образования циклического кода. Существует несколько различных способов кодирования. Принципиально наиболее просто комбинации циклического кода можно получить, умножая многочлены а(х), соответствующие комбинациям безызбыточного кода (информационным символам), на образующий многочлен кода g(x). Такой способ легко реализуется. Однако он имеет тот существенный недостаток, что получающиеся в результате умножения комбинации кода не содержат информационные символы в явном виде. После исправления ошибок такие комбинации для выделения информационных символов приходится делить на образующий многочлен кода.

Применительно к циклическим кодам принято (хотя это и не обязательно) отводить под информационные k символов, соответствующих старшим степеням многочлена кода, а под проверочные n — k символов низших разрядов.

Чтобы получить такой систематический код, применяется следующая процедура кодирования.

Многочлен а(х), соответствующий k-разрядной комбинации безызбыточного кода, умножаем на х^m, где m = n — k. Степень каждого одночлена, входящего в а(х), увеличивается, что по отношению к комбинации кода означает необходимость приписать со стороны младших разрядов m нулей. Произведение а(х)х^m делим на образующий многочлен g(x). В общем случае при этом получаем некоторое частное q(x) той же степени, что и а(х) и остаток r(х). Последний прибавляем к а(х)х^m. В результате получаем многочлен

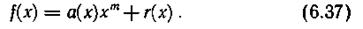
Поскольку степень g(x) выбираем равной m, степень остатка r(х) не превышает m — 1. В комбинации, соответствующей многочлену а(х)х^m, m младших разрядов нулевые, и, следовательно, указанная операция сложения равносильна приписыванию r(х) к а(х) со стороны младших разрядов.

Покажем, что f(x) делится на g(x) без остатка, т. е. является многочленом, соответствующим комбинации кода. Действительно, запишем многочлен а(х)х^m в виде

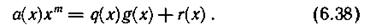
Так как операции сложения и вычитания по модулю два идентичны, r(х) можно перенести влево, тогда

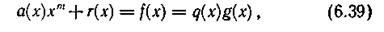
что и требовалось доказать.

Таким образом, циклический код можно строить, приписывая к каждой комбинации безызбыточного кода остаток от деления соответствующего этой комбинации многочлена на образующий многочлен кода. Для кодов, число информационных символов в которых больше числа проверочных, рассмотренный способ реализуется наиболее просто.

Следует указать еще на один способ кодирования. Так как циклический код является разновидностью группового кода, то его проверочные символы должны выражаться через суммы по модулю два определенных информационных символов.

Равенства для определения проверочных символов могут быть получены путем решения рекуррентных соотношений:

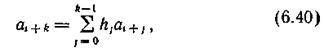
где h — двоичные коэффициенты так называемого генераторного многочлена h(x), определяемого так

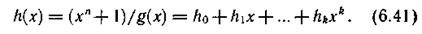
Соотношение (6.40) позволяет по заданной последовательности информационных сигналов a₀, a₁,..., a_k-1, вычислить n — k проверочных символов a_k, a_k+1,...,а_n-1. Проверочные символы, как и ранее, размещаются на местах младших разрядов. При одних и тех же информационных символах комбинации кода, получающиеся таким путем, полностью совпадают с комбинациями, получающимися при использовании предыдущего способа кодирования. Применение данного способа целесообразно для кодов с числом проверочных символов, превышающим число информационных, например, для кодов Боуза — Чоудхури — Хоквингема.

Матричная запись циклического кода. Полная образующая матрица циклического кода Mn,k составляется из двух матриц: единичной I_k (соответствующей k информационным разрядам) и дополнительной C_k,n-k (соответствующей проверочным разрядам):

Построение матрицы I_k трудностей не представляет.

Если образование циклического кода производится на основе решения рекуррентных соотношений, то его дополнительную матрицу можно определить, воспользовавшись правилами, указанными ранее. Однако обычно строки дополнительной матрицы циклического кода C_k,n-k определяются путем вычисления многочленов r(х). Для каждой строки матрицы Ik соответствующий r(х) находят делением информационного многочлена а(х)х^m этой строки на образующий многочлен кода g(x).

Дополнительную матрицу можно определить и не строя I_k. Для этого достаточно делить на g(x) комбинацию в виде единицы с рядом нулей и получающиеся остатки записывать в качестве строк дополнительной матрицы. При этом если степень какого-либо r(х) оказывается меньше n — k— 1, то следующие за этим остатком строки матрицы получают путем циклического сдвига предыдущей строки влево до тех пор, пока степень r(х) не станет равной n — k—1. Деление производится до получения k строк дополнительной матрицы.

Пример 6.14. Запишем образующую матрицу для циклического кода (15,11) с порождающим многочленом g(x) = x⁴ + x³ + 1 ·

Воспользовавшись результатами ранее проведенного деления, получим

Существует другой способ построения образующей матрицы, базирующийся на основной особенности циклического (n, k)-кода (см § 6.6). Он проще описанного, но получающаяся матрица менее удобна.

Матричная запись кодов достаточно широко распространена.

Укороченные циклические коды. Корректирующие возможности циклических кодов определяются степенью m образующего многочлена. В то время как необходимое число информационных символов может быть любым целым числом, возможности в выборе разрядности кода весьма ограничены.

Если, например, необходимо исправить единичные ошибки при k = 5, то нельзя взять образующий многочлен третьей степени, поскольку он даст только семь остатков, а общее число разрядов получится равным 8.

Следовательно, необходимо брать многочлен четвертой степени и тогда n= 15. Такой код рассчитан на 11 информационных разрядов.

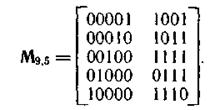
Однако можно построить код минимальной разрядности, заменив в (n, k) -коде j первых информационных символов нулями и исключив их из кодовых комбинаций. Код уже не будет циклическим, поскольку циклический сдвиг одной разрешенной кодовой комбинации не всегда приводит к другой разрешенной комбинации того же кода. Получаемый таким путем линейный (n — j, k — j)-код называют укороченным циклическим кодом. Минимальное расстояние этого кода не менее, чем минимальное кодовое расстояние (n, k)-кода, из которого он получен. Матрица укороченного кода получается из образующей матрицы (n, k)-кода исключением j строк и столбцов, соответствующих старшим разрядам. Например, образующая матрица кода (9,5), полученная из матрицы кода (15,11), имеет вид

§ 6.8 ТЕХНИЧЕСКИЕ СРЕДСТВА КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДЛЯ ЦИКЛИЧЕСКИХ КОДОВ

Линейные переключательные схемы. Основу кодирующих и декодирующих устройств циклических кодов составляют регистры сдвига с обратными связями, позволяющие осуществлять как умножение, так и деление многочленов с приведением коэффициентов по модулю два. Такие регистры также называют многотактными линейными переключательными схемами и линейными кодовыми фильтрами Хаффмена. Они состоят из ячеек памяти, сумматоров по модулю два и устройств умножения на коэффициенты многочленов множителя или делителя. В случае двоичных кодов для умножения на коэффициент, равный 1, требуется только наличие связи в схеме. Если коэффициент равен 0, то связь отсутствует. Сдвиг информации в регистре осуществляется импульсами, поступающими с генератора продвигающих импульсов, который на схеме, как правило, не указывается. На вход устройств поступают только коэффициенты многочленов, причем начиная с коэффициента при переменной в старшей степени.

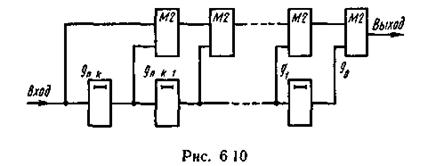На рис. 6.10 представлена схема, выполняющая умножение произвольного (например, информационного) многочлена а(х)g(x) = а₀+а₁х+...+a_k-1*x^k-1 на некоторый фиксированный (например, образующий) многочлен g(х)=g₀+g₁ +...+g_n-k*x^n-k. Произведение этих многочленов равно

Предполагаем, что первоначально ячейки памяти находятся в нулевом состоянии и что за коэффициентами множимого следует n — k нулей.

На первом такте на вход схемы поступает первый коэффициент a_k-1 многочлена а(х) и на выходе появляется первый коэффициент произведения, равный а_k-1,g_n-k. На следующем такте на выход поступит сумма a_k-2 g_n-k+a_k-1g_n-k-1, т.е. второй коэффициент произведения, и т. д. На n-м такте все ячейки, кроме последней, будут в нулевом состоянии и на выходе получим последний коэффициент a₀g₀.

Используется также схема умножения многочленов при поступлении множимого младшим разрядом вперед (рис. 6.11).

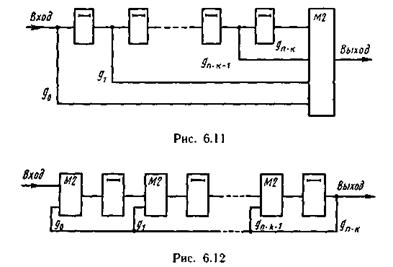На рис. 6.12 представлена схема, выполняющая деление произвольного многочлена [например, многочлена ι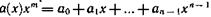] на некоторый фиксированный (например, образующий) многочлен g(x) = g₀+g₁x+...+g_n-k*x^n-k. Обратные связи регистра соответствуют виду многочлена g(x). Количество включаемых в него сумматоров равно числу отличных от нуля коэффициентов g(x), уменьшенному на единицу. Это объясняется тем, что сумматор сложения коэффициентов старших разрядов многочленов делимого и делителя в регистр не включается, так как результат сложения заранее известен (он равен 0).

За первые n — k тактов коэффициенты многочлена-делимого заполняют регистр, причем коэффициент при x в старшей степени достигает крайней правой ячейки. На следующем такте «единица» делимого, выходящая из крайней ячейки регистра, по цепи обратной связи подается к сумматорам по модулю два, что равносильно вычитанию многочлена-делителя из многочлена-делимого. Если в результате предыдущей операции коэффициент при старшей степени x у остатка оказался равным нулю, то на следующем такте делитель не вычитается. Коэффициенты делимого только сдвигаются вперед по регистру на один разряд, что находится в полном соответствии с тем, как это делается при делении многочленов столбиком.

Деление заканчивается с приходом последнего символа многочлена-делимого. При этом разность будет иметь более низкую степень, чем делитель. Эта разность и есть остаток.

Отметим, что если в качестве многочлена-делителя выбран простой многочлен степени m = n — k, то, продолжая делить образовавшийся остаток при отключенном входе, будем получать в регистре по одному разу каждое из ненулевых m-разрядных двоичных чисел. Затем эта последовательность чисел повторяется.

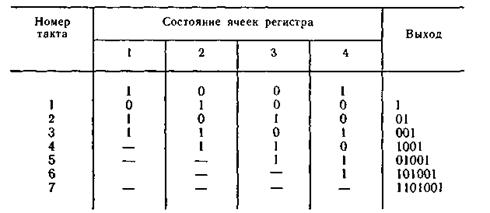
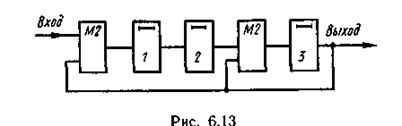Пример 6.15. Рассмотрим процесс деления многочлена а(х)х^m= (x^3+1)x^3 на образующий многочлен g(x) = x^3 + + x^2 + 1. Схема для этого случая представлена на рис. 6.13, где 1, 2, 3 — ячейки регистра. Работа схемы поясняется табл. 6.14.

Таблица 6.14

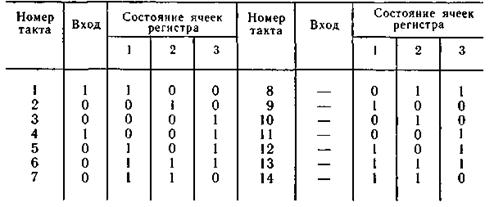
Вычисление остатка начинается с четвертого такта и заканчивается после седьмого такта. Последующие сдвиги приводят к образованию в регистре последовательности из семи различных ненулевых трехразрядных чисел. В дальнейшем эта последовательность чисел повторяется.

Рассмотренные выше схемы умножения и деления многочленов непосредственно в том виде, в каком они представлены на рис. 6.11, 6.12, в качестве кодирующих устройств циклических кодов на практике не применяются: первая — из-за того, что образующаяся кодовая комбинация в явном виде не содержит информационных символов, а вторая — из-за того, что между информационными и проверочными символами образуется разрыв в n — k разрядов.

Кодирующие устройства. Все известные кодирующие устройства для любых типов циклических кодов, выполненные на регистрах сдвига, можно свести к двум типам схем согласно рассмотренным ранее методам кодирования.

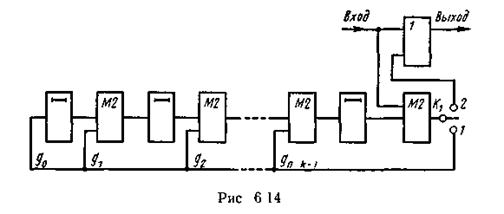Схемы первого типа вычисляют значения проверочных символов путем непосредственного деления многочлена а(х)х^m на образующий многочлен g(x). Это делается с помощью регистра сдвига, содержащего n — k разрядов (рис. 6.14). Схема отличается от ранее рассмотренной тем, что коэффициенты кодируемого многочлена участвуют в обратной связи не через n — k сдвигов, а сразу с первого такта. Это позволяет устранить разрыв между информационными и проверочными символами

В исходном состоянии ключ К1 находится в положении 1. Информационные символы одновременно поступают как в линию связи, так и в регистр сдвига, где за k тактов образуется остаток. Затем ключ Κ1 переходит в положение 2 и остаток поступает в линию связи.

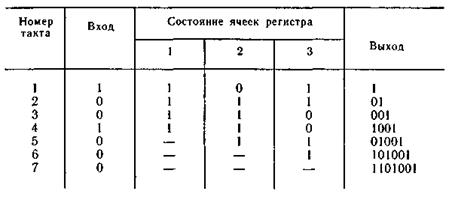
Пример 6.16. Рассмотрим процесс деления многочлена а(х)х^m = = (х³ + +1)x³ на многочлен g(x) = x³ + x²+ 1 за k тактов

Схема кодирующего устройства для заданного g(x) приведена на рис 6.15 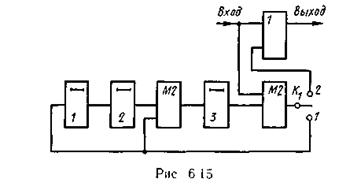Процесс формирования кодовой комбинации шаг за шагом представлен в табл. 6.15, где черточками отмечены освобождающиеся ячейки, занимаемые новыми информационными символами.

Таблица 6.15.

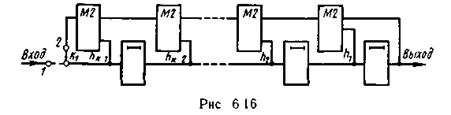С помощью схем второго типа вычисляют значения проверочных символов как линейную комбинацию информационных символов, т. е они построены на использовании основного свойства систематических кодов Кодирующее устройство строится на основе k-разрядного регистра сдвига (рис 6.16) Выходы ячеек памяти подключаются к сумматору в цепи обратной связи в соответствии с видом генераторного многочлена

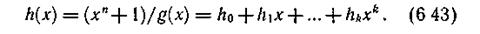
В исходном положении ключ Κ1 находится в положении 1. За первые k тактов поступающие на вход информационные символы заполняют все ячейки регистра. После этого ключ переводят в положение 2. На каждом из последующих тактов один из информационных символов выдается в канал связи и одновременно формируется проверочный символ, который записывается в последнюю ячейку регистра. Через n — k тактов процесс формирования проверочных символов заканчивается и ключ Κ1 снова переводится в положение 1.

В течение последующих k тактов содержимое регистра выдается в канал связи с одновременным заполнением ячеек новой последовательности информационных символов.

Пример 6.17. Рассмотрим процесс формирования кодовой комбинации с использованием генераторного многочлена для случая g(x) = = х³ + х² + 1 и а(х) = =х³+1

Определяем генераторный многочлен.

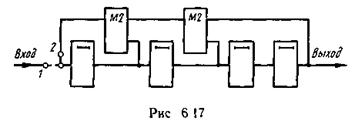Соответствующая h(x) схема кодирующего устройства приведена на рис. 6.17. Формирование кодовой комбинации поясняется табл. 6.16. Оно начинается после заполнения регистра информационными символами.

Таблица 6.16

Декодирующие устройства. Декодирование комбинаций циклического кода можно проводить различными методами. Существуют методы, основанные на использовании рекуррентных соотношений, на мажоритарном принципе, на вычислении остатка от деления принятой комбинации на образующий многочлен кода и др. Целесообразность применения каждого из них зависит от конкретных характеристик используемого кода.

Рассмотрим сначала устройства декодирования, в которых для обнаружения и исправления ошибок производится деление произвольного многочлена f(x), соответствующего принятой комбинации, на образующий многочлен кода go(x). В этом случае при декодировании могут использоваться те же регистры сдвига, что и при кодировании.

Декодирующие устройства для кодов, обнаруживающих ошибки, по существу ничем не отличаются от схем кодирующих устройств. В них добавляется лишь буферный регистр для хранения принятого сообщения на время проведения операции деления. Если остатка не обнаружено (случай отсутствия ошибки), то

информация с буферного регистра считывается в дешифратор сообщения. Если остаток обнаружен (случай наличия ошибки), то информация в буферном регистре уничтожается и на передающую сторону посылается импульс запроса повторной передачи.

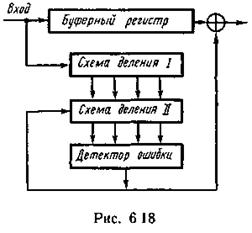В случае исправления ошибок схема несколько усложняется. Информацию о разрядах, в которых произошла ошибка, несет, как и ранее, остаток. Схема декодирующего устройства представлена на рис. 6.18.

Символы подлежащей декодированию кодовой комбинации, возможно, содержащей ошибку, последовательно, начиная со старшего разряда, вводятся в n-разрядный буферный регистр сдвига и одновременно в схему деления, где за n тактов определяется остаток, который в случае непрерывной передачи сразу же переписывается в регистр второй аналогичной схемы деления.

Начиная с (n + 1)-го такта в буферный регистр и первую схему деления начинают поступать символы следующей кодовой комбинации. Одновременно на каждом такте буферный регистр покидает один символ, а в регистре второй схемы деления появляется новый остаток (синдром). Детектор ошибок, контролирующий состояния ячеек этого регистра, представляет собой комбинаторно-логическую схему, построенную с таким расчетом, чтобы она отмечала все те синдромы («выделенные синдромы»), которые появляются в схеме деления, когда каждый из ошибочных символов занимает крайнюю правую ячейку в буферном регистре. При последующем сдвиге детектор формирует сигнал «1», который, воздействуя на сумматор коррекции, исправляет искаженный символ.

Одновременно по цепи обратной связи с выхода детектора подается сигнал «1» на входной сумматор регистра второй схемы деления. Этот сигнал изменяет выделенный синдром так, чтобы он снова соответствовал более простому типу ошибки, которую еще подлежит исправить. Продолжая сдвиги, обнаружим и другие выделенные синдромы. После исправления последней ошибки все ячейки декодирующего регистра должны оказаться в нулевом состоянии. Если в результате автономных сдвигов состояние регистра не окажется нулевым, это означает, что произошла неисправимая ошибка.

Для декодирования кодовых комбинаций, разнесенных во времени, достаточно одной схемы деления, осуществляющей декодирование за 2n тактов.

Сложность детектора ошибок зависит от числа выделенных синдромом. Простейшие детекторы получаются при реализации кодов, рассчитанных на исправление единичных ошибок.

Выделенный синдром появляется в схеме деления раньше всего в случае, когда ошибка имеет место в старшем разряде кодовой комбинации, так как он первым достигает крайней правой ячейки буферного регистра. Поскольку неискаженная кодовая комбинация делится на g₀(x) без остатка, то для определения выделенного синдрома достаточно разделить на g₀(x) вектор ошибки с единицей в старшем разряде. Остаток, получающийся на n-м такте, и является искомым выделенным синдромом.

В зависимости от номера искаженного разряда после первых тактов будем получать различные остатки (опознаватели соответствующих векторов ошибок). Вследствие этого выделенный синдром будет появляться в регистре схемы деления через различное число последующих тактов, обеспечивая исправление искаженного символа.

В качестве схем деления в декодирующем устройстве могут быть использованы как схемы, определяющие остаток за n тактов (см. рис. 6.12), так и схемы, определяющие остаток за k тактов (рис. 6.14). При использовании схемы деления за k тактов векторам одиночных ошибок ξ(x) будут соответствовать другие остатки на n-м такте, являющиеся результатом деления на образующий многочлен кода векторов ξ(x)x^m, а не ξ(x). Поэтому выделенные синдромы, а следовательно, и детекторы ошибок для указанных схем будут различны.

Пример 6.18. Рассмотрим процесс исправления единичной ошибки при использовании кода (7,4) с образующим многочленом g(x) = х³ + x² + 1 и применении в декодирующем устройстве схем деления за n и k тактов.

Определим опознаватели ошибок и выделенный синдром для случая использования схемы деления за n тактов:

Дата добавления: 2014-10-23