Растяжение (сжатие)

Этот вид деформации возникает, когда к стержню (бруску) с закрепленным основанием прикладывается сила F, направленная вдоль его оси (рис. 6.1, а). Под действием этой силы длина стержня увеличивается на некоторую величину Δ l (l - первоначальная длина).

При этом в каждом сечении стержня возникают направленные по нормали силы (F₁ и F₂), равные по величине приложенной силе F и обусловленные изменением расстояния между частицами при растяжении. Сила F₁ действует на верхнюю часть бруска со стороны нижней части; сила F₂ - наоборот (рис. 6.1, б).

Состояние растянутого тела характеризуется продольным (нормальным) напряжением σ, которое может быть вычислено для любого сечения тела, перпендикулярного приложенной силе.

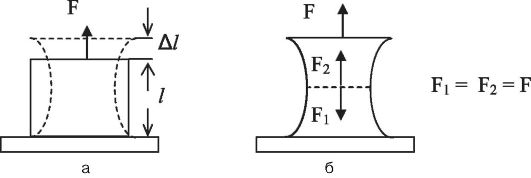Рис. 6.1. Деформация растяжения (а); силы, возникающие при растяжении (б)

Нормальное напряжение равно отношению модуля силы, возникающей в данном сечении в результате растяжения, к площади сечения:

В СИ механическое напряжение измеряется в паскалях (Па).

Величина абсолютной деформации А! зависит от первоначальной длины стержня, поэтому степень деформации выражают через отношение абсолютной деформации к первоначальной длине. Это отношение называется относительной деформацией (ε):

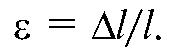Относительная деформация - величина безразмерная. Иногда ее выражают в процентах: ε = (Δ l / l)х100%.

В большинстве случаев при растяжении или сжатии степень деформации в различных сечениях стержня различна. Это можно увидеть, если на поверхность тела нанести квадратную сетку. После деформирования сетка исказится. По характеру и величине этого искажения можно судить о распределении напряжения вдоль образца (рис. 6.2).

Видно, что изменения формы ячеек сетки максимальны в средней части стержня и почти отсутствуют на его краях.

Опытным путем было установлено, что небольшие деформации исчезают после снятия внешнего воздействия. Такие деформации называются упругими. Для них выполняется закон Гука:

При упругой деформации напряжение прямо пропорционально величине относительной деформации:

Коэффициент пропорциональности Е характеризует упругие свойства вещества при растяжении (сжатии) и называется модулем Юнга (модуль продольной упругости, Па). В таблице 6.1 представлены значения модулей упругости некоторых материалов.

Рис. 6.2. Искажение квадратной сетки при растяжении стержня

Дата добавления: 2014-10-23