Модель Кельвина-Фойгта

Механические модели деформации биологических сред (модель Максвелла)

Вязкоупругие свойства тел (сочетание вязкого течения и высокой эластичности) моделируются системами, состоящими из различных комбинаций двух простых элементов: 1) пружины (упругий элемент) и 2) поршня с отверстиями, движущегося в цилиндре с вязкой жидкостью (вязкий элемент). Эти элементы и «конструируемые» с их помощью модели показаны на рис. 6.19 слева. Справа показаны зависимости деформации (ε) от времени при импульсном воздействии внешней силы: в момент времени t = 0 к телу, поведение которого моделируется, прикладывается постоянная сила F; в момент времени t₁ действие силы прекращается.

Моделью упругого тела является пружина (рис. 6.19, а), подчиняющаяся закону Гука. Деформация (ε) мгновенно появляется в момент t = 0 и мгновенно исчезает в момент t₁.

Моделью вязкого тела является поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью (рис. 6.19, б). Связь между скоростью деформации вязкой среды (скоростью перемещения поршня) и напряжением имеет вид

Модель Максвелла

В модели Максвелла упругий и вязкий элементы соединены последовательно (рис. 6.19, в). Напряжение в каждом элементе является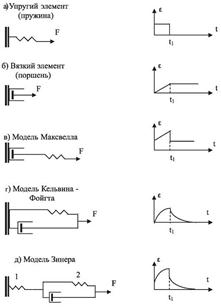 Рис. 6.19. Механические модели вязкоупругих тел и динамика развития деформации

одинаковым. В любой момент времени для деформации выполняется условие

Решение этого уравнения приводит к следующему характеру развития деформации. В момент t = 0 пружина мгновенно растягивается, а затем начинается линейное нарастание деформации, связанное с движением поршня. В момент t₁ пружина сокращается до начального размера, а поршень останавливается - имеет место остаточная деформация.

С помощью модели Максвелла можно моделировать следующие механические процессы.

Релаксация напряжения в материале: ε = const, dε/dt = 0, т.е. поддерживается постоянная деформация. В этом случае из уравнения (6.10) следует

Интегрируя последнее выражение от начального момента времени и начального напряжения σ _о до текущих значений t иσ, получаем выражение, описывающее изменение напряжения со временем, т.е. релаксацию напряжения:

т.е. под действием постоянной приложенной силы происходит вязкое течение (поршень движется с постоянной скоростью).

При изучении свойств волос используют явление релаксации напряжения в них. Этот процесс аппроксимируют моделью, состоящей из 4 параллельно соединенных моделей Максвелла.

Модель Максвелла не учитывает упругости, отличной от той, которая подчиняется закону Гука, т.е. упругости, возникающей за счет раскручивания макромолекул (высокоэластичности). Основной особенностью этого вида упругости является необходимость известного промежутка времени для ее развития (аналогия - деформация пружины в вязкой среде). Такая «запаздывающая» упругая реакция представляется моделью Кельвина-Фойгта, в которой пружина и поршень соединены параллельно (рис. 6.19, г). Величина удлинения одинакова для обоих элементов. При воздействии внешней силы общее напряже-

Модель Зинера

В материалах реализуются разные виды деформаций: упругая обратимая (модель - пружина), вязкоупругая обратимая (модель Кельвина-Фойгта) и необратимая (модель - поршень). Сочетание трех моделей, рассмотренных выше, позволяет создавать модели, наиболее полно отражающие механические свойства тел и, в частности, биологических объектов.

Примером такой модели является модель Зинера (рис. 6.19, д), которая состоит из последовательно соединенных упругого элемента и модели Кельвина-Фойгта. Временная зависимость относительной

деформации (без вывода) показана на рис. 6.19, д. При действии постоянной нагрузки мгновенно растягивается пружина 1, затем вытягивается поршень и растягивается пружина 2, после прекращения нагрузки происходит быстрое сжатие пружины 1, а пружина 2 втягивает поршень в прежнее положение; остаточная деформация отсутствует.

Поведение костной ткани в первом приближении описывается моделью Зинера. Упругая деформация реализуется за счет минерального вещества, а ползучесть - за счет коллагена.

Продолжение таблицы

Дата добавления: 2014-10-23