Собственные функции и собственные значения. Свободная частица

Функции Y,удовлетворяющие уравнению Шредингера при данных U, называются собственными функциями.

Значения Е, при которых существуют решения уравнения (22), называются собственными значениями.

В качестве примера определим y и Е для свободной частицы.

Свободной называют частицу, на которую не действуют силы, т.е. . Следовательно, U(x)=const и ее можно принять равной нулю. Таким образом, в случае свободного движения частицы, ее полная энергия совпадает с кинетической, а скорость 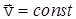. Направим ось Х вдоль вектора 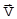. Тогда (22) можно записать в виде

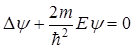. (23)

Прямой подстановкой можно убедится, что частным решением этого уравнения является функция y(х)=Аexp(ikx), где А=сonst, k=const c собственным значением энергии

Е=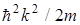. (24)

C учетом (21) волновая функция

Y(х)=Аexp(-iwt+ ikx)= Аexp[-(i/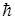)(Еt- р_xх)]. (25)

здесь w=Е/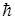, k=р_x/.

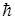Функция (25) представляет собой плоскую монохроматическую волну де Бройля [cм. (16)].

Из (24) следует, что зависимость энергии от импульса

Е=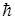²k²/(2m)=Р_х²/(2m)=m v ²/2 (26)

оказывается обычной для нерелятивиских частиц. Следовательно, энергия свободной частицы может принимать любые значения, т.е. ее энергетический спектр является непрерывным.

Плотность вероятности обнаружить частицу в данной точке пространства

çy÷ ²=yy^*=A²,

т.е. все положения свободной частицы в пространстве являются равновероятными.

9.6. Частица в одномерной прямоугольной «потенциальной яме»

Такая «яма» описывается потенциальной энергией вида

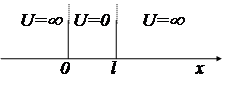
При таком условии частица не проникает за

пределы "ямы", т.е. y(0)= y(l)=0. (27)

В пределах ямы (0<x<l) уравнение (22) сведется к уравнению

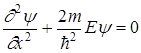или 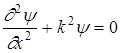, (28)

где k²=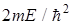. Общее решение (28) y(х)=Аsinkx+Bcoskx. (29)

Так как согласно (27) ψ(0)=0, то В= 0, тогда y(х)=Аsinkx. (30)

Условие (27) y(l)=Аsinkl=0 выполняется только при kl=pn, где n=1,2... целые числа, т.е. необходимо, чтобы k=pn/l. (31)

Из (29) и (31) следует, что (32)

Таким образом, энергия в «потенциальной яме» принимает лишь определенные, дискретные значения, т.е. квантуется. Квантованные значения энергии Е_n называются уровнями энергии, а число n, определяющее энергетические уровни, называется главным квантовым числом.

Заметим, что n=1 cоответствует минимальная энергия Е₁¹0.

Подставив в (30) значения k из (31), найдем собственные функции

.

Постоянную А найдем из условия нормировки (18), которое для данного случая имеет вид

.

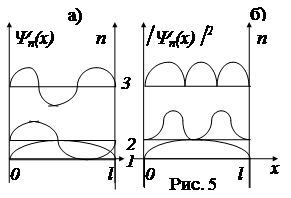В результате интегрирования получим , а собственные функции будут иметь вид

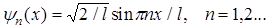(33)

Графики этих функций, соответствующие уровням энергии при n= 1, 2, 3, приведены на рис. 5 (а). На рис. 5 (б) изображены плотности вероятности обнаружения частицы на различных расстояниях от «стенок» ямы

Из рис. следует, что, например, в квантовом состоянии с n= 2 частица не может находится в середине «ямы», в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы указывает на то, что представления о траектории частицы в квантовой механике несостоятельны.

Дата добавления: 2014-10-23