Напряженность электрического поля внутри конденсатора

Лекция 26. Закон изменения напряжения на обкладках конденсатора

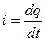; (24.1)

; (24.2)

I₀=const; (24.3)

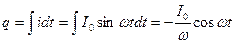; (24.4)

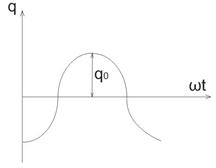
Рис. 24.1 – Заряд на обкладках конденсатора

Вывод: заряд на обкладках конденсатора изменяется также как i и u, т.е. по гармоническому закону.

, (24.5)

где - поверхностная плотность заряда;

q – заряд на обкладках конденсатора;

S – площадь обкладок конденсатора.

То есть

(24.6)

между обкладками конденсатора существует переменное электрическое поле и согласно гипотезе Максвелла, между обкладками конденсатора (где нет проводников) протекают токи смещения. Эти токи смещения и возбуждают между обкладками конденсатора переменное магнитное поле. Найдем связь между этими полями: электрическим и магнитным.

Переменное электрическое поле в конденсаторе в каждый момент времени создает такое переменное магнитное поле, как если бы между обкладками конденсатора существовал ток проводимости (i) равный по силе току смещения (I_смещ) в подводящих проводах, т.е. i=i_смещ. Откуда следует, что j=j_смещ. Где j – плотность тока проводимости; j – плотность тока смещения.

; (24.7)

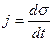. (24.8)

В конденсаторе:

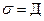, (24.9)

где Д – электрическое смещение;

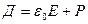, (24.10)

где 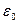- электрическая постоянная,

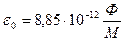; (24.11)

Е – напряженность электрического поля;

Р – абсолютное значение вектора поляризации (или поляризуемость);

. (24.12)

В данном уравнении знак частной производной указывает на то, что магнитное поле определяется лишь скоростью изменения Д по времени t.

Рассмотрим, как направлены j, j_смещ и Д.

Можно показать, что всегда при зарядке и разряде конденсатора, векторы j, j_смещ; 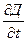- совпадают, поэтому можно представить в виде: 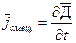. (24.13)

В диэлектрике:

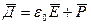; (24.15)

Получаем

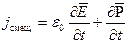, (24.16)

где - плотность тока i_смещ в вакууме;

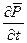- плотность потока поляризации.

Вывод: из последнего уравнения следует, что даже в вакууме всякое изменение во времени электрического поля, приводит к возникновению в открытом пространстве магнитного поля, т.к. магнитное поле возникает при любом изменении электрического поля, то i_смещ существует и в проводниках, но i_смещ<<i.

Развивая свою теорию Максвелл ввел понятие полного тока:

i_полн=i+i_смещ, (24.17)

, (24.18)

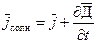, (24.19)

где 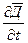- плотность тока смещения.

Полный ток в цепях переменного тока всегда замкнут.

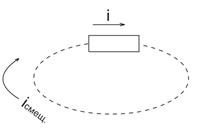
Рис. 24.2 - Полный ток в цепи переменного тока

Вывод: обрывается лишь ток проводимости, а в диэлектрике или в вакууме между концами проводника имеется ток смещения, который и замыкает ток проводимости. Используя понятие полного тока Максвелл обобщил теорему о циркуляции . Для этого выражение полного тока было представлено в виде:

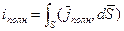. (24.20)

Пусть полный ток i_полн охватывается контуром L, тогда:

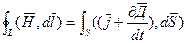(24.21)

- обобщенная теорема о циркуляции вектора Н (закон полного тока).

Дата добавления: 2014-10-23